exemplo 01

Escreva a equação vetorial para $y=5x+3$ no plano $z=2$
SOL.
Seja \[ \begin{align*} x(t) =& t\\ y(t) =& 5t+3\\ z(t) =& 2 \end{align*} \] assim \[ \mathbf{r}(t) = t \,\mathbf{i} + \left( 5t+3\right) \,\mathbf{j}+ 2 \,\mathbf{k} \nonumber \]

exemplo 02

A interseção da superfície $z=x^2+y^2$ e $z=2+y$ determina uma curva, encontre a equação vetorial dessa curva.
SOL.
\[ \begin{align*} 2+y =& x^2 + y^2\\ x^2 + y^2 -y+ \dfrac{1}{4} =& 2 - \dfrac{1}{4}\\ x^2 + \left( y-\dfrac{1}{2}\right)^2=& \dfrac{9}{4} \end{align*} \] então obtemos uma circunferência com centro em $\left(0,2\right)$ e raio $3/2$, por tanto a parametrização é \[ \begin{align*} x =& \dfrac{3}{2}\cos\,t\\ y =& \dfrac{1}{2} + \dfrac{3}{2}\sin\,t\\ z =& 2 + y\\ =& 2 + \dfrac{1}{2} + \dfrac{3}{2}\sin\,t\\ =& \dfrac{5}{2} + \dfrac{3}{2}\sin\,t\\ \end{align*} \]

Exemplo 3

Representar parametricamente a curva dada pela interseção das superfícies $x+y=2$ e $x^2+y^2+z^2=2(x+y)$
SOL.
Como $x+y=2\Rightarrow x = 2-y$, substituímos na segunda equação \[ \begin{align*} x^2+y^2+z^2=& 2(x+y)\\ \left(2-y \right)^2 + y^2 + z^2 =& 2\left(2-y +y \right)\\ 4-4y+y^{2}+y^{2}+z^{2}=&4\\ 2y^{2}-4y+z^{2}=&0\\ y^{2}-2y+1+\dfrac {z^{2}} {2}=&1\\ \left( y-1\right) ^{2}+\dfrac {z^{2}} {2}=&1 \end{align*} \] onde temos uma elipse no plano yz, assim as componentes estão dadas por \[ \begin{align*} y=&1+\cos t\\ z=&\sqrt{2}\sin t\\ x =& 1-\cos t \end{align*} \]

Exemplo 04

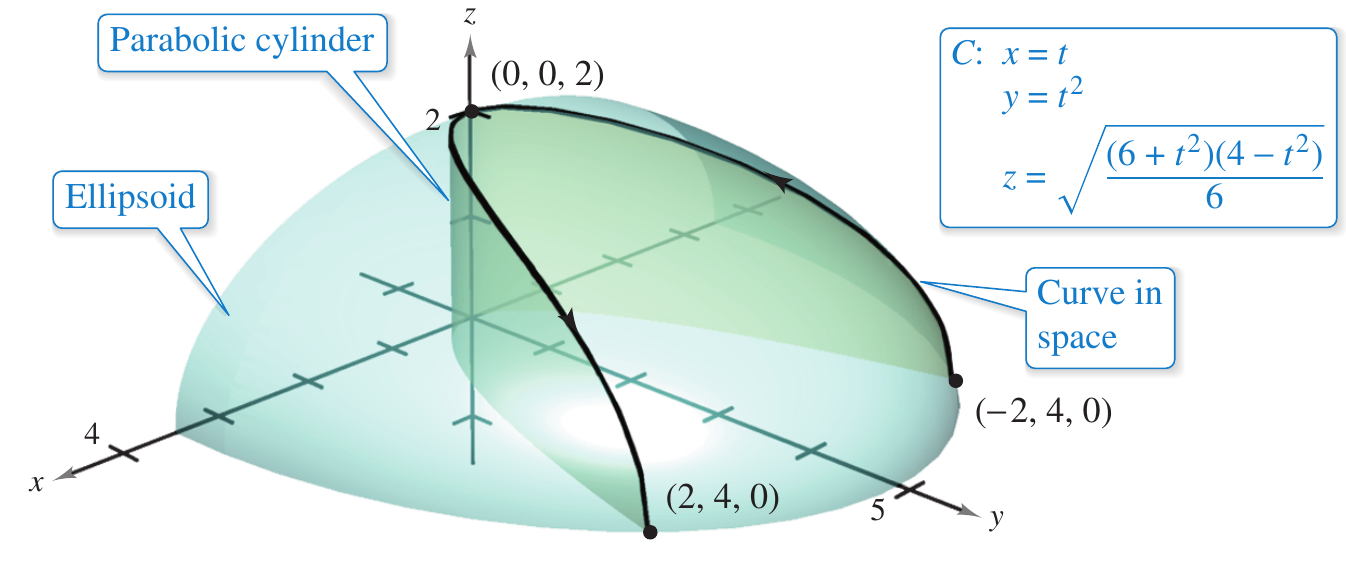
Esboce a curva obtida pela interseção do semi elipsoide \[ \dfrac {x^{2}} {12}+\dfrac {y^{2}} {24}+\dfrac {z^{2}} {4}=1,\;\;\;\;z\geq 0 \nonumber \] e o cilindro parabólico $\displaystyle y=x^2$. Encontre a função vetorial que descreve a curva
SOL.
A interseção das duas superfícies é mostrada na figura a seguir

A escolha de $t=x$ como parâmetro é uma opção adequada, assim o cilindro parabólico fica $\displaystyle y=t^2$. Agora vamos isolar $z$ da equação do elipsoide e substituímos $\displaystyle y=t^2$ e $t=x$ dentro dessa equação \[ \begin{align*} \dfrac {z^{2}} {4} =& 1-\dfrac {x^{2}} {12}-\dfrac {y^{2}} {24}\\ =& 1-\dfrac {t^{2}} {12}-\dfrac {t^{4}} {24}\\ =& \dfrac {24-2t^{2}-t^{4}} {24}\\ =& \dfrac {\left( 6+t^{2}\right) \left( 4-t^{2}\right) } {24} \end{align*} \] dessa forma as equações paramétricas que descrevem a curva são \[ \begin{align*} x =& t\\ y =& t^2\\ z =& \sqrt{\dfrac {\left( 6+t^{2}\right) \left( 4-t^{2}\right) } {6}} \end{align*} \] observe que escolhemos a solução positiva da raiz quadrada pois uma das condições do problema é que $z>0$.

Para saber os limites do parâmetro observamos que quando o elipsoide corta o plano $xy$ o valor de $z=0$, por tanto a figura projetada nesse plano está dada por \[ \begin{align*} \dfrac {x^{2}} {12}+\dfrac {y^{2}} {24}=&1\\ x^2 =& 12 - \dfrac {y^{2}} {2} \end{align*} \] igualando $x^2=y$ (equação do paraboloide) a fim de determinar a interseção das curvas no plano, teremos \[ \begin{align*} y =& 12 - \dfrac {y^{2}} {2}\\ y^2 + 2y + 1 =& 25\\ (y + 1)^2 =& 25\\ y+1 =& \pm 5\\ y_1 =& 4\\ y_2 =& -6 \end{align*} \] Note que a solução $y_2 = -6$ não faz sentido já que a equação do paraboloide limita os valores de $y$ tais que $y>0$. Como $y = t^2$, então temos que $t=\pm 2$, assim a equação vetorial da curva é \[ \mathbf{r}(t) = t\,\mathbf{i} +t^2 \,\mathbf{j} + \sqrt{\dfrac {\left( 6+t^{2}\right) \left( 4-t^{2}\right) } {6}} \,\mathbf{k}\;\;\;\;-2\leq t \leq 2 \nonumber \]

Exemplo 05

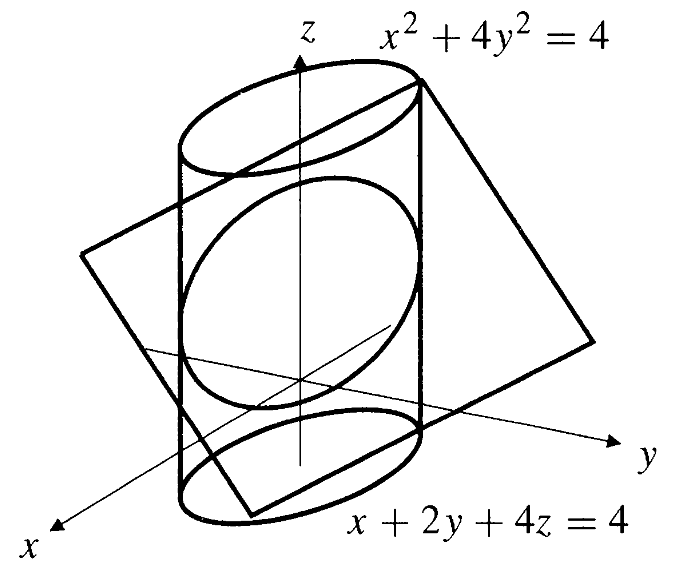
Parametrize a curva resultante da interseção do plano $x+2y+4z=4$ e o cilindro elítico $x^2 + 4y^2=4$
SOL.
A interseção das duas superfícies é mostrada na figura a seguir

Similar ao exemplo anterior, a parametrização pode ser realizada de varias forma, com temos um cilindro elítico a parametrização deste é exatamente igual à parametrização da elipse que resulta no plano perpendicular à geratriz, neste caso a elipse está dada por \[ \dfrac {x^{2}} {4}+\dfrac {y^{2}} {1}=1 \nonumber \] de onde a parametrização é \[ \begin{align*} x =& 2\cos\,t\\ y =& \sin\,t \end{align*} \] Agora vamos escrever a equação do plano utilizando essa parametrização, isolando $z$ \[ \begin{align*} z =& \dfrac {1} {4}\left( 4-x-2y\right) \\ =&1-\dfrac {1}{2}(\cos t+\sin t) \end{align*} \] de onde temos as equações paramétricas da curva desejada \[ \begin{align*} x =& 2\cos\,t\\ y =& \sin\,t\\ z =& 1-\dfrac {1}{2}(\cos t+\sin t) \end{align*} \] onde $0\leq t \leq 2\pi$