Exemplo 03

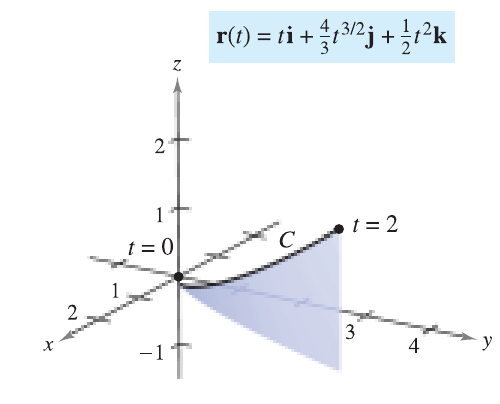
Encontre o comprimento arco da curva dada por $\mathbf{r}(t) = t \,\mathbf{i} + \dfrac{4}{3}t^{3/2}\,\mathbf{j} + \dfrac{1}{2}t^{2} \,\mathbf{k}$ entre $t=0$ e $t=2$.
SOL.
Da definição da função $\mathbf{r}(t)$ identificamos as funções componentes e calculamos suas derivas: \[ \begin{eqnarray*} x'(t) &=& 1\\ y'(t) &=& 2t^{1/2}\\ z'(t) &=& t \end{eqnarray*} \] dessa forma \[ \begin{eqnarray*} L &=& \int_0^2 \sqrt{\left( 1 \right)^2 + \left( 2t^{1/2} \right)^2 + \left( t\right)^2}\,\,\,\,dt\\ &=& \int_0^2 \sqrt{1 + 4t + t^2}\,\,dt\\ &=& \int_0^2 \sqrt{(t+2)^2 -3}\,\,dt\\ \end{eqnarray*} \]

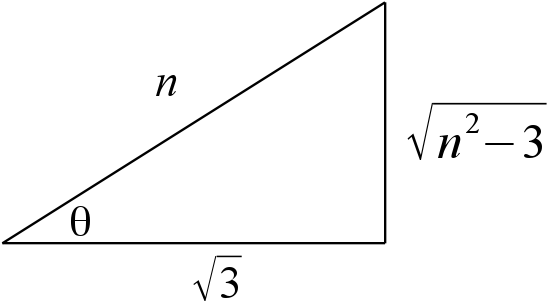
a solução dessa equação requer utilizar as seguentes substituições: \[ \begin{eqnarray*} n =& t+2\\ dn =& dt \end{eqnarray*} \] vamos solucionar a integral indefinida, assim a integral muda para \[ \begin{eqnarray*} I =& \int \sqrt{n^2 - 3} dn\\ \end{eqnarray*} \] utilizando substituição trigonométrica, vemos que colocando $u$ na hipotenusa e $\sqrt{3}$ no cateto adjacente, então \[ \begin{eqnarray*} \sqrt{n^2 - 3} =& \sqrt{3}\tan \theta\\ \dfrac{n}{\sqrt{3}} =&\sec \theta\\ dn =& \sqrt{3} \sec \theta \tan \theta d\theta \end{eqnarray*} \] de onde \[ \begin{array}{r l} I =& 3\int \sec \theta \tan ^2 \theta d\theta \nonumber\\ =& 3\int \sec \theta \left( \sec ^2 \theta - 1\right)d\theta \nonumber\\ =& 3\int \sec ^3 \theta d\theta - 3\int \sec \theta d\theta \nonumber \end{array} \] resolvendo cada uma das integrais: \[ \begin{array}{r l} I_2 = \int \sec \theta d\theta =&\int \sec \theta \dfrac{\sec \theta + \tan \theta}{\sec \theta + \tan \theta} d\theta \nonumber\\ =& \dfrac{\sec ^2 \theta + \sec \theta \tan \theta}{\sec \theta + \tan \theta} d\theta \nonumber \end{array} \] fazemos \[ \begin{array}{r l} u =& \sec \theta + \tan \theta \nonumber\\ du =& \left( \sec \theta \tan \theta + \sec^2 \theta\right) d\theta \nonumber \end{array} \] assim \[ \begin{array}{r l} I_2^* =& \int \dfrac{1}{u}\,du\nonumber\\ I_2=& \ln \left| \sec \theta + \tan \theta \right| + C_1\nonumber \end{array} \] A I integral: \[ \begin{array}{r l} I_1 =& \sec ^3 \theta d\theta\nonumber\\ \end{array} \] integrando por partes: \[ \begin{array}{r l c r l} u =& \sec \theta &\;\;\;\;\ & dv =& \sec ^2 \theta d\theta\nonumber\\ du =& \sec \theta \tan \theta d\theta & & v =& \tan \theta \nonumber \end{array} \] assim \[ \begin{array}{r l} \sec ^3 \theta d\theta =& \sec \theta \tan \theta - \int \left( \sec ^3 \theta - \sec \theta \right)d\theta \nonumber\\ 2\sec ^3 \theta d\theta =& \sec \theta \tan \theta - \int \sec \theta d\theta \nonumber\\ \sec ^3 \theta d\theta =& \dfrac{1}{2}\sec \theta \tan \theta - \dfrac{1}{2} \ln \left| \sec \theta + \tan \theta \right| + C_2\nonumber \nonumber \end{array} \] assim a integral original fica \[ I = \dfrac{1}{2}\sec \theta \tan \theta + \dfrac{1}{2} \ln \left| \sec \theta + \tan \theta \right| + C\nonumber \] como \[ \sec \theta = \dfrac{t+2}{\sqrt{3}}\;\;\;\;\;\; \tan \theta = \dfrac{\sqrt{(t+2)^2 -3}}{\sqrt{3}}\nonumber \] então \[ \int \sqrt{(t+2)^2 -3}\,\,dt = \dfrac{\left(t+2 \right)\sqrt{(t+2)^2 -3}}{2} - \frac{3}{2}\ln \left| \dfrac{t+2+\sqrt{(t+2)^2 -3}}{\sqrt{3}} \;\;\;\right|\nonumber \]

Exemplo 04

Encontre o comprimento do arco de uma hélice depois de completar uma volta inteira, sabendo que a parametrização da curva está dada por $\mathbf{r}(t) = a\cos t \,\mathbf{i} + a \sin t \,\mathbf{j} + \sqrt{1-a^2} t \,\mathbf{k}$
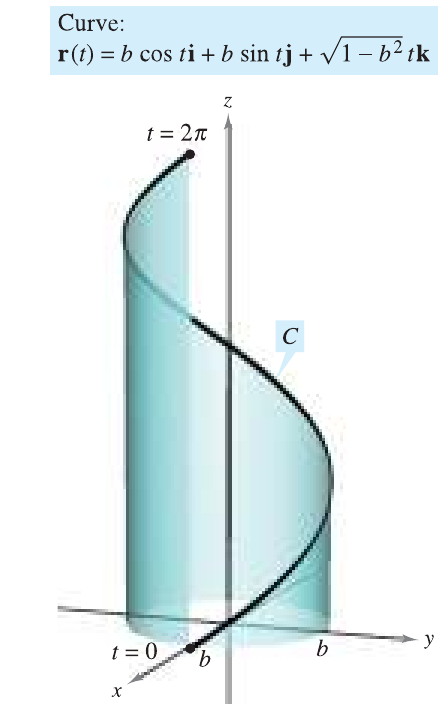
SOL.
Derivando a expressão \[ \mathbf{r}'(t) = -a\sin t \,\mathbf{i} + a \cos t \,\mathbf{j} + \sqrt{1-a^2} \,\mathbf{k} \nonumber \] uma volta inteira quer dizer que a integral é de $0$ até $2\pi$, assim: \[ \begin{eqnarray*} L &=& \int_0^{2\pi} \sqrt{a^2\sin ^2t + a^2\cos ^2t + (1-a^2)}\,\,\;\;\;dt\\ &=& \int_0^{2\pi} dt\\ &=& \left. t\right|_0^{2\pi}\\ &=& 2\pi \end{eqnarray*} \]

Exemplo 05

Para a hélice $\mathbf{r}(t) = a\cos t\,\mathbf{i} + a\sin t \,\mathbf{j} + bt\,\mathbf{k}$, selecionar $P_o = a\,\mathbf{i}$
SOL.
Nota que quando $\mathbf{r}(t) = a\,\mathbf{i} = a\cos t\,\mathbf{i} + a\sin t \,\mathbf{j} + bt\,\mathbf{k}$ então necessariamente $t=0$, assim o limite inferior de integração é $0$: \[ \begin{eqnarray*} L(t) &=& \int_0^t \sqrt{a^2\sin ^2t + a^2\cos ^2t + b^2}\;\;\;d\tau\\ &=& \int_0^t \sqrt{a^2 + b^2}\;\;\;d\tau\\ &=& \sqrt{a^2 + b^2}\;\;t \end{eqnarray*} \] agora diremos que esse resultado corresponde à variável $l$ e invertemos \[ \begin{eqnarray*} l &=& \sqrt{a^2 + b^2}\;\;t\\ t &=& \dfrac{l}{\sqrt{a^2 + b^2}} \end{eqnarray*} \] agora substituímos o $t$ na equação original \[ \mathbf{r}(t) = a\cos\left(\dfrac{l}{\sqrt{a^2 + b^2}} \right) \,\mathbf{i} + a\sin\left(\dfrac{l}{\sqrt{a^2 + b^2}} \right) \,\mathbf{j} + \dfrac{bl}{\sqrt{a^2 + b^2}}\,\mathbf{k} \nonumber \]

Exemplo 06

Dada uma curva $C$ representada por $\left| \mathbf{r}(t) \right|=1$, então o parâmetro $t$ é o parâmetro comprimento de arco de $C$
SOL.
Por definição de comprimento de arco: \[ \begin{eqnarray*} l = L(t) &=& \int_0^t\left| \mathbf{r}(\tau) \right|\;\;\;d\tau\\ &=& \int_0^t1\;d\tau\\ &=& t \end{eqnarray*} \nonumber \] Deste exemplo vemos que parametrizando a curva com o arco de comprimento estamos escolhendo um parametrização tal que o módulo da função vetorial é nulo. Podemos ainda ir a frente um pouco mais nesta análise, como \[ \begin{eqnarray} l = L(t) &=& \int_a^t \left| \dfrac{d\mathbf{r}(t)}{dt} \right|\;\; dt\nonumber\\ \dfrac{dl}{dt} &=& \left| \dfrac{d\mathbf{r}(t)}{dt} \right|\label{def25} \end{eqnarray} \] vamos aplicar a regra da cadeia: \[ \dfrac{d\mathbf{r}(t)}{dt} = \dfrac{d\mathbf{r}(l)}{dl}\dfrac{dl}{dt} \nonumber \] do $\ref{def35}$, podemos escrever: \[ \dfrac{d\mathbf{r}(t)}{dt} = \dfrac{d\mathbf{r}(l)}{dl}\left|\, \dfrac{d\mathbf{r}(t)}{dt} \right| \] ou, equivalentemente \[ \dfrac{d\mathbf{r}(l)}{dl} = \mathbf{r}'(l) = \dfrac{\mathbf{r}'(t)}{\left| \dfrac{d\mathbf{r}(t)}{dt} \right|} \nonumber \] ou, mais claramente \[ \mathbf{r}'(l) = \dfrac{\mathbf{r}'(t)}{\left|\mathbf{r}'(t)\right|} \nonumber \] o que significa que a curva parametrizada é um curva vectorial com módulo unitário, como visto no exemplo, mas é aquela cuja taxa de variação em relação a $t$ é um, isto é dito por alguns autores como a rapidez da curva é $1$.

Exemplo 07

Calcule a curva parametrizada em $l$ da função vetorial $\mathbf{r}(t) = t \,\mathbf{i} + \dfrac{\sqrt{2}}{2}t^2\,\mathbf{j} + \dfrac{1}{3}t^3\,\mathbf{k}$
SOL.
A derivada da função é $\mathbf{r}(t) = \,\mathbf{i} + \sqrt{2t}\,\mathbf{j} + t^2\,\mathbf{k}$ \[ \begin{eqnarray*} l(t) &=& \int_0^t \sqrt{1+2\tau+\tau^4}\;\;d\tau\\ &=& \int_0^t \sqrt{\left( 1+\tau^2\right)^2}\;\;d\tau\\ &=& \int_0^t \left( 1+\tau^2\right)\;\;d\tau\\ &=& \int_0^t t + \dfrac{1}{3}t^3 \end{eqnarray*} \]

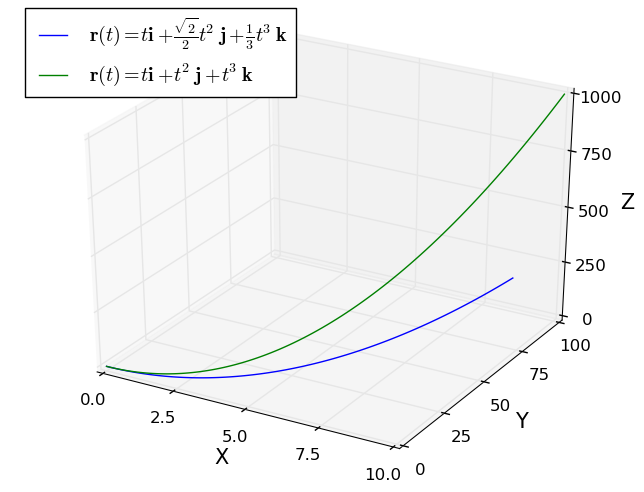
A parametrização das curvas é um assunto delicado, por exemplo observe a figura do lado, nessa figura plotamos a curva anterior e uma outra curva, dada por $\mathbf{r}(t) = t\,\mathbf{i} + t^2\,\mathbf{j} + t^3\,\mathbf{k}$, que é essencialmente a mesma curva, são suaves e tem o mesmo comportamento porém quando você tenta calcular a parametrização utilizando o comprimento do arco resulta em um desastre: \[ \mathbf{r}'(t) = \,\mathbf{i} + 2t\,\mathbf{j} + 3*t^2\,\mathbf{k} \nonumber \] de onde \[ l(t) = \int_0^t \sqrt{1 + 4\tau^2 + 9\tau ^4}\;\;d\tau \nonumber \] vemos que essa integral não é simples de ser resolvida.