Exemplo 01
Um tanque $T$ tem forma de um cilindro circular reto de raio $1\,m$ e altura de $3\,m$. O tanque está cheio de uma substancia líquida. Cada partícula dessa substância está sujeita a uma pressão que é proporcional à distância da partícula até a superfície livre do líquido. Usando coordenadas cartesianas, definir uma função escalar que descreva o campo de pressão no interior de $T$.
SOL.
A posição de qualquer ponto do tanque está dada pela terna $(x,y,z)$. Segundo o problema a pressão sobre uma partícula é proporcional à distância até a superfície, como o tanque tem $3\,m$ então $P=P_0\left( 3 - z \right)$
Exemplo 02
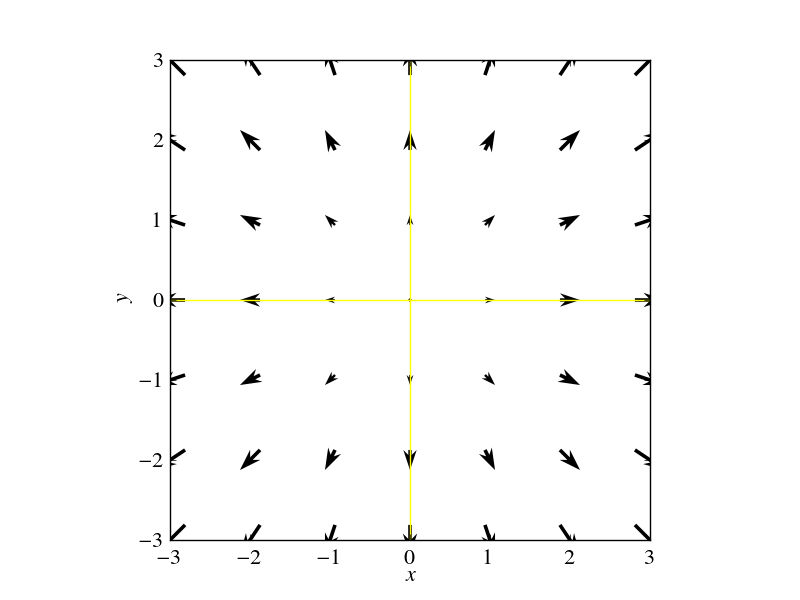
Dada a função $\mathbf{r}(x,y) = x \,\mathbf{i} + y \,\mathbf{j}$, desenhe o campo resultante.
SOL.
Exemplo 03
Seja $f(x,y) = xe^y$ $P=(2,-1)$ e $\mathbf{u}=< 2,3 >$, calcule a derivada direcional de $f$ ao longo de $\mathbf{u}$ avaliada no ponto $P$.
SOL.
Primeiro devemos calcular o vetor unitário de $\mathbf{u}$. Por definição
\[
\begin{align*}
\mathbf{\hat{u}} =& \dfrac{\mathbf{u}}{\left| \mathbf{u} \right|}\\
=& \dfrac{2\,\mathbf{i} + 3 \,\mathbf{j}}{\sqrt{4 + 9}}\\
=& \dfrac{2}{\sqrt{13}}\,\mathbf{i} + \dfrac{3}{\sqrt{13}}\,\mathbf{j}
\end{align*}
\]
Da definição da derivada direcional
\[
\begin{align*}
D_{\mathbf{u}} =& \lim _{h\rightarrow 0}\dfrac {f\left( x_{0}+ha,\,y_{0}+hb\right) -f\left( x_{0},\,y_{0}\right) } {h}\\
=& \lim _{h\rightarrow 0}\dfrac {f\left( 2 +h\dfrac{2}{\sqrt{13}},\, -1+h\dfrac{3}{\sqrt{13}} \right) -f\left(2,\, -1 \right) } {h}\\
=& \lim _{h\rightarrow 0} \dfrac { \left( 2 +\dfrac{2h}{\sqrt{13}} \right)\,e^{\dfrac{3h}{\sqrt{13}}-1} - \left(2 \right)\, e^{-1} } {h}\\
=& \lim _{h\rightarrow 0} \dfrac { 2\,e^{\dfrac{3h}{\sqrt{13}}-1} + \dfrac{2h}{\sqrt{13}} \,e^{\dfrac{3h}{\sqrt{13}}-1} - 2e^{-1}} {h}\\
=& 2e^{-1}\lim _{h\rightarrow 0} \dfrac { e^{\dfrac{3h}{\sqrt{13}}} - 1} {h} + e^{-1}\lim _{h\rightarrow 0} \dfrac { \dfrac{2\bcancel{h}}{\sqrt{13}} \,e^{\dfrac{3h}{\sqrt{13}}}} {\bcancel{h}}\\
=& \dfrac{6e^{-1}}{\sqrt{13}}\lim _{h\rightarrow 0} e^{\dfrac{3h}{\sqrt{13}}} + \dfrac{2e^{-1}}{\sqrt{13}}\lim _{h\rightarrow 0} e^{\dfrac{3h}{\sqrt{13}}}\\
=& \dfrac{8e^{-1}}{\sqrt{13}}
\end{align*}
\]
Exemplo 04
\[
f(x,y) = \dfrac{x^2}{10} - \dfrac{y^2}{9}
\nonumber
\]
(a) Determine o gradiente de $f$ em $R = (4,3)$. Utilize o gradiente para calcular a derivada direcional de $R$ na direção de $R$ para $Q=(5,6)$
SOL.
a)
\[
\begin{align*}
\mathbf{\nabla} f =& f_x \,\mathbf{i} + f_y \,\mathbf{j}\\
=& \dfrac{x}{8}\,\mathbf{i} + \dfrac{2y}{9}\,\mathbf{j}
\end{align*}
\]
b)
\[
\begin{align*}
\mathbf{v} =& (5-4) \,\mathbf{i} + (6-3)\,\mathbf{j}\\
=& \,\mathbf{i} + 3\,\mathbf{j}
&\\
\hat{v} = & \dfrac{\mathbf{v}}{|\mathbf{v}|}\\
=& \dfrac{\,\mathbf{i} + 3\,\mathbf{j}}{\sqrt{10}}\\
&\\
D_{\mathbf{u}}f(x,y) =& \left( \dfrac{1}{\sqrt{10}}\,\mathbf{i} + \dfrac{3}{\sqrt{10}}\,\mathbf{j} \right)\cdot \left( \dfrac{x}{8}\,\mathbf{i} + \dfrac{2y}{9}\,\mathbf{j} \right)\\
=& \dfrac{x}{8\sqrt{10}} + \dfrac{2y}{3\sqrt{10}}\\
D_{\mathbf{u}}f(4,3) =& \dfrac{1}{2\sqrt{10}} + \dfrac{2}{\sqrt{10}}\\
\approx & 0.79
\end{align*}
\]
Exemplo 05
A temperatura na superfície de um metal está dada por (em graus Celsius);
\[
f(x,y) = 20 - 4x^2 - y^2
\nonumber
\]
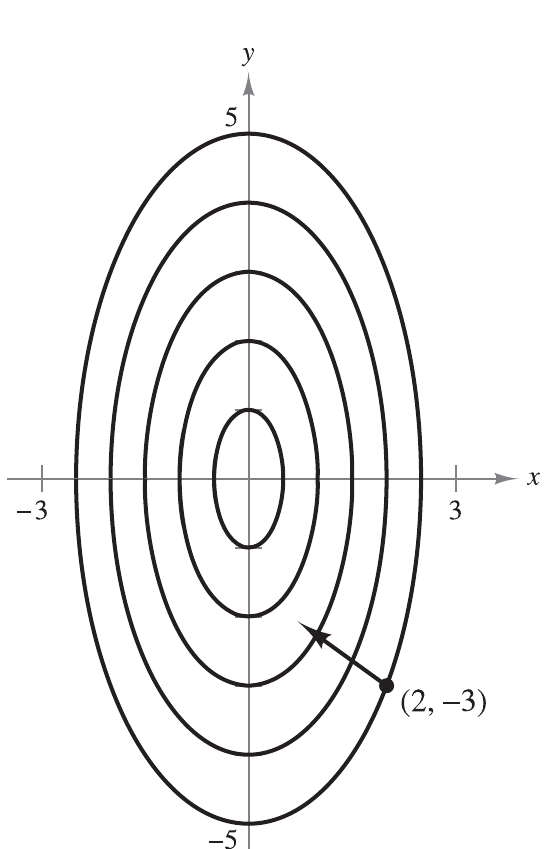
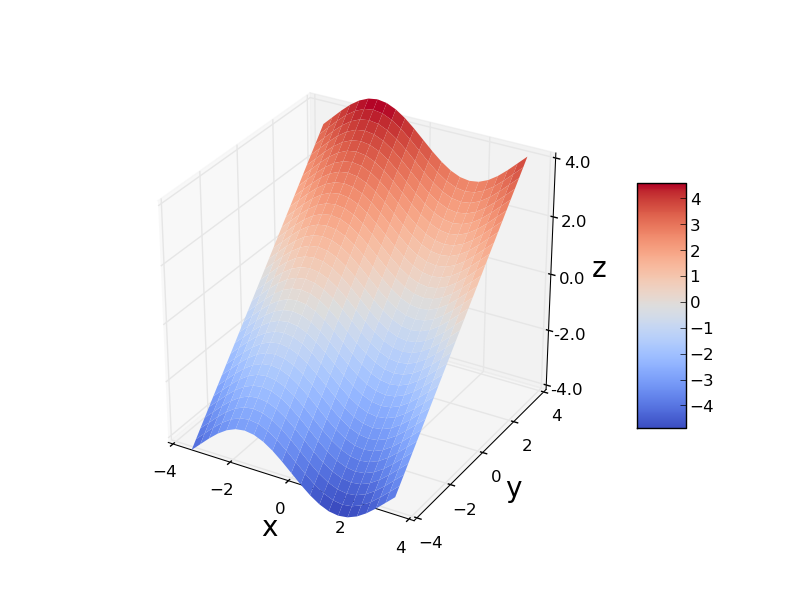
onde $x$ e $y$ estão medidos em centímetros. Em que direção no ponto $(2,-3)$ a temperatura aumenta mais rapidamente. Qual é a taxa de incremento?
SOL.
\[
\begin{align*}
\mathbf{\nabla}\,T(x,y) =& T_x(x,y) \,\mathbf{i} +T_y(x,y) \,\mathbf{j}\\
=& -8 x\,\mathbf{i} - 2y \,\mathbf{j}\\
\end{align*}
\]
assim, a direção de máximo incremento a partir do ponto $(2,-3)$ é
\[
\mathbf{\nabla}\,T(2,-3) = -16\,\mathbf{i} +6 \,\mathbf{j}
\nonumber
\]
esse vetor é mostrado na figura embaixo, a esquerda a figura da superfície e à direita as curvas de nível. A taxa de máximo incremento está dada por
\[
\left|\mathbf{\nabla}\,T(2,-3) \right| = \sqrt{256 + 36} = \sqrt{292} \approx 17,09^\circ\mbox{ por centímetros}
\nonumber
\]
Exemplo 06
Uma partícula está localizada no ponto $(2,-3)$ sobre uma superfície metálica aquecida à temperatura dada por
\[
T(x,y) = 20 - 4x^2 - y^2
\nonumber
\]
Encontre o caminho que a partícula deve seguir a fim de atingir o ponto mais quente da superfície.
SOL.
A posição da partícula em qualquer instante está dada pelo vetor
\[
\mathbf{r}(t) = x(T)\,\mathbf{i} + y(t) \,\mathbf{j}
\nonumber
\]
Fisicamente sabemos que a direção do movimento está determinada pela direção da velocidade (em última instancia, é claro) a qual está dada por
\[
\mathbf{r}'(t) = \dfrac{x}{dt}\,\mathbf{i} + \dfrac{y}{dt} \,\mathbf{j}
\nonumber
\]
a partícula atingirá seu objetivo no instante em que a velocidade apontar para o ponto mais quente na superfície o qual estará dado pelo gradiente da função
\[
\mathbf{\nabla}\,T(x,y) = -8 x\,\mathbf{i} - 2y \,\mathbf{j}
\nonumber
\]
assim basta igualar ambos vetores, com a ressalva de que para poder acoplarlos colocaremos uma constante de proporcionalidade entre eles, a qual pode ser função do tempo:
\[
-8 x\,\mathbf{i} - 2y \,\mathbf{j} = k \left( \dfrac{x}{dt}\,\mathbf{i} + \dfrac{y}{dt} \,\mathbf{j} \right)
\nonumber
\]
de onde
\[
\begin{align*}
-8x =& k\dfrac{x}{dt}\\
2y =& k\dfrac{y}{dt}
\end{align*}
\]
dessas duas equações escrevemos
\[
\dfrac{dx}{-4x} = \dfrac{dy}{y}
\nonumber
\]
integrando obtemos
\[
x = \dfrac{1}{81} y^4
\nonumber
\]
Exemplo 07
Esboce a curva de nível para $c=0$ da função dada por \[ f(x,y) = y - \sin x \nonumber \] e encontre os vetores normais em vários pontos da curva
SOL.
A curva em $c=0$ está dada por \[ \begin{align*} 0 =& y - \sin x\\ y =& \sin x \end{align*} \] Como mostra a figura à esquerda. O gradiente de $f$ em $(x,y)$ está dado por \[ \begin{align*} \mathbf{\nabla} f(x,y) =& f_x(x,y)\,\mathbf{i} + f_y(x,y) \,\mathbf{j}\\ =& -\cos x\,\mathbf{i} + \,\mathbf{j} \end{align*} \] do teorema anterior sabemos que $\mathbf{\nabla} f(x,y)$ é normal à curva em quamquer ponto $(x,y)$. Alguns valores do gradiente são: \[ \begin{align*} \mathbf{\nabla} f\left(-\pi,0\right) =& \,\mathbf{i} + \,\mathbf{j}\\ \mathbf{\nabla} f\left(-\dfrac{2\pi}{3},-\dfrac{\sqrt{3}}{2}\right) =& -\dfrac{1}{2}\,\mathbf{i} + \,\mathbf{j}\\ \mathbf{\nabla} f\left(-\dfrac{\pi}{2},-1\right) =& \,\mathbf{j}\\ \mathbf{\nabla} f\left(-\dfrac{\pi}{3},\dfrac{\sqrt{3}}{2}\right) =& -\dfrac{1}{2}\,\mathbf{i} + \,\mathbf{j}\\ \mathbf{\nabla} f\left(0,0\right) =& -\,\mathbf{i} + \,\mathbf{j}\\ \mathbf{\nabla} f\left(-\dfrac{\pi}{3},\dfrac{\sqrt{3}}{2}\right) =& \,-\dfrac{1}{2}\mathbf{i} + \,\mathbf{j}\\ \mathbf{\nabla} f\left(\dfrac{\pi}{2},1\right) =& \,\mathbf{j} \end{align*} \]
Exemplo 08
Encontrar a equação da reta tangente à curva $x^2+y^2=4$ no ponto $\left( \sqrt{3}, 1 \right)$, utilizando o gradiente.
SOL.
\[
\begin{align*}
\mathbf{\nabla}f =& 2x\,\mathbf{i} + 2y\,\mathbf{j} \\
\mathbf{\nabla}f(x_0,y_0) \cdot \left( \mathbf{r} - \mathbf{r_0}\right) =&0\\
\left[2(\sqrt{3}) \,\mathbf{i} - 2(1)\,\mathbf{j}\right] \cdot \left[\left( x - \sqrt{3}\right)\,\mathbf{i} + \left(y - 1\right)\,\mathbf{j} \right]=& 0\\
\left( 2\sqrt{3}x - 6\right) + 2y - 2 =& 0\\
\end{align*}
\]
de onde
\[
y = 4 - \sqrt{3}x
\nonumber
\]
Exemplo 09
Considere a superfície $D$ definida pela equação $x^3y-yz+z^5=9$. Calcular o plano tangente a $S$ no ponto $(3,-1,2)$
SOL.
Vamos utilizar a equação $\mathbf{\nabla}\,f(P_0)\cdot\left( \mathbf{r} - \mathbf{r_0} \right) = \mathbf{0}$. Para isso identificamos que o ponto $P_0$ que é determinado pelo vetor $r_0$ está dado por $\mathbf{r}_0 = 3\,\mathbf{i} - \,\mathbf{j} +2 \,\mathbf{k}$. Agora calculamos o gradiente
\[
\begin{align*}
\mathbf{\nabla}\,f(3,-1,2) =& \left. 3x^{2}y\,\mathbf{i} +\left( x^{3}-z^{2}\right)\,\mathbf{j} +\left( 5z^{4}-2yz\right)\mathbf{k} \right|_{\;\;\;\;(3,-1,2)}\\
=& -27\,\mathbf{i} +23 \,\mathbf{j} +84 \,\mathbf{k}
\end{align*}
\]
da mesma forma
\[
\mathbf{r} - \mathbf{r_0} = \left( x-3\right)\,\mathbf{i} +\left( y+1\right)\,\mathbf{j} +\left( z-2\right) \,\mathbf{k}
\nonumber
\]
por tanto
\[
\mathbf{\nabla}\,f(P_0)\cdot\left( \mathbf{r} - \mathbf{r_0} \right) = -27\left( x-3\right) + 23 \left( y+1\right) + 84 \left( z-2\right) = 0
\nonumber
\]
ou equivalentemente
\[
-27x+23y=84z=64
\nonumber
\]
Exemplo 09
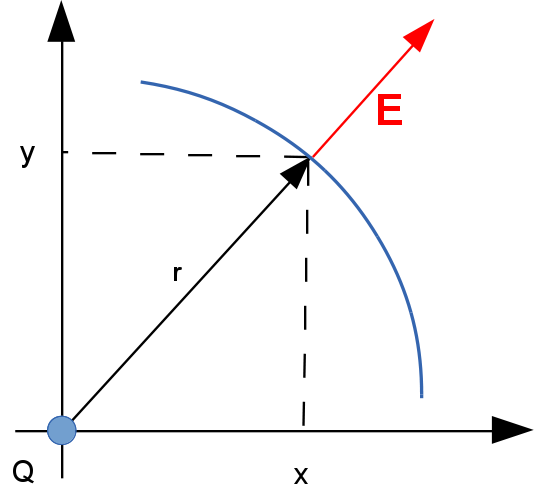
Considere uma carga elétrica positiva $Q$, situada na origem de um plano $xy$, conforme a figura conforme a figura. Sabendo que as curvas equipotenciais são descritas por circunferências em torno da carga e tem valor dado por \[ V = \dfrac{Q}{r}, \nonumber \] calcule o campo vetorial, $\mathbf{E}$, associado ao campo escalar.
SOL.
O potencial medido sobre qualquer ponto de uma das linhas equipotenciais está dado por
\[
\begin{align*}
V =& \dfrac{Q}{r}\\
=& \dfrac{Q}{\sqrt{x^2 + y^2}}
\end{align*}
\]
como o campo deriva do potencial, então podemos escrever
\[
\begin{align*}
\mathbf{E} =& \mathbf{\nabla} V(x,y)\\
=& V_x(x,y) \,\mathbf{i} + V_y(x,y) \,\mathbf{j}\\
=& \dfrac{\partial \;}{\partial x} \left( \dfrac{Q}{\sqrt{x^2 + y^2}} \right) \,\mathbf{i} + \dfrac{\partial \;}{\partial y} \left( \dfrac{Q}{\sqrt{x^2 + y^2}} \right) \,\mathbf{j}\\
=& \dfrac{Q}{\left(x^2 + y^2\right)^{3/2}} x\,\mathbf{i} +
\dfrac{Q}{\left(x^2 + y^2\right)^{3/2}} y\,\mathbf{j}\\
=& \dfrac{Q}{\left(x^2 + y^2\right)} \dfrac{x\,\mathbf{i} + y\,\mathbf{j}}{\sqrt{x^2 + y^2}}\\
=& \dfrac{Q}{r^2} \mathbf{\hat{r}}
\end{align*}
\]