Divergência
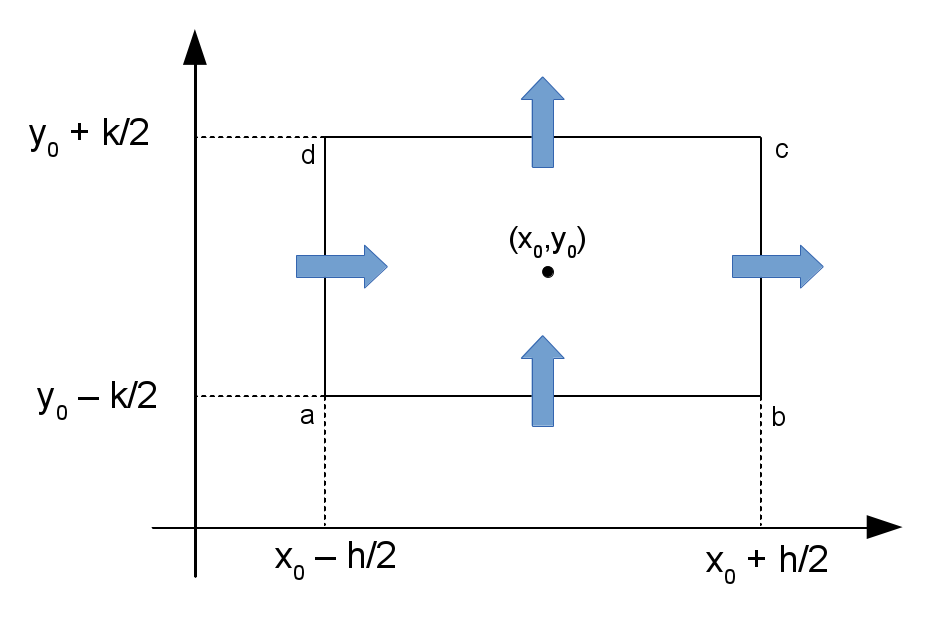
Vamos supor que $\mathbf{V}:U\subseteq \mathbb{R}^2 \to \mathbb{R}^2$, $\mathbf{V}= V_x\,\mathbf{i} + V_y \,\mathbf{j}$ é o campo de velocidades de uma corrente de um fluído. Queremos estimar quanta massa por unidade de tempo está saindo de uma "pequena" região de $U$. Seja $\mathbf{p}=(x_0,\,y_0)\in U$ e considere o retângulo $R$ com centro em $\mathbf{p}$ dado por \[ R=\left\{ \left( x,y\right) |x_{0}-\dfrac{h}{2}\leq x\leq x_{0}+\dfrac{h}{2},\,y_{0}-\dfrac{k}{2}\leq y\leq y_{0}+\dfrac{k}{2} \right\} \nonumber \] Escolhendo $h$ e $k$ suficientemente pequenos teremos garantia de que $R\subset U$.
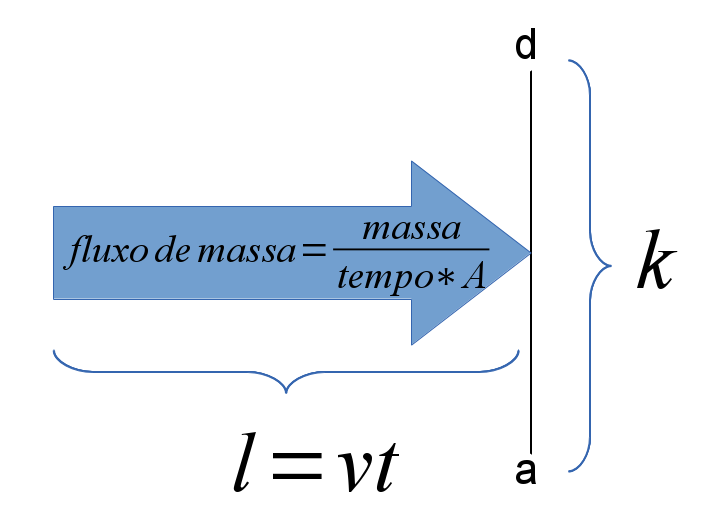
Suponhamos que o segmento $ad$ representa um dos lado do retângulo $R$, a massa que atravessa esse segmente está dada por $m=\sigma lk$, ($\sigma$ é a densidade de massa superficial) como $l=\left|\mathbf{V}\right|t$ então a massa por unidade de tempo que atravessa será \[ \dfrac{m}{t}=\sigma \;k\; \left|\mathbf{V}\right| \nonumber \] de onde vemos que essa grandeza é diretamente proporcional ao produto do módulo da velocidade e o comprimento do segmento a ser atravessado.
Da figura é obvio que a componente $V_x$ de $\mathbf{V}$ atravessará os lados $ad$, $bc$ de $R$ enquanto que a componente $V_y$ atravessará os lados $cd$ e $ab$. Consideraremos como sendo negativo o fluído que entra pelos lados $ab$ e $bc$ e positivo o fluído que sai pelos lados $cd$ $bc$. As seguintes expressões dão conta do fluído que atravessa o perímetro do retângulo $R$ \[ \begin{align*} \dfrac{m}{t}\text{ que entra por }ab \approx & h\,V_y(x_0,y_0-k/2)\\ \dfrac{m}{t}\text{ que entra por }ad \approx & k\,V_x(x_0-h/2,y_0)\\ \dfrac{m}{t}\text{ que sai por }cd \approx & h\,V_y(x_0,y_0+k/2)\\ \dfrac{m}{t}\text{ que sai por }bc \approx & k\,V_x(x_0+h/2,y_0) \end{align*} \] Note que $h$ é o comprimento do retângulo entre $ab$ e $bc$ e $2k$ é o comprimento do retângulo entre $cd$ $bc$. A expressão $V_y(x_0,y_0-k/2)$ significa o valor de $V_y$ no ponto $(x_0,y_0-k/2)$.
Assim a quantidade de fluído que sai do retângulo é \[ \begin{align*} \text{Total $m/t$ que sai de }R =& (bc - ad) + (cd - ab)\\ =& k\left[ V_x(x_0+h/2,y_0) - V_x(x_0-h/2,y_0)\right] + h\left[ V_y(x_0,y_0+k/2) - V_y(x_0,y_0-k/2) \right] \end{align*} \] dividindo pela área do retângulo $A=hk$: \[ \dfrac{\text{Total $m/t$ que sai de }R}{\text{área}} = \dfrac{V_x(x_0+h/2,y_0) - V_x(x_0-h/2,y_0)}{h} - \dfrac{V_y(x_0,y_0+k/2) - V_y(x_0,y_0-k/2)}{k} \nonumber \] Como queremos saber quanta massa sai do ponto $P=(x_0,\,y_0)$ faremos com que $k\to 0$ e $h \to 0$, isto é \[ \begin{align*} \lim_{\,\text{área}\to 0} \dfrac{\text{Total que sai de }R}{\text{área}}=& \lim_{h\to 0}\dfrac{V_x(x_0+h/2,y_0) - V_x(x_0-h/2,y_0)}{h} + \lim_{k\to 0} \dfrac{V_y(x_0,y_0+k/2) - V_y(x_0,y_0-k/2)}{k}\\ =& \dfrac{\partial V_x}{\partial x} + \dfrac{\partial V_y}{\partial y}\\ =& \left( \dfrac{\partial \;}{\partial x}\,\mathbf{i} + \dfrac{\partial \;}{\partial y}\,\mathbf{j} \right) \cdot \left( V_x\,\mathbf{i} + V_y \,\mathbf{j} \right)\\ =& \mathbf{\nabla}\cdot \mathbf{V} \end{align*} \] O resultado obtido define uma nova grandeza e uma nova operação: a densidade de corrente e a divergência do campo $\mathbf{V}$. A densidade de corrente de massa, $\mathbf{j}$, é a quantidade de massa que sai de uma região do espaço por unidade de tempo e por unidade de área. A divergência e definida pelo produto $\mathbf{\nabla}\cdot \mathbf{V}$. A continuação definimos formalmente o conceito de divergência
| Definição |
|
Seja $\mathbf{F}:U\subseteq \mathbb{R}^3 \to \mathbb{R}^3$ um campo vetorial diferenciável. A divergência de $\mathbf{F}$, denotada por $div\,\mathbf{F}$ ou $\mathbf{\nabla}\cdot \mathbf{F}$ é o campo escalar definido por \[ div\,\mathbf{F}=\mathbf{\nabla}\cdot \mathbf{F}= \dfrac{\partial F_x}{\partial x} + \dfrac{\partial F_y}{\partial y} + \dfrac{\partial Fz}{\partial z} \nonumber \] onde $F_x, \, F_y\, F_z$ são as componente cartesianas de $\mathbf{F}$. |
Junto com o conceito de densidade de corrente podemos entender o porque do nome divergência, em termos de um fenômeno físico podemos dizer que se $\mathbf{F}$ é o campo de velocidades de um gás em expansão, então a divergência em um ponto $P$ é á velocidade com a qual esse gás está se expandindo (divergindo) no ponto $P$. Dessa forma vemos que se \[ \begin{align*} \mathbf{\nabla}\cdot \mathbf{F} > 0 \Rightarrow & \text{fluído em expansão}\\ \mathbf{\nabla}\cdot \mathbf{F} < 0 \Rightarrow & \text{fluído em compressão}\\ \mathbf{\nabla}\cdot \mathbf{F} = 0 \Rightarrow & \text{fluído incompressível}\\ \end{align*} \]
Exemplo 10
Se $\mathbf{F}= x^2y\,\mathbf{i} + xz \,\mathbf{j} +xyz \,\mathbf{k}$, calcule a divergência do campo.
SOL.
\[
\begin{align*}
\mathbf{\nabla}\cdot \mathbf{F} =& \dfrac{\partial x^2y}{\partial x} + \dfrac{\partial xz}{\partial y} + \dfrac{\partial xyz}{\partial z}\\
=& 2xy +xy\\
=& 3xy
\end{align*}
\]
| Propriedades da divergência |
|
Sejam
\[\mathbf{f}(x,y,z) = f_1(x,y,z) \,\mathbf{i} +f_2(x,y,z) \,\mathbf{j} + f_3(x,y,z) \,\mathbf{k}\;\; e\\
\mathbf{g}(x,y,z) = g_1(x,y,z) \,\mathbf{i} +g_2(x,y,z) \,\mathbf{j} + g_3(x,y,z) \,\mathbf{k}
\nonumber
\]
funções vetoriais definidas num domínio $D$. Suponhamos também que $div\,f$ e $div\,g$ existem, então:
|
Equação de continuidade
Uma aplicação da divergência é em mecânica dos fluídos onde temos a equação de continuidade de matéria \[ \nabla \cdot \mathbf{u} + \dfrac{\partial \rho}{\partial t} = 0 \nonumber \] onde $u=\rho \mathbf{v}$, sendo $\rho=\rho(x,y,z,t)$ a densidade do fluído e $\mathbf{v}= \mathbf{v}(x,y,z,t)$ o vetor velocidade.
Note que se rescrevemos a equação como \[ \dfrac{\partial \rho}{\partial t} = -\nabla \cdot \mathbf{u} \nonumber \] fica evidente que a divergência é uma medida da variação da densidade do fluído num ponto. Assim quando a divergência é positiva, a densidade no ponto está diminuindo com o tempo, e por isso que dizemos que nesse ponto o fluído está se expandindo. Obviamente que também fica claro que os fluídos onde $\rho\neq\rho(t)$ serão chamados de incompressíveis. Os campos que verifiquem $\vec{\nabla}\cdot \mathbf{F}=0$ são chamados de campos solenoidais pois O campo se comporta como o campo magnético gerado por um solenoide (bobina).
Equação de Laplace
Até este momento definimos duas novas operações, o gradiente que transforma um campo escalar em um campo vetorial e a divergência que transforma um campo vetorial em um campo escalar. O passo a seguir é misturar ambas operações tomaremos um campo escalar e transformaremos em um campo vetorial e a seguir esse campo será transformado em outro campo escalar.
| Equação de Laplace |
|
Seja $f$ um campo escalar definido num conjunto aberto definido em $\mathbb{R}^3$, a equação de Laplace é a equação definida pela divergência do gradiente do campo escalar, isto é \[ \nabla^2 f= \mathbf{\nabla} \cdot \left( \mathbf{\nabla} f\right) = 0 \nonumber \] onde o operador diferencial atuando sobre o campo $\displaystyle \nabla^2$ é conhecido como operador laplaciano e está definido como \[ \nabla^2 = \dfrac{\partial^2 \;}{\partial x^2} + \dfrac{\partial^2 \;}{\partial y^2} + \dfrac{\partial^2 \;}{\partial z^2} \nonumber \] |
A equação de Laplace é um caso especial da equação de Poisson \[ \nabla^2 f= g \nonumber \] onde $g$ também é uma função escalar.
Para entender o significado do Laplaciano é bom analisar o significado do operador em uma dimensão $\displaystyle \dfrac{\partial^2 f}{\partial x^2}$. Sabemos do cálculo I que se a II derivada da função é positiva, então $f(x)$ deve ser côncava, caso contrario a função é convexa. Assim $\nabla^2 f(x_0,y_0)$ será positiva se ela o valor de $ f(x_0,y_0)$ for menor na média que o valor de $f(x,x)$ em torno do ponto $P=(x_0,y_0)$. Por exemplo uma das equação onde este operador aparece é a equação de condução do calor a qual estipula que \[ \nabla^2 T = \dfrac{c}{\kappa}\dfrac{\partial T}{\partial t} \nonumber \] onde $T$ é a temperatura, $c$ é o calor específico e $\kappa$ é a condutividade térmica. Note que $\nabla^2 T$ é positiva então $T$ tem um valor localmente menor que os vizinho em média, por tanto $\dfrac{\partial T}{\partial t}>0$ o que significa que o ponto se devera esquentar. Se $\nabla^2 T$ é negativa então $T$ tem um valor localmente maior que os vizinho em média, por tanto $\dfrac{\partial T}{\partial t} < 0$ o que significa que o ponto se devera esfriar (calor fluirá desde o ponto).
É por isso que as funções que verificam a equação de Laplace são chamadas de funções harmônicas, pois na média os pontos não estão nem por cima nem por baixo.