Exemplos sobre rotacional

Exemplo 01

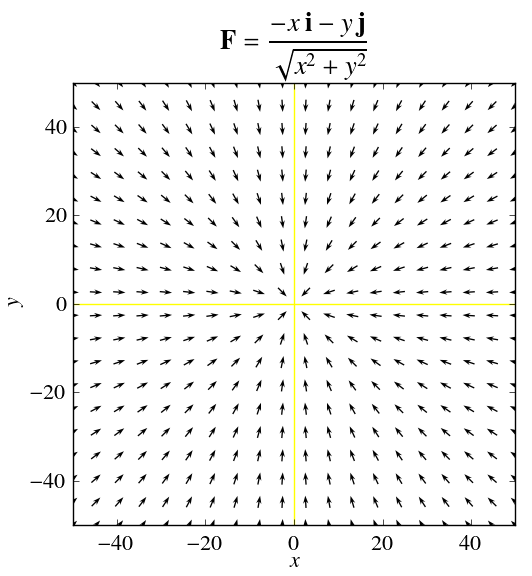
Calcule o campo rotacional de $\displaystyle \mathbf{F} = \dfrac{-x\,\mathbf{i} - y \,\mathbf{j}}{\sqrt{x^2+y^2}}$
SOL.

\[ \begin{align*} \vec{\nabla} \times \mathbf{F} =& \begin{bmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial \;}{\partial x} & \dfrac{\partial \;}{\partial y} & \dfrac{\partial \;}{\partial z}\\ \dfrac{-x}{\sqrt{x^2+y^2}} & \dfrac{-y}{\sqrt{x^2+y^2}} & 0 \end{bmatrix}\\ & \\ =&\left[ \dfrac{\partial \;}{\partial y} 0 - \dfrac{\partial \;}{\partial z} \left( \dfrac{-y}{\sqrt{x^2+y^2}} \right) \right]\;\mathbf{i} - \left[ \dfrac{\partial \;}{\partial x} 0 - \dfrac{\partial \;}{\partial z} \left( \dfrac{-x}{\sqrt{x^2+y^2}} \right) \right]\; \mathbf{j} +\\ & \left[ \dfrac{\partial \;}{\partial x} \left( \dfrac{-y}{\sqrt{x^2+y^2}} \right) - \dfrac{\partial \;}{\partial y} \left( \dfrac{-x}{\sqrt{x^2+y^2}} \right) \right]\;\mathbf{k}\\ & \\ =& 0\,\mathbf{i} - 0 \,\mathbf{j} + \left( \dfrac{-2xy}{x^2+y^2} - \dfrac{-2xy}{x^2+y^2} \right) \,\mathbf{k}\\ =& 0\,\mathbf{i} - 0 \,\mathbf{j} + 0 \,\mathbf{k} \end{align*} \]

Exemplo 02

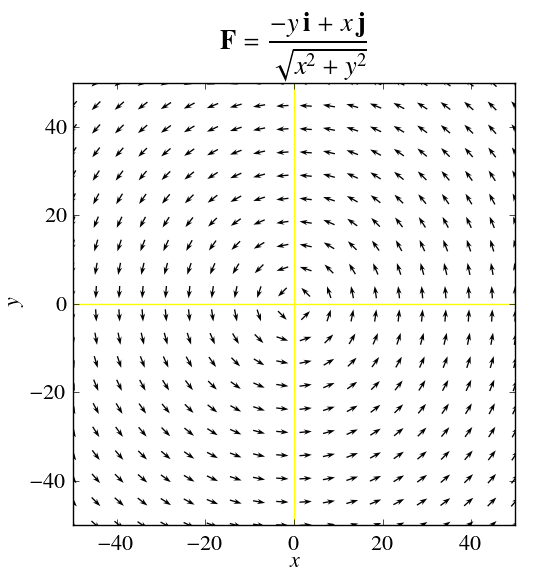
Calcule o campo rotacional de $\displaystyle \mathbf{F} = \dfrac{-y\,\mathbf{i} + x \,\mathbf{j}}{\sqrt{x^2+y^2}}$
SOL.

\[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ \dfrac{-y}{\sqrt{x^{2}+y^{2}}} & \dfrac{x}{\sqrt{x^{2}+y^{2}}} & 0 \end{bmatrix}\\ \\ = & \left[\dfrac{\partial\;}{\partial y}0-\dfrac{\partial\;}{\partial z}\left(\dfrac{x}{\sqrt{x^{2}+y^{2}}}\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}0-\dfrac{\partial\;}{\partial z}\left(\dfrac{-y}{\sqrt{x^{2}+y^{2}}}\right)\right]\;\mathbf{j}+\\ & \left[\dfrac{\partial\;}{\partial x}\left(\dfrac{x}{\sqrt{x^{2}+y^{2}}}\right)-\dfrac{\partial\;}{\partial y}\left(\dfrac{-y}{\sqrt{x^{2}+y^{2}}}\right)\right]\;\mathbf{k}\\ \\ = & 0\,\mathbf{i}-0\,\mathbf{j}+\left(\dfrac{\left(x^{2}+y^{2}\right)^{\frac{1}{2}}-x^{2}\left(x^{2}+y^{2}\right)^{-\frac{1}{2}}}{x^{2}+y^{2}}+\dfrac{\left(x^{2}+y^{2}\right)^{\frac{1}{2}}-y^{2}\left(x^{2}+y^{2}\right)^{-\frac{1}{2}}}{x^{2}+y^{2}}\right)\,\mathbf{k}\\ = & 0\,\mathbf{i}-0\,\mathbf{j}-\left[\dfrac{x^{2}+y^{2}-x^{2}+x^{2}+y^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{3/2}}\right]\,\mathbf{k}\\ = & 0\,\mathbf{i}-0\,\mathbf{j}-\dfrac{y^{2}+x^{2}}{\left(x^{2}+y^{2}\right)^{3/2}}\,\mathbf{k}\\ = & 0\,\mathbf{i}-0\,\mathbf{j}-\dfrac{1}{\sqrt{x^{2}+y^{2}}}\,\mathbf{k} \end{align*} \]

Exemplo 03

Calcule o campo rotacional de $\displaystyle \mathbf{F} = \dfrac{-y\,\mathbf{i} + x \,\mathbf{j}}{x^2+y^2}$
SOL.

\[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ \dfrac{-y}{x^{2}+y^{2}} & \dfrac{x}{x^{2}+y^{2}} & 0 \end{bmatrix}\\ \\ = & \left[\dfrac{\partial\;}{\partial y}0-\dfrac{\partial\;}{\partial z}\left(\dfrac{x}{x^{2}+y^{2}}\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}0-\dfrac{\partial\;}{\partial z}\left(\dfrac{-y}{x^{2}+y^{2}}\right)\right]\;\mathbf{j}+\\ & \left[\dfrac{\partial\;}{\partial x}\left(\dfrac{x}{x^{2}+y^{2}}\right)-\dfrac{\partial\;}{\partial y}\left(\dfrac{-y}{x^{2}+y^{2}}\right)\right]\;\mathbf{k}\\ \\ = & 0\,\mathbf{i}-0\,\mathbf{j}+\left[\dfrac{\left(x^{2}+y^{2}\right)-2x^{2}}{\left(x^{2}+y^{2}\right)^{2}}+\dfrac{\left(x^{2}+y^{2}\right)-2y^{2}}{\left(x^{2}+y^{2}\right)^{2}}\right]\,\mathbf{k}\\ = & 0\,\mathbf{i}-0\,\mathbf{j}-\left(\dfrac{-x^{2}+y^{2}+x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}\right)\,\mathbf{k}\\ = & 0\,\mathbf{i}-0\,\mathbf{j}-0\,\mathbf{k} \end{align*} \]

Exemplo 04

Calcule o campo rotacional de $\displaystyle \mathbf{F} = \dfrac{-x\,\mathbf{i} -y \,\mathbf{j}}{\sqrt{x^2+y^2}}$
SOL.

\[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ \dfrac{x}{\sqrt{x^{2}+y^{2}}} & \dfrac{-y}{\sqrt{x^{2}+y^{2}}} & 0 \end{bmatrix}\\ \\ = & \left[\dfrac{\partial\;}{\partial y}0-\dfrac{\partial\;}{\partial z}\left(\dfrac{-y}{\sqrt{x^{2}+y^{2}}}\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}0-\dfrac{\partial\;}{\partial z}\left(\dfrac{x}{\sqrt{x^{2}+y^{2}}}\right)\right]\;\mathbf{j}+\\ & \left[\dfrac{\partial\;}{\partial x}\left(\dfrac{-y}{\sqrt{x^{2}+y^{2}}}\right)-\dfrac{\partial\;}{\partial y}\left(\dfrac{x}{\sqrt{x^{2}+y^{2}}}\right)\right]\;\mathbf{k}\\ \\ = & 0\,\mathbf{i}-0\,\mathbf{j}+\left(\dfrac{yx\left(x^{2}+y^{2}\right)^{-\frac{1}{2}}}{x^{2}+y^{2}}-\dfrac{-xy\left(x^{2}+y^{2}\right)^{-\frac{1}{2}}}{x^{2}+y^{2}}\right)\,\mathbf{k}\\ = & 0\,\mathbf{i}-0\,\mathbf{j}-\left[\dfrac{2xy}{\left(x^{2}+y^{2}\right)^{3/2}}\right]\,\mathbf{k} \end{align*} \]

Exemplo 05

Um escoamento é representado pelo campo de velocidades $\displaystyle \mathbf{v} = 10x\,\mathbf{i} - 10y \,\mathbf{j} + 30 \,\mathbf{k}$, verifique (a) Se há um escoamento incompressível. (b) Se há um escoamento irrotacional.
SOL.
Para termos um escoamento incompressível devemos verificar que a divergência do campo seja nula, \[ \begin{align*} \vec{\nabla}\cdot\vec{v}= & \left(\dfrac{\partial\;}{\partial x}\,\mathbf{i}+\dfrac{\partial\;}{\partial y}\,\mathbf{j}+\dfrac{\partial\;}{\partial z}\,\mathbf{k}\right)\cdot\left(\mathbf{v}=10x\,\mathbf{i}-10y\,\mathbf{j}+30\,\mathbf{k}\right)\\ = & \dfrac{\partial\;}{\partial x}\left(10x\right)+\dfrac{\partial\;}{\partial y}\left(-10y\right)+\dfrac{\partial\;}{\partial z}\left(30\right)\\ = & 10-10\\ = & 0 \end{align*} \] por tanto temos um escoamento incompressível. Agora devemos verificar que o rotacional do campo é nulo, \[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ 10x & -10y & 30 \end{bmatrix}\\ = & \left[\dfrac{\partial\;}{\partial y}\left(30\right)-\dfrac{\partial\;}{\partial z}\left(10y\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}\left(30\right)-\dfrac{\partial\;}{\partial z}\left(10x\right)\right]\;\mathbf{j}+\\ = & \left[\dfrac{\partial\;}{\partial x}\left(10y\right)-\dfrac{\partial\;}{\partial z}\left(10x\right)\right]\;\mathbf{k}\\ = & \vec{0} \end{align*} \]

Exemplo 06

O campo eletrostático associado a uma carga positiva $Q$ é dado pela equação $\displaystyle \mathbf{E}=\vec{\nabla}\,V$, onde $\displaystyle V=\dfrac{Q}{r}$, sendo $\displaystyle r=\sqrt{x^2+y^2}$, verificar que o campo $\mathbf{E}$ é irrotacional

SOL.
\[ \begin{align*} \mathbf{E}= & \vec{-\nabla}\, V\\ = & -\left(\dfrac{\partial\;}{\partial x}\,\mathbf{i}+\dfrac{\partial\;}{\partial y}\,\mathbf{j}\right)V\\ = & -\dfrac{\partial V}{\partial x}\,\mathbf{i}-\dfrac{\partial V}{\partial y}\,\mathbf{j}\\ = & -\dfrac{\partial\;}{\partial x}\left(\dfrac{Q}{\sqrt{x^{2}+y^{2}}}\right)\,\mathbf{i}-\dfrac{\partial\;}{\partial y}\left(\dfrac{Q}{\sqrt{x^{2}+y^{2}}}\right)\,\mathbf{j}\\ = & \dfrac{\frac{1}{2}Q\left(x^{2}+y^{2}\right)^{-\frac{1}{2}}\left(2x\right)}{x^{2}+y^{2}}\mathbf{\, i}+\dfrac{\frac{1}{2}Q\left(x^{2}+y^{2}\right)^{-\frac{1}{2}}\left(2y\right)}{x^{2}+y^{2}}\mathbf{\, j}\\ = & \dfrac{Qx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}\mathbf{\, i}+\dfrac{Qy}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}\mathbf{\, j}\\ = & \dfrac{Q}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}\left(x\mathbf{\, i}+y\mathbf{\, j}\right)\\ = & \dfrac{Q}{x^{2}+y^{2}}\left(\dfrac{x\mathbf{\, i}+y\mathbf{\, j}}{\sqrt{x^{2}+y^{2}}}\right)\\ = & \dfrac{Q}{x^{2}+y^{2}}\hat{r} \end{align*} \] dessa forma o rotacional está dado por \[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ \dfrac{Qx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}} & \dfrac{Qy}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}} & 0 \end{bmatrix}\\ = & \left[\dfrac{\partial\;}{\partial y}\left(0\right)-\dfrac{\partial\;}{\partial z}\left(\dfrac{Qy}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}\left(0\right)-\dfrac{\partial\;}{\partial z}\left(\dfrac{Qx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}\right)\right]\;\mathbf{j}+\\ = & \left[\dfrac{\partial\;}{\partial x}\left(\dfrac{Qy}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}\right)-\dfrac{\partial\;}{\partial y}\left(\dfrac{Qx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}\right)\right]\;\mathbf{k}\\ = & 0\;\mathbf{i}+0\;\mathbf{j}+\left[-\dfrac{3Qyx}{\left(x^{2}+y^{2}\right)^{2}}+\dfrac{3Qyx}{\left(x^{2}+y^{2}\right)^{2}}\right]\;\mathbf{k}\\ = & \mathbf{0} \end{align*} \]

Exemplo 07

Seja $R=\left\{ (x,y)\, \left| \, 4 < x^2 + y^2 < 16 \right. \right\}$ é um domínio conexo mas não simples.
SOL.
Na figura embaixo se apresenta uma reprodução da Região $R$

Dentro dessa figura tracejamos uma linha pontilhada branca, nosso desejo é tentar colapsar essa linha até o ponto central preto sem sairmos da região $R$, mas como você pode observar isso nunca será possível, por tanto a nossa região não é simplesmente conexa.

Exemplo 08

O interior de uma esfera com um número finito de pontos é um domínio simplesmente conexo.

SOL.
Na figura embaixo se apresenta uma reprodução da Região $R$

Suponha que desejamos colapsar a curva tracejada branca ao ponto verde,mas a função não está definida no ponto vermelho. Como é permitida qualquer modificação da curva tracejada nos propomos levantar ela até tirar do plano onde estão os pontos (seguindo a linha laranja) e então colapsar a curva, dessa forma livramos o ponto vermelho. Isto só é possível porque a região $R$ está definida em $\mathbb{R}^3$.

Exemplo 09

O interior de um cubo onde foi removida uma diagonal não é uma região simplesmente conexa.

SOL.
Na figura embaixo se apresenta uma reprodução da Região $R$

Ao removermos uma linha inteira (infinitos pontos do cubo) nos não temos como contornar ela, a elipse que desejamos contrair até o ponto verde sempre ficará pressa na linha vermelha.

Exemplo 10

É o campo vetorial $\displaystyle \mathbf{F} = 2x^2y \,\mathbf{i} + 5xz \,\mathbf{j} + x^2 y^2 \,\mathbf{k}$ definido em $\mathbb{R}^3$ um campo que deriva de um gradiente e/ou um campo conservativo?

SOL.
Para ser um campo conservativo deve verificar que o domínio é simplesmente conexo e em se tratando de polinômios isto é verdade e além disso o seu rotacional deve ser nulo: \[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ 2x^{2}y & 5xz & x^{2}y^{2} \end{bmatrix}\\ = & \left[\dfrac{\partial\;}{\partial y}\left(x^{2}y^{2}\right)-\dfrac{\partial\;}{\partial z}\left(5xz\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}\left(x^{2}y^{2}\right)-\dfrac{\partial\;}{\partial z}\left(2x^{2}\right)\right]\;\mathbf{j}+\\ = & \left[\dfrac{\partial\;}{\partial x}\left(5xz\right)-\dfrac{\partial\;}{\partial y}\left(2x^{2}\right)\right]\;\mathbf{k}\\ = & \left(2x^{2}y-5x\right)\;\mathbf{i}+2xy^{2}\;\mathbf{j}+5z\;\mathbf{k} \end{align*} \] por tanto não é um campo conservativo.

Exemplo 11

É o campo vetorial $\displaystyle \mathbf{F} =\left( 4xy + z \right) \,\mathbf{i} + 2x^2 \,\mathbf{j} + x \,\mathbf{k}$ definido em $\mathbb{R}^3$, um campo conservativo?

SOL.
Para ser um campo conservativo deve verificar que o domínio é simplesmente conexo e em se tratando de polinômios isto é verdade e além disso o seu rotacional deve ser nulo: \[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ 4xy+z & 2x^{2} & x \end{bmatrix}\\ = & \left[\dfrac{\partial\;}{\partial y}\left(x\right)-\dfrac{\partial\;}{\partial z}\left(2x^{2}\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}\left(x\right)-\dfrac{\partial\;}{\partial z}\left(4xy+z\right)\right]\;\mathbf{j}+\\ = & \left[\dfrac{\partial\;}{\partial x}\left(2x^{2}\right)-\dfrac{\partial\;}{\partial y}\left(4xy+z\right)\right]\;\mathbf{k}\\ = & 0\;\mathbf{i}+0\;\mathbf{j}+0\;\mathbf{k} \end{align*} \] por tanto é um campo conservativo.

Exemplo 11

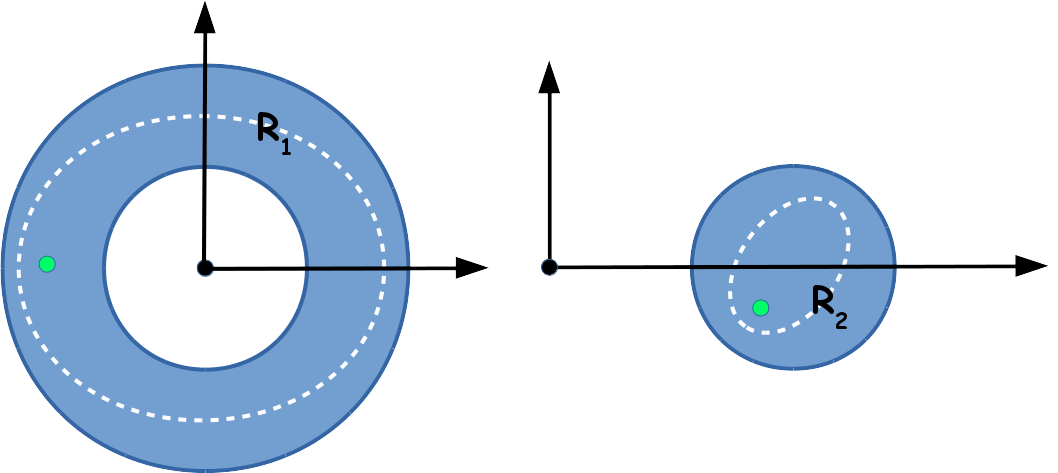
É o campo vetorial $\displaystyle \mathbf{F} = \dfrac{-y}{x^2 + y^2}\,\mathbf{i} + \dfrac{x}{x^2 + y^2} \,\mathbf{j}$ definido em $R_1 = \left\{ (x,\, y)\left| (x-3)^2 + y^2 < 1 \right. \right\}$ e $R_2 = \left\{ (x,\, y)\left| 1 < x^2 + y^2 < 16 \right. \right\}$, um campo conservativo.

SOL.
Como o campo foi definido em duas regiões primeiro verificaremos que o rotacional é nulo (ver problema 3), assim \[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ \dfrac{-y}{x^{2}+y^{2}} & \dfrac{x}{x^{2}+y^{2}} & 0 \end{bmatrix}\\ \\ = & \left[\dfrac{\partial\;}{\partial y}0-\dfrac{\partial\;}{\partial z}\left(\dfrac{x}{x^{2}+y^{2}}\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}0-\dfrac{\partial\;}{\partial z}\left(\dfrac{-y}{x^{2}+y^{2}}\right)\right]\;\mathbf{j}+\\ & \left[\dfrac{\partial\;}{\partial x}\left(\dfrac{x}{x^{2}+y^{2}}\right)-\dfrac{\partial\;}{\partial y}\left(\dfrac{-y}{x^{2}+y^{2}}\right)\right]\;\mathbf{k}\\ \\ = & 0\,\mathbf{i}-0\,\mathbf{j}+\left[\dfrac{\left(x^{2}+y^{2}\right)-2x^{2}}{\left(x^{2}+y^{2}\right)^{2}}+\dfrac{\left(x^{2}+y^{2}\right)-2y^{2}}{\left(x^{2}+y^{2}\right)^{2}}\right]\,\mathbf{k}\\ = & 0\,\mathbf{i}-0\,\mathbf{j}-\left(\dfrac{-x^{2}+y^{2}+x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}\right)\,\mathbf{k}\\ = & 0\,\mathbf{i}-0\,\mathbf{j}-0\,\mathbf{k} \end{align*} \] Agora devemos verificar que as regiões são simplesmente conexas. Observe que a função $\mathbf{F}$ está bem definida em $D\left[ \mathbf{F} \right] = \mathbb{R}^2 - \{0,0\}$. Dessa forma, no caso da região \[ R_1 = \left\{ (x,\, y)\left| (x-3)^2 + y^2 < 1 \right. \right\} \nonumber \] vemos que ela define um circulo de raio unitário centrado em $(3,0)$, por tanto a singularidade não está dentro da região e dessa forma o campo é conservativo. Já no caso da região \[ R_2 = \left\{ (x,\, y)\left| 1 < x^2 + y^2 < 16 \right. \right\} \nonumber \] Define um anel centrado em zero de raio interno $1$ e externo $4$. Essa região não é uma região simplesmente conexa pois podemos definir circunferências dentro do anel que não poderão ser colapsadas a único ponto.

Isso fica bem evidente na figura acima, observe que não é possível acessar o ponto em verde definido na região $R_1$ sem sair da região em questão.

Exemplo 12

Verificar se \[ \mathbf{F}(x,y,z) = \left( yz+2 \right)\,\mathbf{i} + \left( xz+1 \right) \,\mathbf{j} + \left( xy + 2z \right) \,\mathbf{k} \nonumber \] é um campo gradiente, em caso afirmativo encontre a função potencial.
SOL.
Saberemos que $\mathbf{F}$ é um campo gradiente se verificar $\vec{\nabla}\times\mathbf{F}=0$, por tanto Saberemos que $\mathbf{F}$ é um campo gradiente se verificar $\vec{\nabla}\times\mathbf{F}=0$, por tanto \[ \begin{align*} \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ F_{x} & F_{y} & F_{z} \end{bmatrix} & =0\\ \left[\dfrac{\partial F_{z}}{\partial y}-\dfrac{\partial F_{y}}{\partial z}\right]\;\mathbf{i}-\left[\dfrac{\partial F_{z}}{\partial x}-\dfrac{\partial F_{x}}{\partial z}\right]\;\mathbf{j}+\left[\dfrac{\partial F_{y}}{\partial x}-\dfrac{\partial F_{x}}{\partial y}\right]\;\mathbf{k} & =0 \end{align*} \] de onde \[ \begin{array}{r} \dfrac{\partial F_{z}}{\partial y}=\dfrac{\partial F_{y}}{\partial z}\\ \dfrac{\partial F_{z}}{\partial x}=\dfrac{\partial F_{x}}{\partial z}\\ \dfrac{\partial F_{y}}{\partial x}=\dfrac{\partial F_{x}}{\partial y} \end{array} \nonumber \] assim, então \[ \begin{array}{lcrcc} \dfrac{\partial\;}{\partial y}\left(xy+2z\right) & = & \dfrac{\partial\;}{\partial z}\left(xz+1\right) & = & x\\ \dfrac{\partial\;}{\partial x}\left(xy+2z\right) & = & \dfrac{\partial\;}{\partial z}\left(yz+2\right) & = & y\\ \dfrac{\partial\;}{\partial x}\left(xz+1\right) & = & \dfrac{\partial\;}{\partial y}\left(yz+2\right) & = & z \end{array} \nonumber \] dessa forma, a função vetorial $\mathbf{F}(x,y,z)$ deriva de um gradiente, isto é \[ \mathbf{F}(x,y,z)=\vec{\nabla f} \nonumber \] o que implica \[ \begin{align*} \dfrac{\partial f}{\partial x}= & F_{x}\\ \dfrac{\partial f}{\partial y}= & F_{y}\\ \dfrac{\partial f}{\partial z}= & F_{z} \end{align*} \] escolhamos a primeira dessa equações para resolver, pelo I teorema fundamental do cálculo \[ \begin{align*} f= & \int F_{x}dx\\ = & \int\left(yz+2\right)\, dx\\ = & xyz+2x+C_{1}(y,z) \end{align*} \] derivando a expressão anterior \[ \dfrac{\partial f}{\partial y}=xz+\dfrac{\partial C_{1}}{\partial y}=F_{y} \nonumber \] obtemos \[ \begin{align*} xz+\dfrac{\partial C_{1}}{\partial y}= & xz+1\\ \dfrac{\partial C_{1}}{\partial y}= & 1\\ C_{1}= & \int dy\\ = & y+C_{2}(z) \end{align*} \] de forma que \[ f=xyz+2x+y+C_{2}(z) \nonumber \] derivando \[ \dfrac{\partial f}{\partial z}=xy+\dfrac{\partial C_{2}}{\partial z}=F_{z} \nonumber \] substituindo $F_{z}$ \[ \begin{align*} xy+\dfrac{\partial C_{2}}{\partial z}= & xy+2z\\ \dfrac{\partial C_{2}}{\partial z}= & 2z\\ C_{2}= & 2\int z\, dz\\ = & z^{2}+C \end{align*} \] assim \[ f=xyz+2x+y+z^{2}+C \nonumber \]

Exemplo 13

Considere o campo vetorial $\mathbf{F}$ em $\mathbb{R}^3$ definido por \[ \mathbf{F}(x,y,z) = y\,\mathbf{i} + \left( z\cos yz + x\right) \,\mathbf{j} + \left( y\cos yz \right)\,\mathbf{k} \nonumber \] mostre que $\mathbf{F}$ é irrotacional e encontre um potencial escalar
SOL.
\[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ y & z\cos\left(yz\right)+x & y\cos\left(yz\right) \end{bmatrix}\\ = & \left[\dfrac{\partial\;}{\partial y}\left(y\cos\left(yz\right)+x\right)-\dfrac{\partial\;}{\partial z}\left(z\cos\left(yz\right)\right)\right]\;\mathbf{i}-\left[\dfrac{\partial\;}{\partial x}\left(y\cos\left(yz\right)+x\right)-\dfrac{\partial\;}{\partial z}\left(y\right)\right]\;\mathbf{j}+\\ = & \left[\dfrac{\partial\;}{\partial x}\left(z\cos\left(yz\right)\right)-\dfrac{\partial\;}{\partial y}\left(y\right)\right]\;\mathbf{k}\\ = & \left[z\cos\left(yz\right)-z\cos\left(yz\right)\right]\;\mathbf{i}+\left[0-0\right]\;\mathbf{j}+\left[1-1\right]\;\mathbf{k}\\ = & 0 \end{align*} \] por tanto deriva de um gradiente. Assim, calculamos o campo escalar \[ \begin{align*} f= & \int y\, dx\\ = & xy+C_{2}(x,y) \end{align*} \] \[ \begin{align*} \dfrac{\partial f}{\partial y} & =x+\dfrac{\partial C_{2}}{\partial y} \end{align*} \] de onde \[ \begin{align*} x+\dfrac{\partial C_{2}}{\partial y}= & z\cos\left(yz\right)+x\\ C_{2}= & \int z\,\cos\left(yz\right)\, dy\\ = & \sin\left(yz\right)+C_{1}(z) \end{align*} \] de forma \[ f=xy+\sin\left(yz\right)+C_{1}(z) \nonumber \] derivando \[ \dfrac{\partial f}{\partial z}=y\cos\left(yz\right)+\dfrac{\partial C_{1}}{\partial z}=y\cos\left(yz\right) \nonumber \] de onde \[ \dfrac{\partial C_{1}}{\partial z}=0\Rightarrow C_{1}=C \nonumber \] dessa forma \[ f=xy+\sin\left(yz\right)+C \nonumber \]

Exemplo 14

A massa $M$ na origem de $\mathbb{R}^3$ exerce uma força sobre uma massa $m$ localizada em $\mathbf{r}=(x,y,z)$ com magnitude $\dfrac{GMm}{r^2}$ em direção à origem. Aqui, $G$ é a constante de gravitação, a qual depende da unidade de medida utilizada, e $r=|\, \mathbf{r} \, |=\sqrt{x^2 + y^2 + z^2}$. Como o vetor $-\dfrac{\mathbf{r}}{r}$ é o vetor unitário em direção à origem, então podemos escrever \[ \mathbf{F}(x,y,z) = -\dfrac{GMm \mathbf{r}}{r^3} \nonumber \] Mostre que $\mathbf{F}$ é irrotacional e encontre o potencial escalar para $\mathbf{F}$ (note que $D\left[\mathbf{F}\right] = \mathbb{R}^3-(0,0,0)$ pois $\mathbf{F}$ não está definido na origem, mas mesmo assim o domínio é simplesmente conexo).
SOL.
Podemos reescrever a equação com \[ \mathbf{F}(x,y,z)=-\dfrac{GMm\mathbf{r}}{r^{3}}=-GMm\left(\dfrac{1}{r^{3}}\right)\mathbf{r} \nonumber \] aplicando o rotacional \[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \vec{\nabla}\times\left[-GMm\left(\dfrac{1}{r^{3}}\right)\mathbf{r}\right]\\ = & -GMm\left[\vec{\nabla}\left(\dfrac{1}{r^{3}}\right)\times\mathbf{r}+\left(\dfrac{1}{r^{3}}\right)\vec{\nabla}\times\mathbf{r}\right] \end{align*} \] dessa forma devemos calcular o gradiente \[ \begin{align*} \vec{\nabla}\left(\dfrac{1}{r^{3}}\right)= & \left[\dfrac{\partial\;}{\partial x}\;\mathbf{i}+\dfrac{\partial\;}{\partial y}\;\mathbf{j}+\dfrac{\partial\;}{\partial z}\;\mathbf{k}\right]\left(\dfrac{1}{\left(x^{2}+y^{2}+z^{2}\right)^{3/2}}\right)\\ = & \dfrac{3x\left(x^{2}+y^{2}+z^{2}\right)^{1/2}}{\left(x^{2}+y^{2}+z^{2}\right)^{3}}\;\mathbf{i}+\dfrac{3y\left(x^{2}+y^{2}+z^{2}\right)^{1/2}}{\left(x^{2}+y^{2}+z^{2}\right)^{3}}\;\mathbf{j}+\dfrac{3z\left(x^{2}+y^{2}+z^{2}\right)^{1/2}}{\left(x^{2}+y^{2}+z^{2}\right)^{3}}\;\mathbf{k}\\ = & \dfrac{3}{\left(x^{2}+y^{2}+z^{2}\right)^{5/2}}\left(x\;\mathbf{i}+y\;\mathbf{j}+z\;\mathbf{k}\right) \end{align*} \] \[ \begin{align*} \vec{\nabla}\left(\dfrac{1}{r^{3}}\right)\times\mathbf{r}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{3x}{\left(x^{2}+y^{2}+z^{2}\right)^{5/2}} & \dfrac{3y}{\left(x^{2}+y^{2}+z^{2}\right)^{5/2}} & \dfrac{3z}{\left(x^{2}+y^{2}+z^{2}\right)^{5/2}}\\ x & y & z \end{bmatrix}\\ = & \dfrac{3}{\left(x^{2}+y^{2}+z^{2}\right)^{5/2}}\left[\left(yz-yz\right)\;\mathbf{i}+\left(xz-xz\right)\;\mathbf{j}+\left(xy-xy\right)\;\mathbf{k}\right]\\ = & \vec{0} \end{align*} \] \[ \begin{align*} \vec{\nabla}\times\mathbf{r}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ x & y & z \end{bmatrix}\\ = & \left(0-0\right)\;\mathbf{i}-\left(0-0\right)\;\mathbf{j}+\left(0-0\right)\;\mathbf{k}\\ = & \vec{0} \end{align*} \] dessa forma \[ \vec{\nabla}\times\mathbf{F}=\vec{0} \nonumber \]