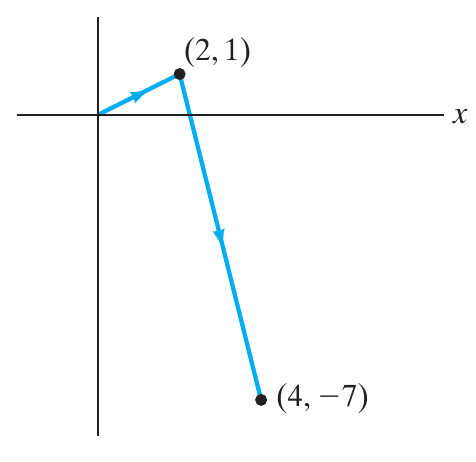Integral de linha de campos escalares

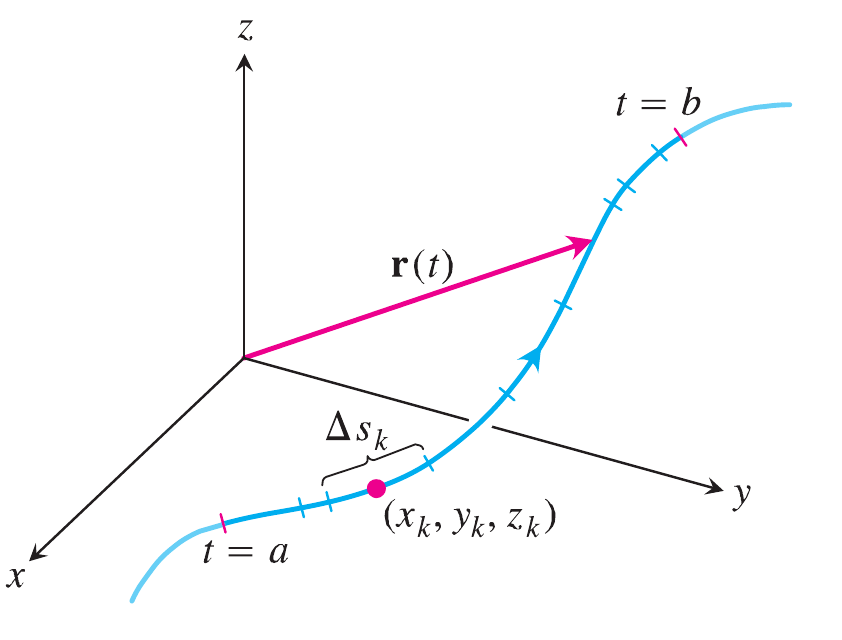
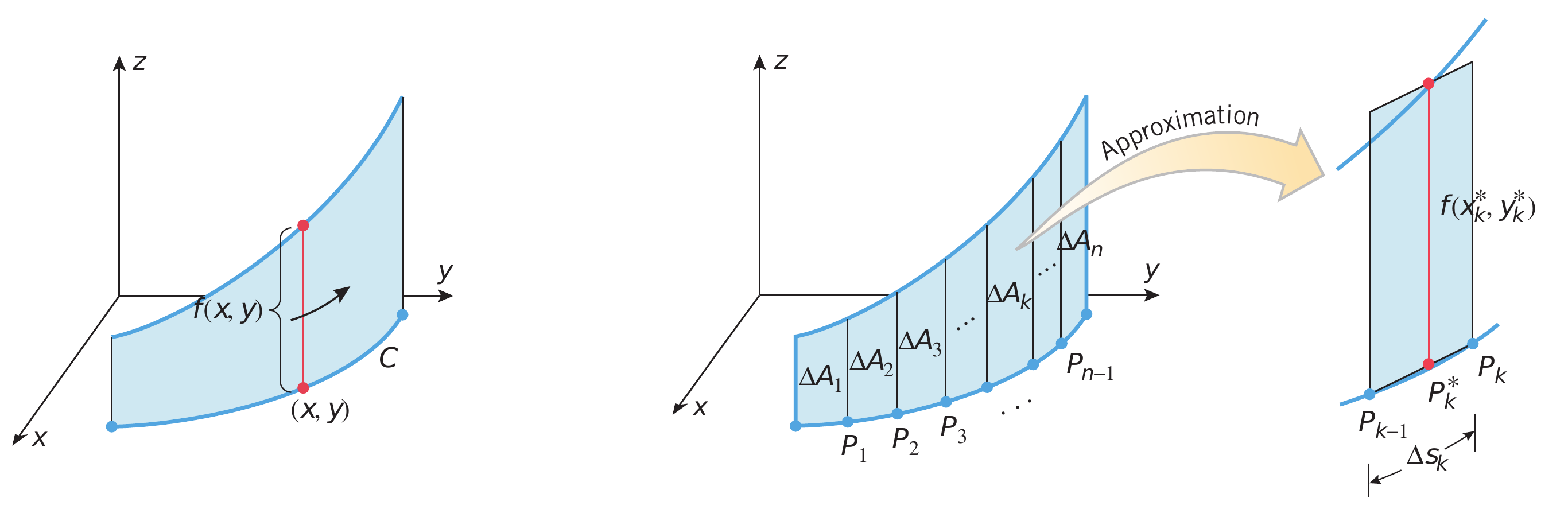
Suponhamos que desejamos calcular a massa de um fio, para isso teremos que saber algumas propriedades físicas do sistema, uma delas é a densidade linear de massa $\lambda\left(r(t)\right)$, a qual é uma função da posição. A outra é uma função $\mathbf{r}(t)$ que descreva cada ponto do fio, com isso \[ dm = \lambda\left(r(t)\right) \, ds \nonumber \] Nesta equação $dm$ é a massa infinitesimal de um pequeno segmento $ds$ do fio, tal como mostra a figura do lado. Por definição sabemos que qualquer elemento infinitesimal, $ds$, do fio está descrito pela equação \[ ds = |\, \mathbf{v} \,| dt \nonumber \] e a massa total será a soma de todas os pequenos elementos de massa \[ m = \int_{t_0}^t \lambda\left(r(t)\right)\,|\, \mathbf{v} \,| dt \nonumber \] A integrais similares à anterior chamamos de integrais de linha porque a integração é feita ao longo do caminho $ds$ descrito pela curva $\mathbf{r}(t)$. Em termos gerais podemos definir o conceito de integral de linha sem perda de generalidade como

Definição

A integral de linha escalar de um $f$ ao longo do caminho de classe $C^1$ definido por $\mathbf{r}$ está dada por \[ \int_C f\, ds = \int_{a}^b f\left( x(t),\, y(t),\, z(t) \right) \,|\, \mathbf{v} \,| dt \nonumber \] onde $\displaystyle \mathbf{r} = (x, y, z) $ e $\displaystyle \mathbf{v} = \dfrac{d \mathbf{r}}{dt}$

A continuação vamos listar as propriedades da integral de linha

Propriedades

Se $k$ é uma constante, então \[ \int_C k\,f(x,y,z)\,ds = k\int_C \,f(x,y,z)\,ds \nonumber \] $\displaystyle \int_C \left[\,f(x,y,z) + g(x,y,z)\right]\,ds = \int_C \,f(x,y,z)\,ds + \int_C \,g(x,y,z)\,ds$ Seja $C$ uma curva orientada que composta por várias curvas componentes: $C=C_1 + C_2 + \ldots + C_k$, então \[ \int_C \,f(x,y,z)\,ds = \int_{C_1} f(x,y,z)\,ds + \int_{C_2} f(x,y,z)\,ds + \ldots +\int_{C_k} f(x,y,z)\,ds \nonumber \] Seja $C^-$ a mesma curva que $C$, mas com orientação oposta, então \[ \int_C \,f(x,y,z)\,ds = \int_{C^-} \,f(x,y,z)\,ds \nonumber \]

Exemplo 01

Seja $f(x,y) = y -x$ e $C$ a curva definida pela função \[ \mathbf{r}(t) = \begin{cases} \left( 2t,\,t \right) & \text{se } 0 \leq t < 1\\ \left( t+1,\,5-4t \right) & \text{se } 1 < t \leq 3 \end{cases} \nonumber \]

Exemplo 02

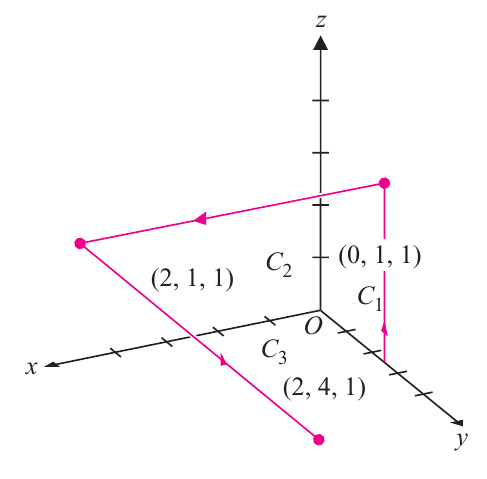
Calcule $\displaystyle \int_C 4x\,dy + 2y\,dz$, onde $C$ consiste do segmento de linha entre $(0,1,0)$ até $(0,1,1)$, seguido pelo segmento $(0,1,0)$ até $(2,1,1)$ e seguido pela linha $(2,1,1)$ até $(2,4,1)$

Exemplo 03

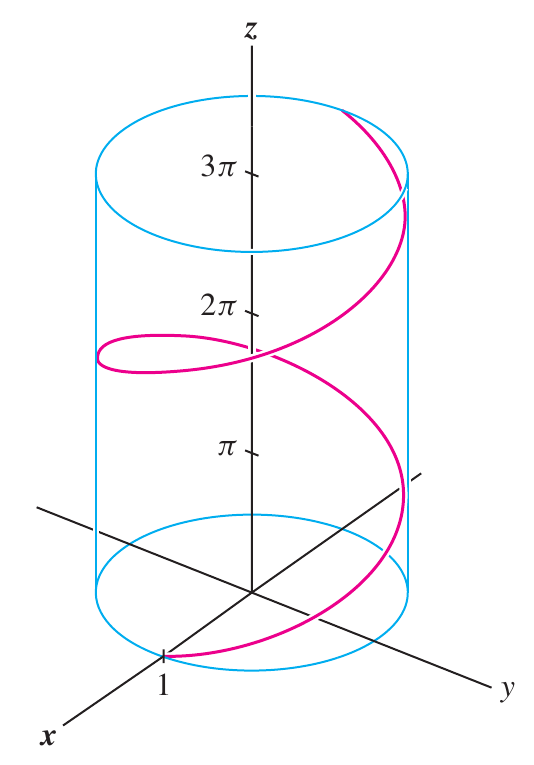
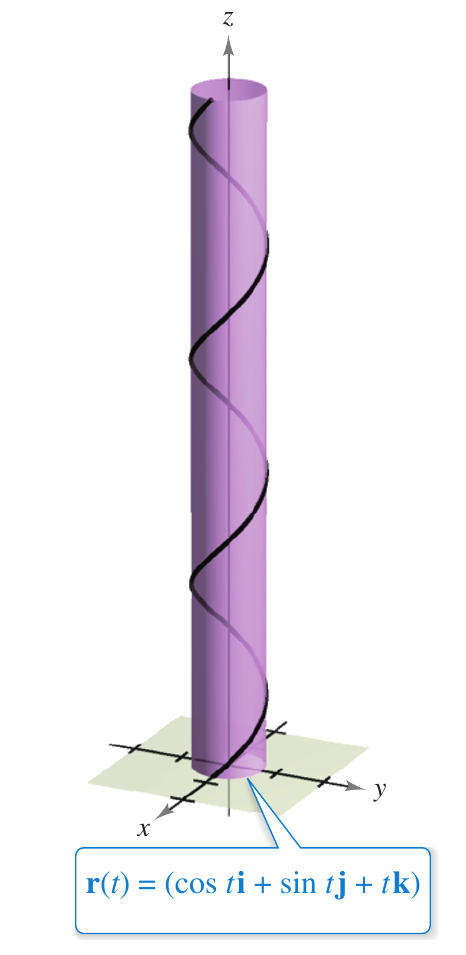
Calcule $\displaystyle \int_c \left( x+y+z \right)ds$, onde $C$ é a hélice re raio $1$ definido entre $0 \leq t\leq \pi$

Exemplo 04

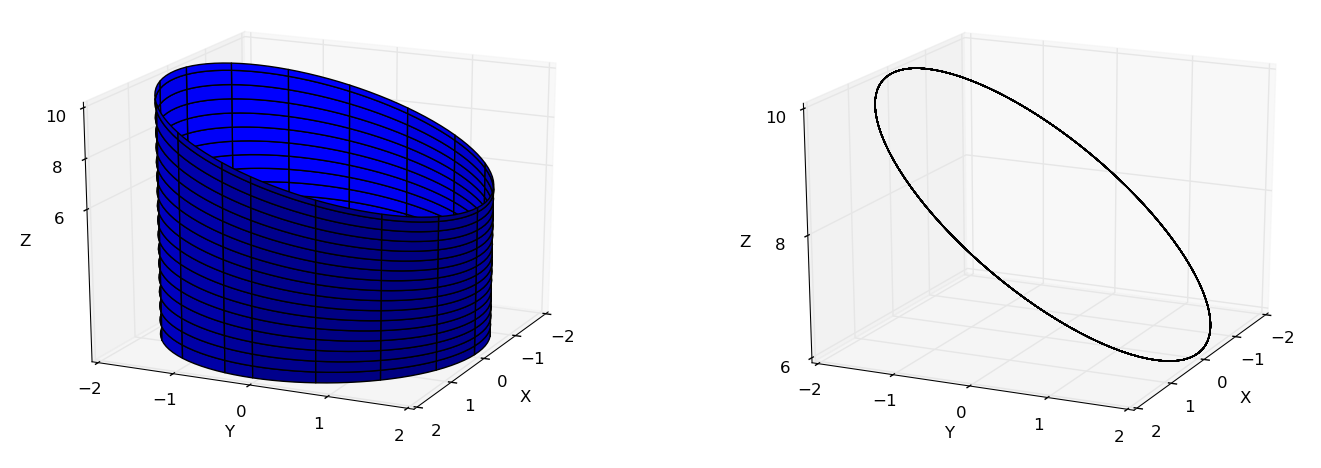
Calcular $\displaystyle \int_C xy\,ds$, onde $C$ é a interseção das superfícies $x^2+y^2=4$ e o plano $y+z=8$

Exemplo 05

Avalie a integral $\displaystyle \int_C x^2y\,ds$, onde $C$ está dada pela parametrização $\displaystyle \mathbf{r}(t) = 3\cos\,t\,\mathbf{i} + 3\sin \,t\,\mathbf{j}$, $0\leq t \leq \pi / 2$. Seguidamente mostre que se utilizamos a parametrização $\displaystyle \mathbf{r}(t) = \sqrt{9-y^2}\,\mathbf{i} + y \,\mathbf{j}$, $0\leq y \leq 3$, obteremos o mesmo resultado.

Aplicações da integral escalar de linha

Interpretação geométrica

Se a curva $C$ está em algum plano, suponhamos $xy$, e não negativa, então é fácil ver, como mostra a figura embaixo, que o produto do comprimento da curva pela função $f(x,y)$ é exatamente igual à área da "cortina" medida desde a $\mathbf{r}_1=(x,y,0)$ até a linha $\mathbf{r}_2=\left(x,y,f(x,y,z)\right)$

Dessa forma podemos escrever \[ A = \int_C f(x,y)\,ds \nonumber \]

Exemplo 06

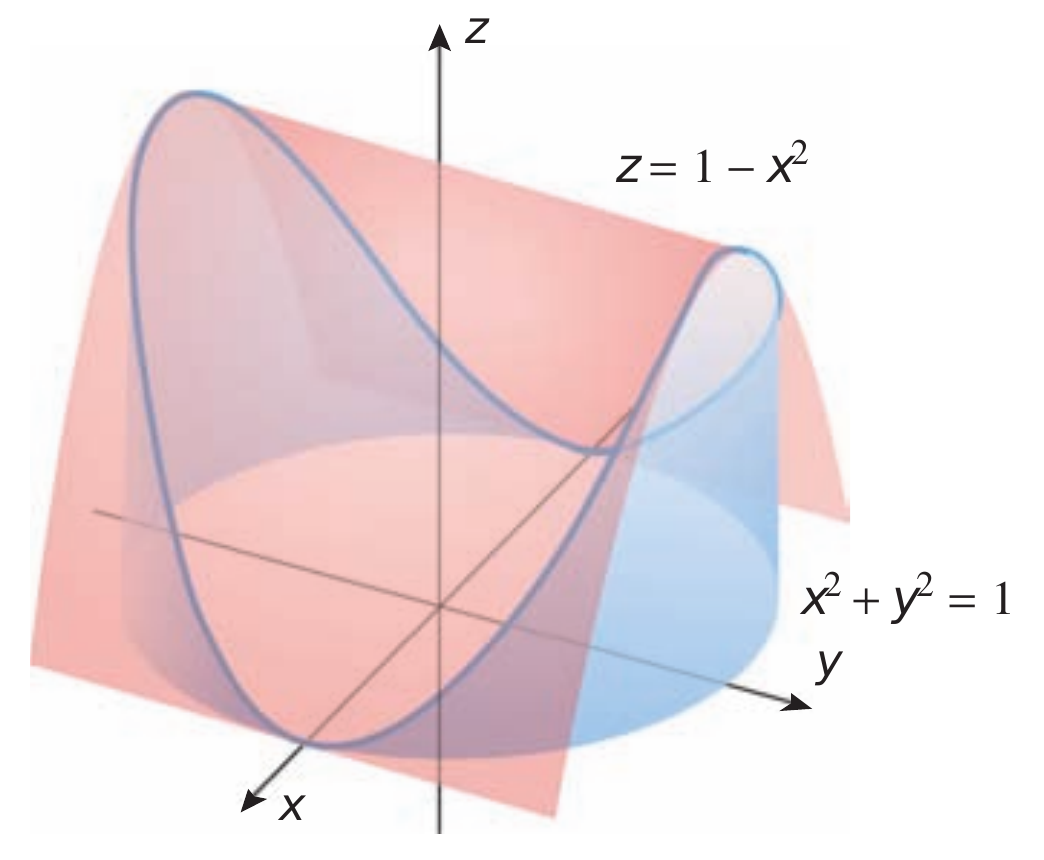
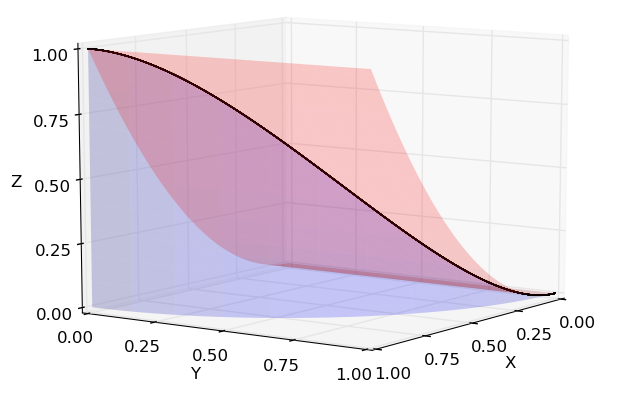
Calcule a área da superfície estendida para cima do círculo $x^2+y^2=1$ no plano $xy$ até a parábola cilíndrica $z=1-x^2$

Além do cálculo da massa da área de uma "cortina", a integral de linha pode ser utilizada para calcular:

Exemplo 07

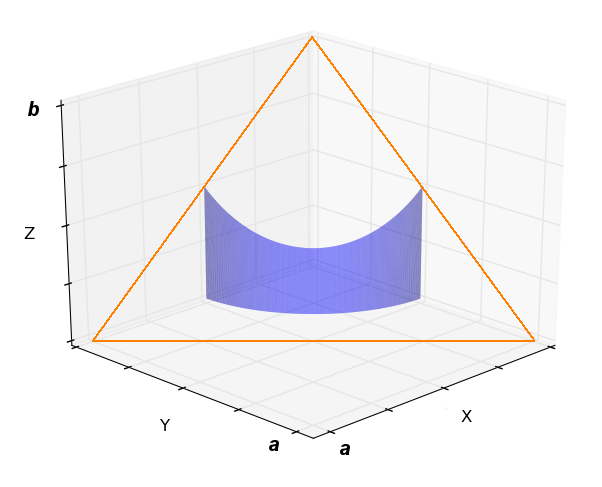
Imaginemos um teatro em forma de tetraedro, como aquele formado pelos planos coordenados e o plano $\displaystyle z = \dfrac{b}{a}\left( a-x-y \right)$, onde $b > a > 0$, de modo que sua base é um triangulo isósceles com vértice na origem e os ponto $(a,0,0)$ e $(0,a,0)$, e sua altura é $b$. O palco é circular e ocupa uma região $xy$ dada por $\{(x,y)\,|\, x^2+y^2 \leq r^2, \, x \geq 0, y \geq 0\}$, onde $r < \dfrac{\sqrt{3} a}{2}$. Como se quer colocar uma cortina desde o teto até a borda do palco, qual é a quantidade mínima de tecido que deve ser comprado?

Aplicações

Massa do fio: \[ m_f = \int_C \lambda (x,y,z)\,|\, \mathbf{v} \,| dt \nonumber \] Centro de massa do fio: \[ x_m = \dfrac{1}{m_f}\int_C x\lambda (x,y,z)\,|\, \mathbf{v} \,| dt \nonumber \] \[ y_m = \dfrac{1}{m_f}\int_C y\lambda (x,y,z)\,|\, \mathbf{v} \,| dt \nonumber \] \[ z_m = \dfrac{1}{m_f}\int_C z\lambda (x,y,z)\,|\, \mathbf{v} \,| dt \nonumber \] Momento de inercia: \[ I = \dfrac{1}{m_f}\int_C \rho^2\,\lambda (x,y,z)\,|\, \mathbf{v} \,| dt \nonumber \] onde $\rho$ é a distância desde o ponto até o eixo de rotação. Lei de Biot-Savart \[ B = k \int_C \dfrac{i_e\sin \theta}{r^2}\,|\, \mathbf{v} \,| dt \nonumber \] Potencial Elétrico \[ V(x,y,z) = k\int_C \dfrac{\lambda_e(x,y,z)\,ds }{r} \nonumber \] onde $r=|\, \mathbf{r} \,|$ = (x,y,z) e $\lambda_e(x,y,z)$ é a densidade linear de carga elétrica.

Exemplo 08

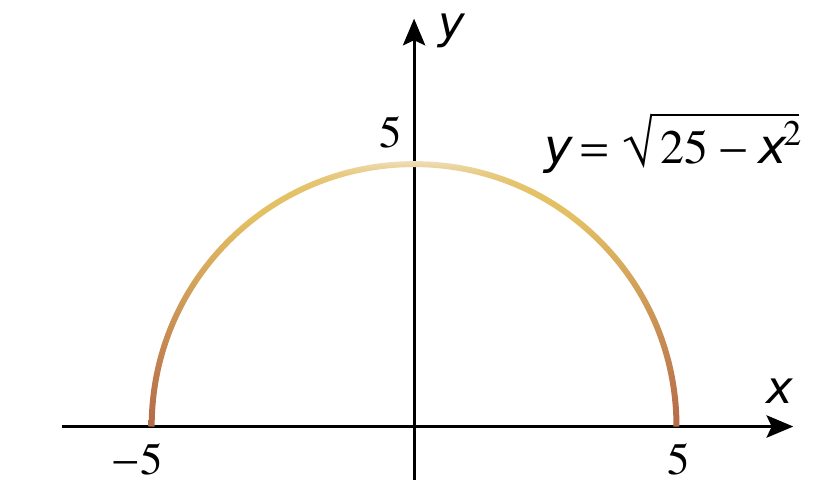
Suponha que um arame semicircular tenha a equação $y=\sqrt{25-x^2}$ e que sua densidade linear de massa seja $\lambda(x,y) = 15-y$. Fisicamente isso significa que o arame tem uma densidade máxima na base e decresce linearmente com o valor de $y$ para um valore de 15 unidades no topo ($y=5$). Calcule a massa total do arame

Exemplo 09

Calcule a Massa de um fio localizado no primeiro octante o qual é descrito pela interseção do paraboloide elíptico $z=2-x^2-2y^2$ e o cilindro parabólico $z=x^2$ entre os pontos $(0,1,0)$ e $(1,0,1)$ se a densidade linear de massa está dada por $\lambda = xy$

Exemplos 10

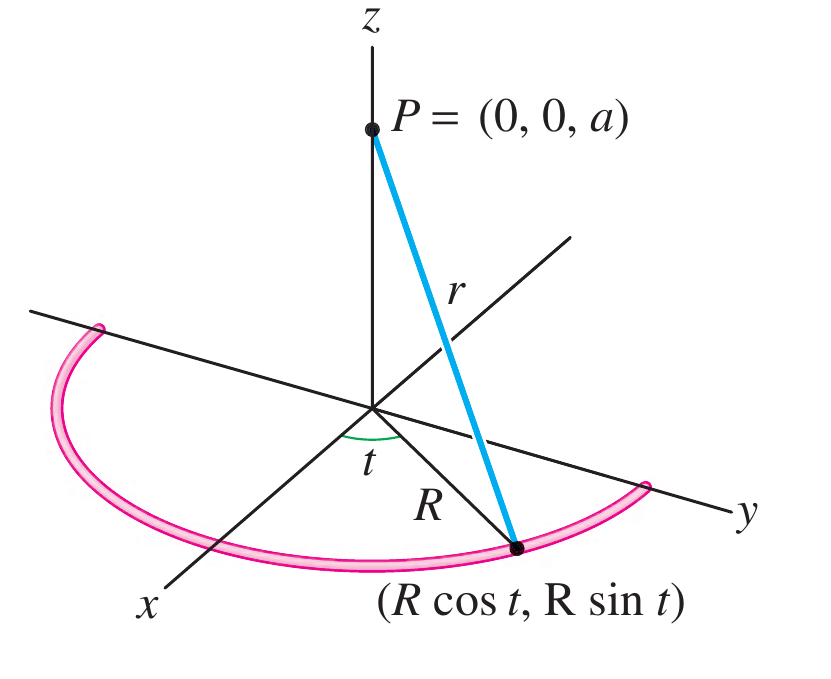
Um semicírculo carregado de raio $R$ centrado na origem no plano $xy$ tem densidade de carga linear \[ \lambda_e(x,y) = 1\times 10^{-8}\left( 2-\dfrac{x}{R} \right)\,C/m \nonumber \] Calcule o potencial elétrico no ponto $P=(0,0,a)$, se $R=0,1\,m$

Exemplos 11

Calcule o centro de massa do arame em forma de hélice $C:[0,2\pi]\to \mathbb{R}^3,\,\mathbf{r}(t)=\left( \cos\,t,\,\sin\, t,\,t \right)$, cuja função densidade de massa é $\lambda(x,y,z)=x^2+y^2+z^2$.