Exemplos sobre Integral de linha de campos vetoriais

Exemplo 01

Calcule a integral $\int_{C}\mathbf{F}\cdot d\mathbf{r}$, onde $\mathbf{F}=z\,\mathbf{i}+xy\,\mathbf{j}-y^{2}\,\mathbf{k}$ ao longo da curva dada por $\mathbf{r}(t)=t^{2}\,\mathbf{i}+t\,\mathbf{j}+\sqrt{t}\,\mathbf{k}$, $0\leq t\leq1$

SOL.

Temos \[ \mathbf{F}\left(\mathbf{r}(t)\right)=\sqrt{t}\,\mathbf{i}+t^{3}\,\mathbf{j}-t^{2}\,\mathbf{k} \nonumber \] e \[ \mathbf{v}(t)=2t\,\mathbf{i}+\mathbf{j}+\dfrac{1}{2\sqrt{t}}\,\mathbf{k} \nonumber \] de forma que \begin{align*} \int_{C}\mathbf{F}\left(\mathbf{r}(t)\right)\cdot d\mathbf{r}= & \int_{0}^{1}\mathbf{F}\left(\mathbf{r}(t)\right)\cdot\mathbf{v}(t)dt\\ = & \int_{0}^{1}\left(2t^{3/2}+t^{3}-\dfrac{1}{2}t^{3/4}\right)dt\\ = & \left[\left(\dfrac{2}{3}\right)\left(\dfrac{2}{5}t^{5/2}\right)+\dfrac{1}{4}t^{4}\right]_{0}^{1}\\ = & \dfrac{17}{20} \end{align*}

Exemplo 03

Calcule a integral $\int_{C}\mathbf{F}\cdot d\mathbf{r}$, onde $\mathbf{F}=z\,\mathbf{i}+y^{2}\,\mathbf{j}-x\,\mathbf{k}$ ao longo da curva dada por $\mathbf{r}(t)=\left(t+1\right)\,\mathbf{i}+e^{t}\,\mathbf{j}+t^{2}\,\mathbf{k}$, $0\leq t\leq2$

SOL.

Temos \[ \mathbf{F}\left(\mathbf{r}(t)\right)=t^{2}\,\mathbf{i}+e^{2t}\,\mathbf{j}-\left(t+1\right)\,\mathbf{k} \nonumber \] e \[ \mathbf{v}(t)=\mathbf{i}+e^{t}\,\mathbf{j}+2t\,\mathbf{k} \nonumber \] de forma que \begin{align*} \int_{C}\mathbf{F}\left(\mathbf{r}(t)\right)\cdot d\mathbf{r}= & \int_{0}^{2}\mathbf{F}\left(\mathbf{r}(t)\right)\cdot\mathbf{v}(t)dt\\ = & \int_{0}^{2}\left(e^{3t}+3t^{2}+2t\right)dt\\ = & \left[\dfrac{1}{3}d^{3t}+t^{3}+t^{2}\right]_{0}^{2}\\ = & \left(\dfrac{1}{3}e^{6}+8+4\right)-\dfrac{1}{3}\\ = & \dfrac{1}{3}\left(e^{6}+35\right) \end{align*}

Exemplo 03

eja $\mathbf{r}(t)=\sin t\,\mathbf{i}+\cos t\,\mathbf{j}+t\,\mathbf{k}$ com $0\leq t\leq2\pi$. Seja o campo vetorial definido por $\mathbf{F}=x\,\mathbf{i}+y\,\mathbf{j}+z\,\mathbf{k}$. Calcule $\int_{C}\mathbf{F}\cdot d\mathbf{r}$

SOL.

Temos \[ \mathbf{F}\left(\mathbf{r}(t)\right)=\sin t\,\mathbf{i}+\cos t\,\mathbf{j}+t\,\mathbf{k} \nonumber \] e \[ \mathbf{v}(t)=-\cos t\,\mathbf{i}+\sin t\,\mathbf{j}+\,\mathbf{k} \nonumber \] de forma que \begin{align*} \int_{C}\mathbf{F}\left(\mathbf{r}(t)\right)\cdot d\mathbf{r}= & \int_{0}^{2\pi}\mathbf{F}\left(\mathbf{r}(t)\right)\cdot\mathbf{v}(t)dt\\ = & \int_{0}^{2\pi}\left(-\cos t\,\sin t+\cos t\,\sin t+t\right)dt\\ = & \left[\dfrac{1}{2}t^{2}\right]_{0}^{2\pi}\\ = & 2\pi^{2} \end{align*}

Exemplo 04

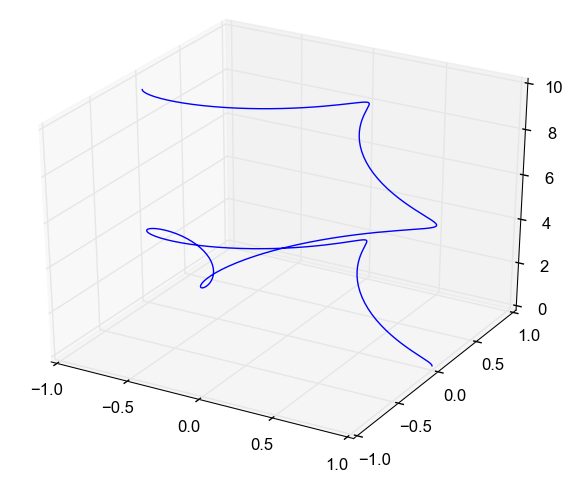
Seja $\mathbf{r}(t)=\cos^{3}t\,\mathbf{i}+\sin t\,\mathbf{j}+t\,\mathbf{k}$, onde $0\leq t\leq\dfrac{7}{2}\pi$, como se mostra na figura embaixo. Calcule a integral de linha $\int_{C}\left(\sin z\, dx+\cos z\, dy-\left(xy\right)^{1/3}dz\right)$

SOL.

Para este caso temos \[ \begin{align*} \dfrac{dx}{dt}= & -3\cos^{2}t\,\sin t\\ \dfrac{dy}{dt}= & 3\cos^{2}t\,\cos t\\ \dfrac{dz}{dt}= & 1 \end{align*} \] tal que a integral é \[ \begin{align*} \int_{C}\left(\sin z\, dx+\cos z\, dy-\left(xy\right)^{1/3}dz\right)= & -\int_{0}^{\frac{7\pi}{2}}3\sin t\,\cos^{2}t\,\sin t\, dt+\int_{0}^{\frac{7\pi}{2}}3\sin t\,\cos^{2}t\,\cos t\, dt-\int_{0}^{\frac{7\pi}{2}}\cos t\,\sin\, t\, dt\\ = & -\int_{0}^{\frac{7\pi}{2}}\cos t\,\sin\, t\, dt\\ = & -\left[\sin^{2}t\right]_{0}^{\frac{7\pi}{2}}\\ = & -\dfrac{1}{2} \end{align*} \]

Exemplo 05

Uma elipse orientada em sentido anti-horário é tem por parametrização $\mathbf{r}(t)=\left(5+4\cos t\right)\,\mathbf{i}+\left(3+2\cos t\right)\,\mathbf{j}$ onde $0\leq t\leq2\pi,$ calcule $\int_{C}2y\, dx-3\, dy$

SOL.

\[ \begin{align*} \dfrac{dx}{dt}= & -4\sin t\\ \dfrac{dy}{dt}= & 2\cos t \end{align*} \] assim \[ \begin{align*} \int_{C}2y\, dx-3\, dy= & 2\int_{0}^{2\pi}\left(3+2\sin t\right)\left(-4\sin t\right)\, dt-3\int_{0}^{2\pi}\left(2\cos t\right)\, dt\\ = & -24\int_{0}^{2\pi}\sin t\, dt-16\int_{0}^{2\pi}\sin^{2}t\, dt-3\int_{0}^{2\pi}\left(2\cos t\right)\, dt\\ = & -16\int_{0}^{2\pi}\sin^{2}t\, dt\\ = & -16\pi \end{align*} \]

Exemplo 06

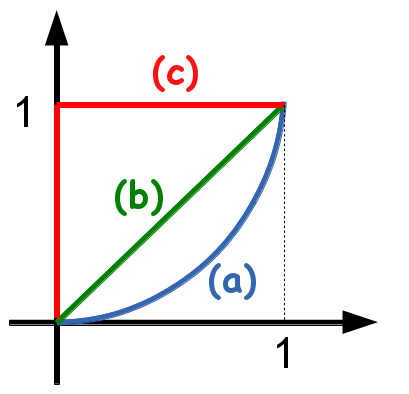
Seja $\mathbf{F}(x,y)=y^{2}\,\mathbf{i}+2xy\,\mathbf{j}$. Avalie a integral de linha de $\left(0,\,0\right)$ até $\left(1,\,1\right)$ seguindo

1. A linha reta $y=x$
2. A curva $y=x^{2}$
3. A curva suave definida por partes que consiste dos segmentos de reta que vão desde $\left(0,\,0\right)$ até $\left(0,\,1\right)$ e desde $\left(0,\,1\right)$ até $\left(1,\,1\right)$

Demonstre que o campo é um campo gradiente e determine o campo potencial.

SOL.

Seguindo o caminho (1): \[ \begin{align*} \mathbf{r}(t)= & t\,\mathbf{i}+t\,\mathbf{j}\\ \mathbf{v}(t)= & \mathbf{i}+\mathbf{j} \end{align*} \] onde $0\leq t\leq1$, dessa forma a \[ \begin{align*} \mathbf{F}\cdot d\mathbf{r}= & \left(y^{2}\,\mathbf{i}+2xy\,\mathbf{j}\right)\cdot\left(\mathbf{i}+\mathbf{j}\right)\\ = & \left(t^{2}\,\mathbf{i}+2t^{2}\,\mathbf{j}\right)\cdot\left(\mathbf{i}+\mathbf{j}\right)\\ = & t^{2}+2t^{2}\\ = & 3t^{2} \end{align*} \] dessa forma \[ \begin{align*} \int_{c}\mathbf{F}\cdot d\mathbf{r}= & 3\int_{0}^{1}t^{2}dt\\ = & \dfrac{3}{3}\left.t^{3}\right|_{0}^{1}\\ = & 1 \end{align*} \] Seguindo o caminho (1): \[ \begin{align*} \mathbf{r}(t)= & t\,\mathbf{i}+t^{2}\,\mathbf{j}\\ \mathbf{v}(t)= & \mathbf{i}+2t\,\mathbf{j} \end{align*} \] onde $0\leq t\leq1$, dessa forma a \[ \begin{align*} \mathbf{F}\cdot d\mathbf{r}= & \left(y^{2}\,\mathbf{i}+2xy\,\mathbf{j}\right)\cdot\left(\mathbf{i}+2t\,\mathbf{j}\right)\\ = & \left(t^{4}\,\mathbf{i}+2t^{3}\,\mathbf{j}\right)\cdot\left(\mathbf{i}+2t\,\mathbf{j}\right)\\ = & t^{4}+4t^{4}\\ = & 5t^{4} \end{align*} \] dessa forma \[ \begin{align*} \int_{c}\mathbf{F}\cdot d\mathbf{r}= & 5\int_{0}^{1}t^{4}dt\\ = & \dfrac{5}{5}\left.t^{5}\right|_{0}^{1}\\ = & 1 \end{align*} \] Seguindo o caminho (3): Neste caso devemos dividir a integral \[ \int_{c3}\mathbf{F}\cdot d\mathbf{r}=\int_{c3_{a}}\mathbf{F}\cdot d\mathbf{r}+\int_{c3_{b}}\mathbf{F}\cdot d\mathbf{r} \nonumber \] Seguindo o caminho (3a): \[ \begin{align*} \mathbf{r}(t)= & \left(0,\,0\right)+\left[\left(0,\,1\right)-\left(0,\,0\right)\right]t\\ = & t\,\mathbf{j}\\ \mathbf{v}(t)= & \mathbf{j} \end{align*} \] onde $0\leq t\leq1$, dessa forma a \[ \begin{align*} \mathbf{F}\cdot d\mathbf{r}= & \left(y^{2}\,\mathbf{i}+2xy\,\mathbf{j}\right)\cdot\left(\mathbf{j}\right)\\ = & \left(t^{2}\,\mathbf{i}\right)\cdot\left(\mathbf{j}\right)\\ = & 0 \end{align*} \] dessa forma \[ \begin{align*} \int_{c3_{a}}\mathbf{F}\cdot d\mathbf{r}= & \int_{0}^{1}0\, dt\\ = & 0 \end{align*} \] Seguindo o caminho (3b): \[ \begin{align*} \mathbf{r}(t)= & \left(0,\,1\right)+\left[\left(1,\,1\right)-\left(0,\,1\right)\right]t\\ = & t\,\mathbf{i}+\,\mathbf{j}\\ \mathbf{v}(t)= & \mathbf{i} \end{align*} \] onde $0\leq t\leq1$, dessa forma a \[ \begin{align*} \mathbf{F}\cdot d\mathbf{r}= & \left(y^{2}\,\mathbf{i}+2xy\,\mathbf{j}\right)\cdot\left(\mathbf{i}\right)\\ = & \left(\mathbf{i}+2t\,\mathbf{j}\right)\cdot\left(\mathbf{i}\right)\\ = & 1 \end{align*} \] dessa forma \[ \begin{align*} \int_{c3_{b}}\mathbf{F}\cdot d\mathbf{r}= & \int_{0}^{1}dt\\ = & \left.t\right|_{0}^{1}\\ = & 1 \end{align*} \] por tanto, \[ \begin{align*} \int_{c3}\mathbf{F}\cdot d\mathbf{r}= & \int_{c3_{a}}\mathbf{F}\cdot d\mathbf{r}+\int_{c3_{b}}\mathbf{F}\cdot d\mathbf{r}\\ = & 0+1\\ = & 1 \end{align*} \]

Observe que todas as soluções deram o mesmo resultado, por tanto a integral ser independente do caminho escolhido. Isso é um indicativo de que o campo é um campo gradiente, verificando \[ \begin{align*} \vec{\nabla}\times\mathbf{F}= & \begin{bmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial\;}{\partial x} & \dfrac{\partial\;}{\partial y} & \dfrac{\partial\;}{\partial z}\\ y^{2} & 2xy & 0 \end{bmatrix}\\ = & \left(0-0\right)\;\mathbf{i}-\left(0-0\right)\;\mathbf{j}+\left(2y-2y\right)\;\mathbf{k}\\ = & \mathbf{0} \end{align*} \] assim \[ \begin{align*} \mathbf{F}= & \vec{\nabla}f\\ F_{x}\,\mathbf{i}+F_{y}\,\mathbf{j}+F_{z}\,\mathbf{k}= & \dfrac{\partial f}{\partial x}\,\mathbf{i}+\dfrac{\partial f}{\partial y}\,\mathbf{j}+\dfrac{\partial f}{\partial z}\,\mathbf{k}\\ F_{x}= & \dfrac{\partial f}{\partial x}\\ F_{y}= & \dfrac{\partial f}{\partial y}\\ F_{z}= & \dfrac{\partial f}{\partial z} \end{align*} \] dessa forma \[ \begin{align*} \dfrac{\partial f}{\partial x}= & y^{2}\\ f= & \int y^{2}dx\\ = & xy^{2}+C_{1}\left(y,\, z\right) \end{align*} \] derivando \[ \begin{align*} \dfrac{\partial\,}{\partial y}\left(xy^{2}+C_{1}\left(y,\, z\right)\right)= & F_{y}\\ 2xy+\dfrac{\partial C_{1}}{\partial y}= & 2xy\\ C_{1}= & \int0\, dy\\ = & C_{2}\left(z\right) \end{align*} \] dessa forma \[ f=xy^{2}+C_{1}\left(z\right) \nonumber \] que, derivando \[ \begin{align*} \dfrac{\partial\,}{\partial z}\left(xy^{2}+C_{2}\left(z\right)\right)= & F_{z}\\ \dfrac{\partial C_{2}}{\partial z}= & 0\\ C_{2}= & const \end{align*} \] por tanto \[ f=xy^{2}+C \nonumber \] Como \[ D\left[\mathbf{F}\right]=\mathbb{R}\Rightarrow\text{domínio conexo} \nonumber \] dessa forma \[ \begin{align*} \int_{c}\mathbf{F}\cdot d\mathbf{r}= & f(B)-f(A)\\ = & f(1,\,1)-f(0,\,0)\\ = & 1-0\\ = & 1 \end{align*} \]

Exemplo 07

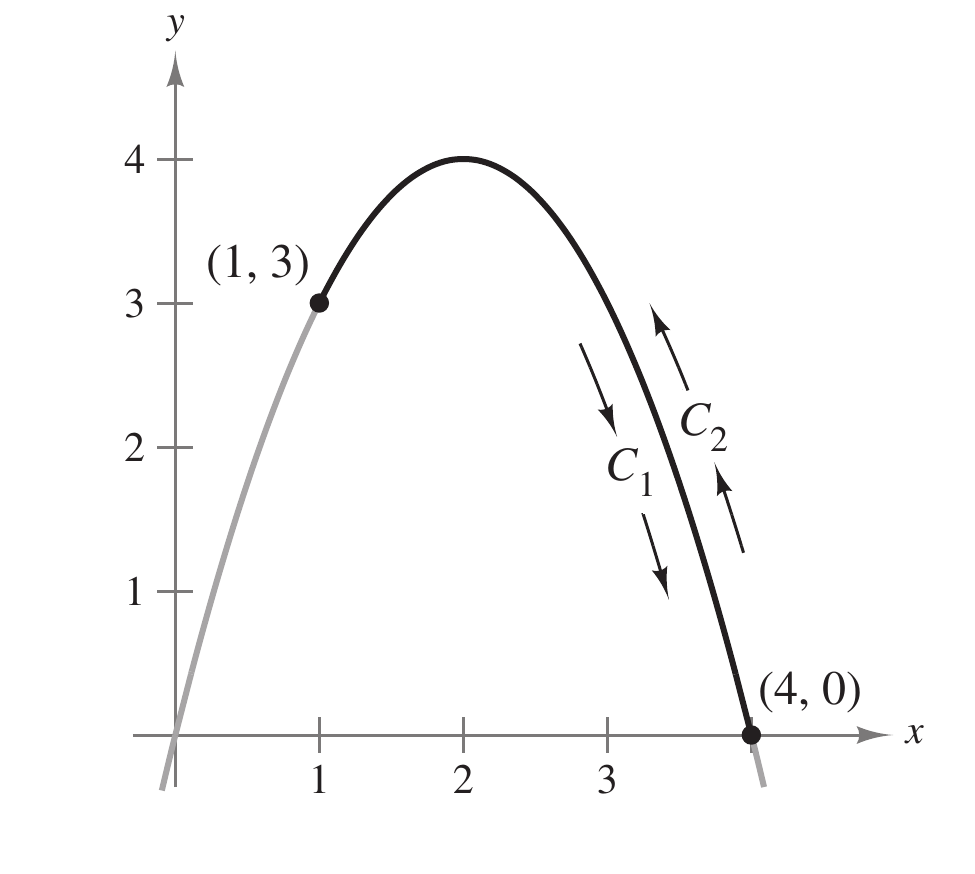
Avaliar a integral \[ \int_{C}y\, dx+x^{2}dy \nonumber \] onde $C$ é o arco parabólico dado por $y=4x-x^{2}$ desde $(1,\,3)$ até $(4,\,0)$, como se mostra na figura. Seguidamente calcule a mesma integral mas agora seguindo o caminho da curva com orientação oposta a descrita pela equação anterior.

SOL.

Primeiro calculamos para o caso da curva com orientação positiva: \[ \begin{align*} \mathbf{r}(t)= & t\,\mathbf{i}+\left(4t-t^{2}\right)\,\mathbf{j}\\ \mathbf{v}(t)= & \mathbf{i}+\left(4-2t\right)\,\mathbf{j} \end{align*} \] então \[ \begin{align*} \int_{C}y\, dx+x^{2}dy= & \int_{1}^{4}\left(4t-t^{2}\right)dt+\int_{1}^{4}t^{2}\left(4-2t\right)dt\\ = & \int_{1}^{4}\left(4t+3t^{2}-2t^{3}\right)dt\\ = & \left[2t^{2}+t^{3}-\dfrac{1}{2}t^{4}\right]_{1}^{4}\\ = & \left(32+64-128\right)-\left(2+1-\dfrac{1}{2}\right)\\ = & -\dfrac{69}{2} \end{align*} \] Para o caso da curva com orientação oposta: \[ \begin{align*} \mathbf{r}^{-}(t)= & \mathbf{r}(1+4-t)\\ = & \left(5-t\right)\,\mathbf{i}+\left[4\left(5-t\right)-\left(5-t\right)^{2}\right]\,\mathbf{j}\\ = & \left(5-t\right)\,\mathbf{i}+\left[\left(5-t\right)\left(4-5+t\right)\right]\,\mathbf{j}\\ = & \left(5-t\right)\,\mathbf{i}+\left(5-t\right)\left(t-1\right)\,\mathbf{j}\\ = & \left(5-t\right)\,\mathbf{i}+\left(5t-5-t^{2}+t\right)\,\mathbf{j}\\ = & \left(5-t\right)\,\mathbf{i}+\left(-5+6t-t^{2}\right)\,\mathbf{j}\\ \mathbf{v}^{-}(t)= & -\mathbf{i}+\left(6-2t\right)\,\mathbf{j} \end{align*} \] de forma que \[ \begin{align*} \int_{C}y\, dx+x^{2}dy= & -\int_{1}^{4}\left(-5+6t-t^{2}\right)dt+\int_{1}^{4}\left(5-t\right)^{2}\left(6-2t\right)dt\\ = & -\int_{1}^{4}\left(-5+6t-t^{2}\right)dt+\int_{1}^{4}\left(25-10t+t^{2}\right)\left(6-2t\right)dt\\ = & -\int_{1}^{4}\left(-5+6t-t^{2}\right)dt+\int_{1}^{4}\left(150-60t+6t^{2}-50t+20t^{2}-2t^{3}\right)dt\\ = & \int_{1}^{4}\left(5-6t+t^{2}\right)dt+\int_{1}^{4}\left(150-110t+26t^{2}-2t^{3}\right)dt\\ = & \int_{1}^{4}\left(155-116t+27t^{2}-2t^{3}\right)dt\\ = & \left[155t-58t^{2}+9t^{3}-\dfrac{1}{2}t^{4}\right]_{1}^{4}\\ = & \left(620-928+576-128\right)-\left(155-58+9-\dfrac{1}{2}\right)\\ = & \dfrac{69}{2} \end{align*} \]

Exemplo 08

Calcular o trabalho realizado ao mover uma partícula desde $P_{1}=\left(0,\,0,\,0\right)$ até $P_{2}=\left(4,\,8,\,1\right)$ ao longo do caminho \[ \mathbf{r}(t)=\left(t^{2},\, t^{3},\, t\right)\quad\text{(em metros)}\qquad\qquad\text{para }1\leq t\leq2 \nonumber \] na presencia da força $\mathbf{F}(t)=\left(x^{2},\,-z,\,-\dfrac{y}{z}\right)$, dada em newtons.

SOL.

Escrevendo a força em termos da posição \[ \begin{align*} \mathbf{F}(\mathbf{r})= & \mathbf{F}\left(t^{2},\, t^{3},\, t\right)\\ = & \left(t^{4}\,-t,\,-t^{2}\right) \end{align*} \] agora calculando a velocidade \[ \mathbf{v}(t)=\left(2t,\,3t^{2},\,1\right) \nonumber \] de forma que \[ \begin{align*} \mathbf{F}\cdot\mathbf{v}= & \left(t^{4}\,-t,\,-t^{2}\right)\cdot\left(2t,\,3t^{2},\,1\right)\\ = & 2t^{5}-3t^{3}-t^{2} \end{align*} \] assim \[ \begin{align*} W= & \int_{C}\mathbf{F}\cdot d\mathbf{r}\\ = & \int_{C}\mathbf{F}\cdot\mathbf{v}\, dt\\ = & \int_{1}^{2}\left(2t^{5}-3t^{3}-t^{2}\right)\, dt\\ = & \left[\dfrac{1}{3}t^{6}-\dfrac{3}{4}t^{4}-\dfrac{1}{3}t^{3}\right]_{1}^{2}\\ = & \left(\dfrac{64}{3}-12-\dfrac{8}{3}\right)-\left(\dfrac{1}{3}-\dfrac{3}{4}-\dfrac{1}{3}\right)\\ = & \dfrac{20}{3}-\dfrac{3}{4}\\ = & -\dfrac{89}{12} \end{align*} \]

Exemplo 09

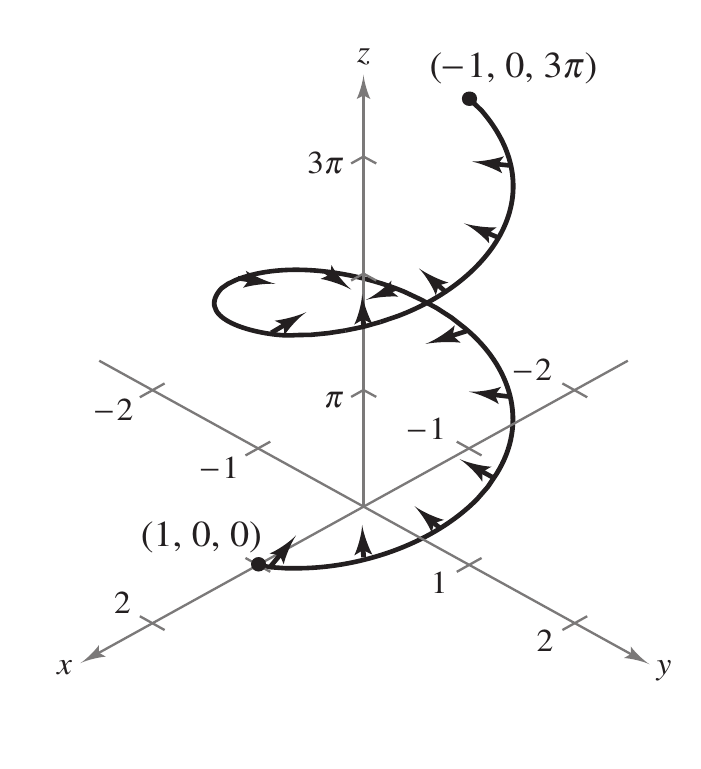
Encontre o trabalho feito pelo campo de força \[ \mathbf{F}(x,y,z)=-\dfrac{1}{2}x\,\mathbf{i}-\dfrac{1}{2}y\,\mathbf{j}+\dfrac{1}{4}\,\mathbf{k} \nonumber \] onde as partículas se movem ao longo da hélice dado por \[ \mathbf{r}(t)=\cos t\,\mathbf{i}+\sin t\,\mathbf{j}+t\,\mathbf{k} \nonumber \] desde o ponto $\left(1,\,0,\,0\right)$ até $\left(-1,\,0,\,3\pi\right)$, como se mostra na figura.

SOL.

Escrevendo a força em termo da posição \[ \mathbf{F}(\mathbf{r}(t))=-\dfrac{1}{2}\cos t\,\mathbf{i}-\dfrac{1}{2}\sin t\,\mathbf{j}+\dfrac{1}{4}\,\mathbf{k} \nonumber \] escrevendo a velocidade \[ \mathbf{v}(t)=-\sin t\,\mathbf{i}+\cos t\,\mathbf{j}+\mathbf{k} \nonumber \] Considerando que os pontos entre os que será feita a integração são de $\left(1,\,0,\,0\right)$ até $\left(-1,\,0,\,3\pi\right)$ o que representa $t=0$ até $t=3\pi$, temos que a integral será \[ \begin{align*} W= & \int_{c}\mathbf{F}\cdot d\mathbf{r}\\ = & \int_{0}^{3\pi}\left(-\dfrac{1}{2}\cos t\,\mathbf{i}-\dfrac{1}{2}\sin t\,\mathbf{j}+\dfrac{1}{4}\,\mathbf{k}\right)\cdot\left(-\sin t\,\mathbf{i}+\cos t\,\mathbf{j}+\mathbf{k}\right)dt\\ = & \int_{0}^{3\pi}\left(\dfrac{1}{2}\sin t\cos t-\dfrac{1}{2}\sin t\cos t+\dfrac{1}{4}\right)dt\\ = & \dfrac{1}{4}\int_{0}^{3\pi}dt\\ = & \dfrac{3\pi}{4} \end{align*} \]

Exemplo 10

Calcule a integral o trabalho realizado pela força $\mathbf{F}(x,y)=-y\,\mathbf{i}+x\,\mathbf{j}$ ao longo das curvas $x^{2}+y^{2}=9$ (para $x,\, y$ no I quadrante) e $\mathbf{r}(t)=t\,\mathbf{i}+2t\,\mathbf{j}$ (neste caso $0\leq t\leq1$).

SOL.

Para o caso do I caminho observamos que uma parametrização adequada é \[ \mathbf{r}(t)=3\cos t\,\mathbf{i}+3\sin t\,\mathbf{j},\qquad0\leq t\leq\dfrac{\pi}{2} \nonumber \] de onde a velocidade está dada por \[ \mathbf{v}(t)=-3\sin t\,\mathbf{i}+3\cos t\,\mathbf{j} \nonumber \] nessa situação \[ \mathbf{F}(\mathbf{r}(t))=-\sin t\,\mathbf{i}+\cos t\,\mathbf{j} \nonumber \] note que a velocidade e a força são vetores paralelos \[ \mathbf{v}(t)=3\mathbf{F}(\mathbf{r}(t)) \nonumber \] A integral de linha \[ \begin{align*} W= & \int_{c}\mathbf{F}\cdot d\mathbf{r}\\ = & \int_{0}^{\frac{\pi}{2}}\left(-\sin t\,\mathbf{i}+\cos t\,\mathbf{j}\right)\cdot\left(-3\sin t\,\mathbf{i}+3\cos t\,\mathbf{j}\right)dt\\ = & 3\int_{0}^{\frac{\pi}{2}}dt\\ = & \dfrac{3\pi}{2} \end{align*} \] Para o caso do outro caminho \[ \mathbf{F}(\mathbf{r}(t))=-2t\,\mathbf{i}+t\,\mathbf{j} \nonumber \] enquanto a velocidade está dada por \[ \mathbf{v}(t)=\mathbf{i}+2\,\mathbf{j} \nonumber \] de onde \[ \begin{align*} W= & \int_{c}\mathbf{F}\cdot d\mathbf{r}\\ = & \int_{0}^{1}\left(-2t\,\mathbf{i}+t\,\mathbf{j}\right)\cdot\left(\mathbf{i}+2\,\mathbf{j}\right)dt\\ = & \int_{0}^{1}\left(-2t+2t\right)dt\\ = & 0 \end{align*} \] o que implica que o campo de forças é perpendicular à direção do movimento, como mostra a figura

Exemplo 11

Seja $\mathbf{F}(x,y,z)=\left(2xy+z,\, x^{2},\, x\right)$,

1. Verifique que a função $V(x,\, y,z)=x^{2}y+xz$ é uma função potencial do campo
2. Avalie $\int_{c}\mathbf{F}\cdot d\mathbf{r}$, onde $\mathbf{r}$ é o caminho $P=\left(1,\,-1,2\right)$ até $Q=\left(2,\,2,\,3\right)$

SOL.

Calculando o gradiente do campo escalar \[ \begin{align*} \vec{\nabla}V= & \dfrac{\partial V}{\partial x}\,\mathbf{i}+\dfrac{\partial V}{\partial y}\,\mathbf{j}+\dfrac{\partial V}{\partial z}\,\mathbf{k}\\ = & \left(2y+z\right)\,\mathbf{i}+x^{2}\,\mathbf{j}+x\,\mathbf{k} \end{align*} \] que exatamente igual ao campo $\mathbf{F}(x,y,z)$, assim \[ \begin{align*} \int_{c}\mathbf{F}\cdot d\mathbf{r}= & V(Q)-V(P)\\ = & \left[2^{2}(2)+(3)(2)\right]-\left[1^{2}*(-1)+(1)(2)\right]\\ = & 13 \end{align*} \]

Exemplo 12

Mostre que \[ \mathbf{F}=\left\langle 2xy+y^{3},\, x^{2}+3xy^{2}+2y\right\rangle \nonumber \] é um campo conservativo e encontre a função potencial.

SOL.

Primeiro calculamos as derivadas cruzadas a fim de testar se elas são iguais \[ \begin{align*} \dfrac{\partial F_{x}}{\partial y}= & \dfrac{\partial\,}{\partial y}\left(2xy+y^{3}\right)\\ = & 2x+3y^{2}\\ \dfrac{\partial F_{y}}{\partial x}= & \dfrac{\partial\,}{\partial x}\left(x^{2}+3xy^{2}+2y\right)\\ = & 2x+3y^{2} \end{align*} \] Isto, junto ao fato de que $D\left[\mathbf{F}\right]=\mathbb{R}^{2}$, o qual é um simplesmente conexo, nos permite afirmar que o campo define um campo conservativo. A função potencial associada a esse campo conservativo é \[ \begin{align*} \dfrac{\partial f}{\partial x}= & F_{x}\\ f= & \int\left(2xy+y^{3}\right)\, dx\\ = & x^{2}y+xy^{3}+C_{1}(y) \end{align*} \] derivando em relação a $y$ \[ \begin{align*} F_{y}= & \dfrac{\partial f}{\partial y}\\ x^{2}+3xy^{2}+2y= & \dfrac{\partial\,}{\partial y}\left(x^{2}y+xy^{3}+C_{1}(y)\right)\\ x^{2}+3xy^{2}+2y= & x^{2}+3xy^{2}+\dfrac{\partial C_{1}}{\partial y}\\ 2y= & \dfrac{\partial C_{1}}{\partial y}\\ C_{1}= & 2\int y\, dy\\ = & y+C \end{align*} \] por tanto \[ f=x^{2}y+xy^{3}+y+C \nonumber \]

Exemplo 13

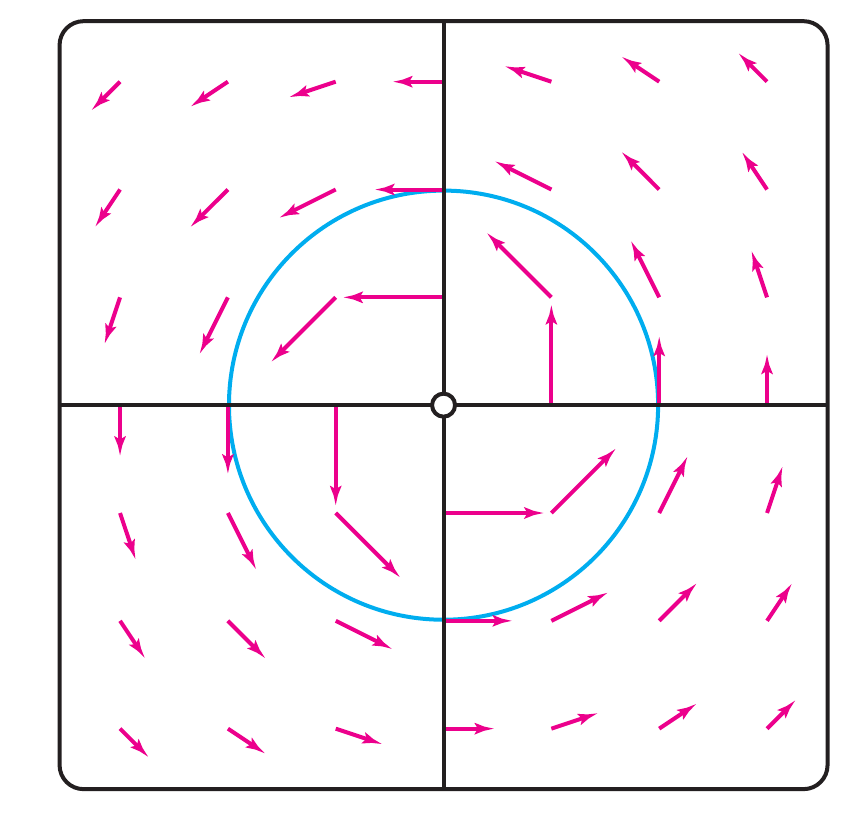
Mostre que o campo ciclone \[ \mathbf{F}=\left\langle -\dfrac{y}{x^{2}+y^{2}},\,\dfrac{x}{x^{2}+y^{2}}\right\rangle \nonumber \] é um campo irrotacional porem não é um campo conservativo.

SOL.

Antes de inciar devemos dizer que este campo corresponde ao campo magnético (indução magnética) produzido por um corrente elétrica que "flui" num fio reto infinito, calculada mediante a lei de Biot-Savart. Para ser um campo irrotacional as derivadas parciais cruzadas devem ser iguis \[ \begin{align*} \dfrac{\partial F_{x}}{\partial y}= & \dfrac{\partial\,}{\partial y}\left(-\dfrac{y}{x^{2}+y^{2}}\right)\\ = & \dfrac{-\left(x^{2}+y^{2}\right)+y\dfrac{\partial\,}{\partial y}\left(x^{2}+y^{2}\right)}{\left(x^{2}+y^{2}\right)^{2}}\\ = & \dfrac{y^{2}-x^{2}}{x^{2}+y^{2}}\\ \dfrac{\partial F_{y}}{\partial x}= & \dfrac{\partial\,}{\partial x}\left(\dfrac{x}{x^{2}+y^{2}}\right)\\ = & \dfrac{\left(x^{2}+y^{2}\right)-x\dfrac{\partial\,}{\partial y}\left(x^{2}+y^{2}\right)}{\left(x^{2}+y^{2}\right)^{2}}\\ = & \dfrac{y^{2}-x^{2}}{x^{2}+y^{2}} \end{align*} \] Agora vamos considerar um circuito fechado arbitraria, por simplicidade escolhemos \[ \begin{align*} \mathbf{r}(t)= & \cos t\,\mathbf{i}+\sin t\,\mathbf{j},\qquad0\leq t\leq2\pi\\ \mathbf{v}(t)= & -\sin t\,\mathbf{i}+\cos t\,\mathbf{j} \end{align*} \] a partir desta escolha podemos escrever \[ \mathbf{F}(\mathbf{r})=-\sin t\,\mathbf{i}+\cos t\,\mathbf{j} \nonumber \] de forma que \[ \begin{align*} \oint_{c}\mathbf{F}\cdot d\mathbf{r}= & \int_{0}^{2\pi}\mathbf{F}(\mathbf{r})\cdot\mathbf{v}\, dt\\ = & \int_{0}^{2\pi}dt\\ = & 2\pi \end{align*} \] o que corrobora o fato de que mesmo que o rotacional seja nulo o campo não é conservativo porque o domínio não é simplesmente conexo. Em teoria está integral deve ser zero se for escolhido um caminho tal que não contivesse o zero, desafortunadamente isto não pode ser provado para um domínio arbitrário (tipo no I quadrante). A única demonstração que temos é para um domínio definido por \[ R=\left\{ \left(x,\, y\right)|x\in\mathbb{R},\, y\in\left(0,\,\infty\right)\right\} \nonumber \]

O caminho de integração é o dado pela figura acima e está definido por: \[ \begin{align*} C_{1}:\,\mathbf{r}_{1}(t)= & t\,\mathbf{i},\qquad1\leq t\leq2\\ C_{2}:\,\mathbf{r}_{2}(t)= & 2\cos t\,\mathbf{i}+2\sin t\,\mathbf{j},\qquad0\leq t\leq\pi\\ C_{3}:\,\mathbf{r}_{3}(t)= & t\,\mathbf{i},\qquad-2\leq t\leq-1\\ C_{4}:\,\mathbf{r}_{4}(t)= & \cos t\,\mathbf{i}+\sin t\,\mathbf{j},\qquad\pi\leq t\leq0 \end{align*} \] dessa forma temos \[ \oint_{c}\mathbf{F}\cdot d\mathbf{r}=\int_{C_{1}}\mathbf{F}\cdot d\mathbf{r}+\int_{C_{2}}\mathbf{F}\cdot d\mathbf{r}+\int_{C_{3}}\mathbf{F}\cdot d\mathbf{r}+\int_{C_{4}}\mathbf{F}\cdot d\mathbf{r} \nonumber \] assim, para o caminho $C_{1}$: \[ \mathbf{F}=\left\langle -\dfrac{y}{x^{2}+y^{2}},\,\dfrac{x}{x^{2}+y^{2}}\right\rangle \nonumber \] \[ \begin{align*} \mathbf{v}_{1}= & \mathbf{i}\\ \mathbf{F}\left(\mathbf{r}_{1}\right)= & \dfrac{\mathbf{i}}{t} \end{align*} \] \[ \begin{align*} \int_{C_{1}}\mathbf{F}\cdot d\mathbf{r}= & \int_{1}^{2}\left(\dfrac{\mathbf{j}}{t}\right)\cdot\mathbf{i}\\ = & 0 \end{align*} \] para o caminho $C_{3}$: \[ \begin{align*} \mathbf{v}_{1}= & \mathbf{i}\\ \mathbf{F}\left(\mathbf{r}_{1}\right)= & \dfrac{\mathbf{i}}{t} \end{align*} \] \[ \begin{align*} \int_{C_{1}}\mathbf{F}\cdot d\mathbf{r}= & \int_{-2}^{-1}\left(\dfrac{\mathbf{j}}{t}\right)\cdot\mathbf{i}\\ = & 0 \end{align*} \] para o caminho $C_{2}$: \[ \begin{align*} \mathbf{v}_{2}= & -2\sin t\,\mathbf{i}+2\cos t\,\mathbf{j}\\ \mathbf{F}\left(\mathbf{r}_{2}\right)= & -\dfrac{1}{2}\sin t\,\mathbf{i}+\dfrac{1}{2}\cos t\,\mathbf{j} \end{align*} \] \[ \begin{align*} \int_{C_{1}}\mathbf{F}\cdot d\mathbf{r}= & \int_{0}^{\pi}\left(-\dfrac{1}{2}\sin t\,\mathbf{i}+\dfrac{1}{2}\cos t\,\mathbf{j}\right)\cdot\left(-2\sin t\,\mathbf{i}+2\cos t\,\mathbf{j}\right)dt\\ = & \int_{0}^{\pi}\left(\sin^{2}t+\cos^{2}t\right)dt\\ = & \pi \end{align*} \] para o caminho $C_{4}$: \[ \begin{align*} \mathbf{v}_{4}= & -\sin t\,\mathbf{i}+\cos t\,\mathbf{j}\\ \mathbf{F}\left(\mathbf{r}_{4}\right)= & -\sin t\,\mathbf{i}+\cos t\,\mathbf{j} \end{align*} \] \[ \begin{align*} \int_{C_{1}}\mathbf{F}\cdot d\mathbf{r}= & \int_{\pi}^{0}\left(-\sin t\,\mathbf{i}+\cos t\,\mathbf{j}\right)\cdot\left(-\sin t\,\mathbf{i}+\cos t\,\mathbf{j}\right)dt\\ = & \int_{\pi}^{0}\left(\sin^{2}t+\cos^{2}t\right)dt\\ = & -\pi \end{align*} \] finalmente \[ \oint_{c}\mathbf{F}\cdot d\mathbf{r}=0+\pi-\pi+0=0 \nonumber \] A função potencial associada é: \[ \begin{align*} \dfrac{\partial f}{\partial x}= & -\dfrac{y}{y^{2}+x^{2}}\\ = & \int\left(-\dfrac{y}{y^{2}+x^{2}}\right)dx\\ = & -\arctan\dfrac{x}{y}+C\\ \dfrac{\partial f}{\partial y}= & \dfrac{\partial\,}{\partial y}\left(-\arctan\dfrac{x}{y}+C_{1}\right)\\ \dfrac{x}{y^{2}+x^{2}}= & -\dfrac{\dfrac{d\,}{dy}\left(\dfrac{x}{y}\right)}{1+\left(\dfrac{x}{y}\right)^{2}}+\dfrac{\partial C_{1}}{\partial y}\\ = & \dfrac{\left(\dfrac{x}{y^{2}}\right)}{1+\left(\dfrac{x}{y}\right)^{2}}+\dfrac{\partial C_{1}}{\partial y}\\ = & \dfrac{x}{y^{2}+x^{2}}+\dfrac{\partial C_{1}}{\partial y}\\ \dfrac{\partial C_{1}}{\partial y}= & Const. \end{align*} \] por tanto \[ f=-\arctan\dfrac{x}{y}+C \nonumber \]

Exemplo 14

Seja \[ \mathbf{F}(x,y)=\left\langle y,\, x\right\rangle \nonumber \] um campo vetorial conservativo, calcule a função potencial do qual deriva utilizando o método da integral

SOL.

O método da integral consiste em admitir a independência da integral de linha do caminho de integração, dessa forma se \[ \mathbf{F}(x,y)=\vec{\nabla}f \nonumber \] temos \[ \int_{c}\mathbf{F}\cdot d\mathbf{r}=f(x,y)-f(A) \nonumber \] vamos supor que o ponto inicial é \[ f(A)=f(0,0)=C \nonumber \] de onde \[ F(x,\, y)=\int_{c}\mathbf{F}\cdot d\mathbf{r}+C \nonumber \] Para resolver essa integral vamos considerar uma reta que se estende desde o ponto $A=(0,0)$ até o ponto $B=(x,y)$, assim nosso caminho terá a seguinte equação \[ \begin{align*} \mathbf{r}(t)= & xt\,\mathbf{i}+yt\,\mathbf{j},\qquad0\leq t\leq1\\ \mathbf{v}(t)= & x\,\mathbf{i}+y\,\mathbf{j}\\ \mathbf{F}(\mathbf{r})= & yt\,\mathbf{i}+xt\,\mathbf{j}\\ \mathbf{F}\cdot\mathbf{v}= & 2xyt \end{align*} \] de onde \[ \int_{c}\mathbf{F}\cdot d\mathbf{r}=2\int_{0}^{1}xyt\, dt=xy \nonumber \] assim \[ F(x,\, y)=xy+C \nonumber \]