Exemplo 01

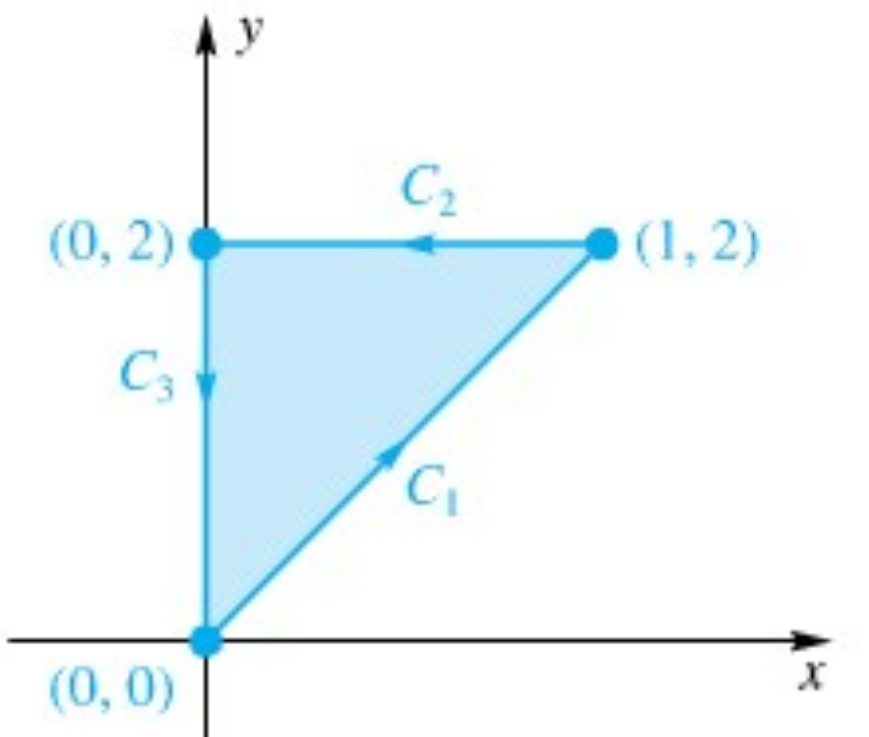
Seja $C$ a fronteira do triangulo com vértice $(0,0)$, $(1,2)$ e $(0,2)$, avalie a integral \[ \oint_C 4x^2ydx + 2ydy \nonumber \] utilizando o método direto e pelo teorema de Green.
SOL.
Como podemos ver na figura o caminho de integral é formado por 3 caminhos diferentes, $C_1: y = 2x$, $C_2: y=2$, $C_3: x=0$, \[ \begin{align*} \int_{C_1} 4x^2ydx+2ydy &= \int_0^1 4x^2(2x) + 2(2x)(2dx)\\ &= \int_0^1 \left( 8x^3+8x \right)dx\\ &= \left[ 2x^4+4x^2 \right]_0^1\\ &= 6\\ \int_{C_2} 4x^2ydx+2ydy &=\int_1^0 4x^2(2)dx\\ & = 8\int_1^0x^2dx\\ & = -\dfrac{8}{3}\\ \int_{C_3} 4x^2ydx+2ydy &= \int_2^0 2ydy\\ & = -4 \end{align*} \] por tanto \[ \begin{align*} \oint_C 4x^2ydx + 2ydy & = 6 - \dfrac{8}{3} - 4\\ &= \dfrac{2}{3} \end{align*} \] Utilizando o teorema de Green \[ \begin{align*} \oint_C 4x^2ydx + 2ydy &= \int_R \left[ \dfrac{\partial \,}{\partial x} (2y)\dfrac{\partial \,}{\partial y}(4x^2y\right]dxdy\\ & = \int_0^1\int_{2x}^2 -4x^2dx\\ & = \int_0^1 \left( -8x^2 + 8x^3 \right)dx\\ & = \left[ -\dfrac{8}{3}x^3 + 2x^4\right]_0^1\\ & = -\dfrac{2}{3} \end{align*} \]

Exemplo 02

Verifique o teorema de Green para o caso da integral de linha \[ \oint_C xy^2dx+xdy \nonumber \] ao longo do círculo $C$, orientado em sentido anti horário.
SOL.
Primeiro vamos a calcular a integral de linha de forma direta, para isso vamos parametrizar o círculo mediante $\mathbf{r}(t) = \cos t\,\mathbf{i} + \sin t \,\mathbf{j}$, com $0\leq t \leq 2\pi$, a partir disto temos \[ \begin{array}{rclcrcl} x &=& \cos t &\;\;\;& y &=& \sin t\\ dx &=& -\sin t \,dt&\;\;\;& dy &=& \cos t \,dt \end{array} \nonumber \] assim \[ \oint_C xy^2dx+xdy = \int_0^{2\pi} -\cos t\sin^3 t\,dt + \cos^2 t dt \nonumber \] utilizando a substituição $u = \sin\,t\Rightarrow \cos \, t$ e $\cos^2 t = \frac{1}{2}\left( 1 \cos 2t \right)$, de onde \[ \begin{align*} \oint_C xy^2dx+xdy &= -\left. \dfrac{\sin^4}{4} t \right|_0^{2\pi} + \left. \dfrac{1}{2}\left( t + \dfrac{1}{2}\sin 2t \right) \right|_0^{2\pi}\\ & = 0 + \dfrac{1}{2}\left( 2\pi + 0 \right)\\ & = \pi \end{align*} \] Aplicando o teorema de green \[ \begin{align*} \oint_C xy^2dx+xdy &= \iint_R \left( \dfrac{\partial \,}{\partial x}(x) - \dfrac{\partial \,}{\partial y}(xy^2) \right)\,dxdy\\ & = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}\left( 1-2xy \right) dxdy\\ & = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} dxdy - \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} 2xy\,dxdy \end{align*} \] Passando para polares a I integral termos \[ \begin{align*} \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} dxdy &= \int_0^1\int_0^{2\pi}rd\theta dr\\ & = \pi \end{align*} \] no caso da segunda integral teremos \[ \begin{align*} \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} 2xy\,dxdy &= \int_{-1}^1\left. xy^2 \right|_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}dx\\ & = \int_{-1}^1 x\left[ \left( \sqrt{1-x^2} \right)^2 - \left( -\sqrt{1-x^2} \right)^2 \right]\\ & = 0 \end{align*} \] por tanto \[ \oint_C xy^2dx+xdy = \pi \nonumber \]

Exemplo 03

Utilize o teorema de Green para avaliar \[ \oint_C x^2y\,dx+x\,dy \nonumber \] ao longo do caminho mostrado na figura ao lado.
SOL.
Para este problema $M(x,y) = x^2y$ e $N(x,y)=x$, dessa forma \[ \begin{align*} \oint_C x^2y\,dx+x\,dx &= \iint_R \left[ \dfrac{\partial \,}{\partial x} \left( x \right) - \dfrac{\partial \,}{\partial y}\left( x^2y \right) \right] dxdy\\ &= \int_0^1\int_0^{2x} \left( 1 - x^2 \right)dydx\\ &= \int_0^1 \left( 2x - 2x^3 \right) dx\\ &= \left[ x^2 - \dfrac{x^4}{2} \right]_0^1\\ &= \dfrac{1}{2} \end{align*} \nonumber \]

Exemplo 04

Utilize o teorema de Green para avaliar a integral \[ \oint_C y^3dx + \left( x^3 + 3xy^2 \right)dy \nonumber \]
SOL.
Para este caso $M = y^3$ e $N = x^3+3xy^2$, de onde \[ \dfrac{\partial N}{\partial x}=3x^2+3y^2\;\;\;\;\;\;\;\;\dfrac{\partial M}{\partial y}= 3y^2 \nonumber \] Aplicando o teorema de Green \[ \begin{align*} \oint_C y^3dx + \left( x^3 + 3xy^2 \right)dy &= \iint_D \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y} \right)\,dxdy\\ & = \int_0^1\int_{x^3}^x \left[ \left( 3x^2 + 3y^3 \right) - 3y^2 \right]dydx\\ & = \int_0^1\int_{x^3}^x 3x^2 dydx\\ & = \int_0^1 \left. 3x^2y\right|_{x^3}^x dx\\ & = \int_0^1 \left( 3x^3 - 3x^5 \right) dx\\ & = \left. \dfrac{3x^4}{4} - \dfrac{x^6}{2}\right|_0^1\\ & = \dfrac{1}{4} \end{align*} \nonumber \]

Exemplo 05

Avalie a integral de linha de \[ \oint_C \left( 7y-e^{\sin x} \right)dx + \left[ y^3-\sin\left( y^3+8y \right) \right]dy, \nonumber \] onde $C$ é o círculo de raio $3$ centrado no ponto $(5,-7)$
SOL.
Este problema ilustra claramente a facilidade introduzida pelo teorema de Green, a integral de linha é virtualmente impossível de resolver, mas a partir do teorema de Green ela é bastante simples: \[ \begin{align*} \oint_C \left( 7y-e^{\sin x} \right)dx + \left[ y^3-\sin\left( y^3+8y \right) \right]dy &= \iint_R \left[ \dfrac{\partial \,}{\partial x}\left[ y^3-\sin\left( y^3+8y \right) \right] - \dfrac{\partial \,}{\partial y} \left(7y-e^{\sin x} \right)\right]\,dxdy\\ &= (15-7)dxdy\\ &= 8 \iint_R da\\ &= 72\pi \end{align*} \nonumber \]

Exemplo 06

Utilize o teorema de Green para avaliar a integral $\displaystyle \oint \left( x^2+y^2 \right)dx + 3xy^2dy$, onde $C$ consiste da porção de curva $y=x^2$ definido entr $(2,4)$ até $(0,0)$, seguido da reta que vai desde $(0,0)$ até $(2,0)$, e que finaliza com a reta que vai desde $(2,0)$ até (2,4)$
SOL.
Vemos que o trajeto definido pelo problema é uma curva suave seccionalmente suave, com orientação positiva, dessa forma o teorema de Green é aplicável, \[ \begin{align*} \oint_C \left( x^2+y^2 \right)dx + 3xy^2dy &= \iint_R \left[ \dfrac{\partial \,}{\partial x}\left( 3xy^2 \right) - \dfrac{\partial \,}{\partial y} \left( x^2+y^2 \right)\right]\,dxdy\\ &= \iint_R\left( 3y^2-3y^2 \right)dxdy\\ &= 0 \end{align*} \nonumber \] Dessa forma a integral de linha é zero. Vale aqui relembrar um fato relacionado com as integrais de linha, vimos que se $\displaystyle \oint \mathbf{F}\cdot d\mathbf{r} = 0$ e se o $D[\mathbf{F}$ é simplesmente conexo então o campo é dito conservativo. Para o caso deste problema em partícular o campo escalar do qual deriva o campo $\mathbf{F}$ é $f(x,y) = \frac{1}{3}x^3+xy^3$.

Exemplo 07

Uma partícula viaja uma vez ao redor do círculo de raio $3$ centrado na origem devido a ação da força \[ \mathbf{F}(t) =y^3 \,\mathbf{i} + \left( x^3 + 3xy^2 \right)\,\mathbf{j} \nonumber \] Determine o trabalho realizado pela força.
SOL.
Por definição \[ \begin{align*} W &= \int_C\mathbf{F}\cdot d\mathbf{r}\\ & \int_C y^3dx + \left( x^3 + 3xy^2 \right)dy \end{align*} \] aplicando o teorema de Green \[ \begin{align*} W &= \iint_R \left[ \dfrac{\partial \,}{\partial x}\left( x^3 + 3xy^2 \right) - \dfrac{\partial \,}{\partial y} \left( y^3 \right)\right]\,dxdy\\ & = \iint_R \left( 3x^2+3y^2-3y^2 \right) dxdy \end{align*} \] passando para polares \[ \begin{align*} W &= 3\int_0^{2\pi}\int_0^3r^3\cos^2\theta drd\theta\\ &= 3\int_0^{2\pi} \left[ \dfrac{r^4}{4} \cos^2 \theta \right]_0^3 d\theta\\ &= \dfrac{243}{8}\int_0^{2\pi} \left( 1+\cos 2\theta \right)d\theta\\ &= \dfrac{243}{8}\left[ \theta + \dfrac{sin^2\theta}{2} \right]\\ &= \dfrac{243\pi}{4} \end{align*} \]

Exemplo 08

Encontre a área encerrada pela elipse \[ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \nonumber \]
SOL.
Parametrizando a elipse temos \[ \begin{align*} x & = a \cos t\\ y & = b \sin t \end{align*} \] Observe que o lado direito do teorema de Green é \[ \iint_R \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y} \right)\,dxdy \nonumber \] onde $da = dxdy$, por tanto se $N=x$ e $M=-y$, essa integral será \[ 2\iint_R da = \oint xdy - ydx \nonumber \] utilizando \[ \begin{align*} dx & = -a \sin t\\ dy & = b \cos t \end{align*} \] temos \[ \begin{align*} \iint_R da& = \dfrac{1}{2}\oint \left[ \left( a \cos t \right)\left( b \cos t \right) - \left( b \sin t \right)\left( b \cos t \right) \right]dt\\ & = \dfrac{1}{2}\int_0^2\pi ab\left( \sin^2 t+\cos^2 t \right)dt\\ &= ab\pi \end{align*} \]

Exemplo 09

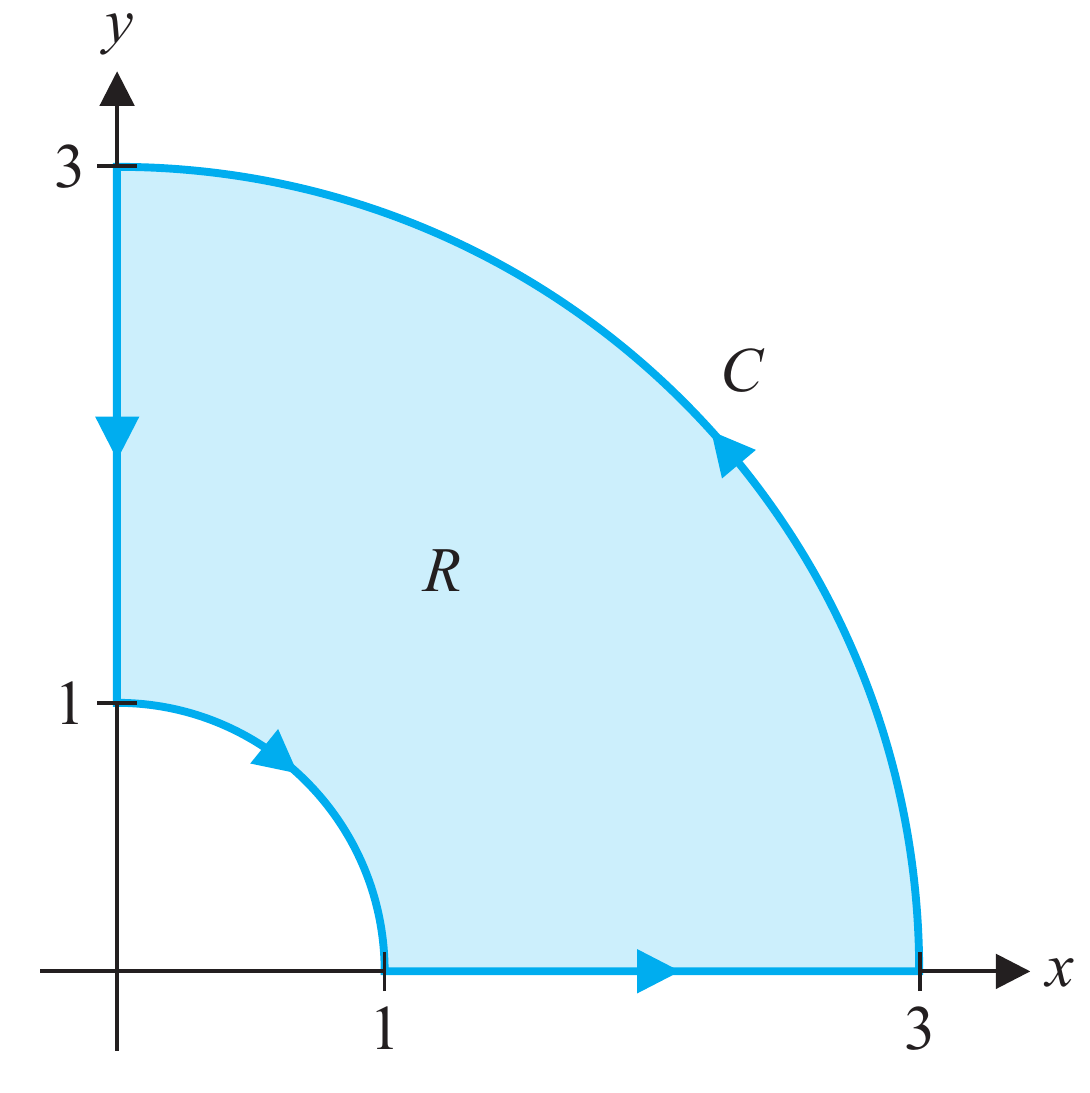
Avalie a integral \[ \oint_C \left( e^x + 6xy \right)dx + \left( 8x^2+ \sin y^2 \right)dy \nonumber \] onde $C$ é a curva positivamente orientada que delimita a região formada pelo anel de raio interno $1$ e raio externo $3$, definido no I quadrante.
SOL.
Aplicando o teorema \[ \begin{align*} \oint_C \left( e^x + 6xy \right)dx + \left( 8x^2+ \sin y^2 \right)dy &= \iint_R \left[ \dfrac{\partial \,}{\partial x}\left( 8x^2+ \sin y^2 \right) - \dfrac{\partial \,}{\partial y} \left( e^x + 6xy \right)\right]\,dxdy\\ & = \iint_R \left( 16x-6x \right) dxdy\\ & = \iint_R 10x \,dxdy \end{align*} \] utilizando coordenadas polares \[ \begin{align*} \oint_C \left( e^x + 6xy \right)dx + \left( 8x^2+ \sin y^2 \right)dy &= \int_0^{2\pi}\int_1^3 10r^2\cos \theta drd\theta\\ &= \int_0^{2\pi}\left[ \dfrac{10r^3}{3} \cos \theta\right]_1^3d\theta\\ &= \left.\dfrac{10}{3} \left( 3^3 - 1^3 \right)\sin \theta \right|_0^{2\pi}\\ &= \dfrac{260}{3} \end{align*} \]

Exemplo 10

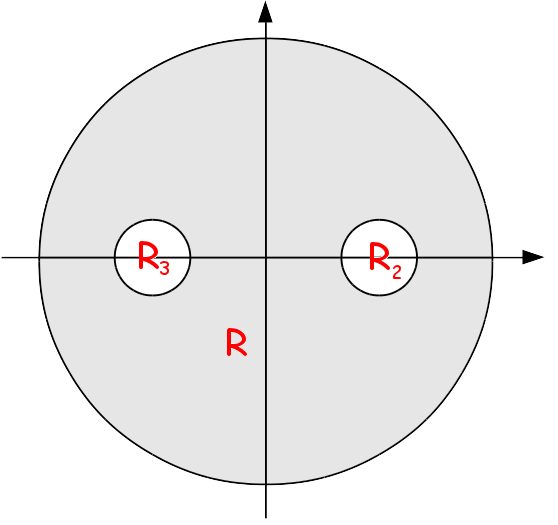
Considere as regiões \[ \begin{align*} R_1 &= \left\{ \left. \left( x,\,y \right) \right|\,x^2+y^2\leq 16 \right\}\\ R_2 &= \left\{ \left. \left( x,\,y \right) \right|\,\left( x-2 \right)^2 + y^2 \leq 1 \right\}\\ R_3 &= \left\{ \left. \left( x,\,y \right) \right|\,\left( x+2 \right)^2 + y^2 \leq 1\right\} \end{align*} \] Calcule o a integral \[ \oint_C \mathbf{F} \cdot d\mathbf{s} \nonumber \] para o caso em que o campo está dado por $\displaystyle \mathbf{F} = -y\,\mathbf{i} + x\,\mathbf{j}$, e $C$ delimita a região $R$, definida como $R = R_1 -\left( R_2\cup R_3\right)$, de forma direta e pelo teorema de green
SOL.
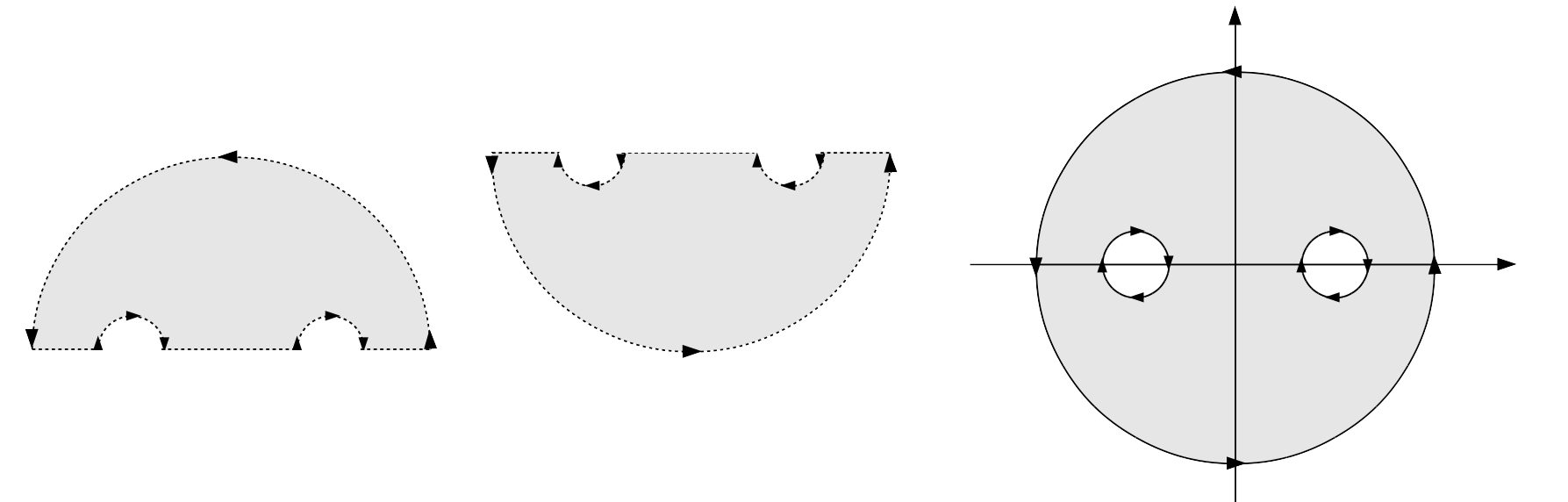
Neste problema devemos identificar cuidadosamente o trajeto de integração, para isso apresento abaixo a divisão feita e o resultado de sua união

Note que quando unimos as duas regiões obtemos a região mais a direita que coincide com nosso gráfico, perceba que a região delimitada, $S$, está definida pelas fronteiras $\delta R^+$, $\delta R_2^-$ e $\delta R_3^-$, onde o sinal positivo e negativo indicam caminhar no sentido anti horários e horário, respectivamente, dessa forma teremos \[ \oint_C \mathbf{F} \cdot d\mathbf{s} = \oint_{\delta R^+} \mathbf{F} \cdot d\mathbf{s} + \oint_{\delta R_2^-} \mathbf{F} \cdot d\mathbf{s} + \oint_{\delta R_3^-} \mathbf{F} \cdot d\mathbf{s} \nonumber \] onde, a parametrização para $\delta R^+$: \[ \begin{align*} x &= 4\cos t\\ dx & = -4\sin t\,dt\\ y &= 4\sin t\\ dy &= 4\cos t\,dt \end{align*} \] para $\delta R_2^-$, o vetor que define essa curva é \[ \mathbf{r}_2(t) = \left( 2+\cos t \right) \,\mathbf{i} + \sin t\,\mathbf{j} \nonumber \] mas como estamos olhando para a curva com orientação reversa \[ \begin{align*} \mathbf{r}^-_2(t)& =\mathbf{r}_2(0+2\pi - t)\\ &= \left[ 2+\cos \left( 2\pi - t \right) \right] \,\mathbf{i} + \sin \left( 2\pi - t \right)\,\mathbf{j}\\ & = \left( 2+\cos t\right)\,\mathbf{i} -\sin t \,\mathbf{j} \end{align*} \] \[ \begin{align*} x &= 2+\cos t\\ dx & = -\sin t\,dt\\ y &= -\sin t\\ dy &= -\cos t\,dt \end{align*} \] Similarmente para $\delta R_3^-$: \[ \begin{align*} x &= \cos t-2\\ dx & = -\sin t\,dt\\ y &= -\sin t\\ dy &= -\cos t\,dt \end{align*} \] de forma que \[ \begin{align*} \oint_{\delta R^+} \mathbf{F} \cdot d\mathbf{s} &= \int_0^{2\pi} \left( -4\sin t \right)\left( -4\sin t \right)dt + \left( 4\cos t \right)\left( 4\cos t \right)dt\\ &= \int_0^{2\pi} 4dt\\ &= 32\pi\\ \oint_{\delta R_2^-} \mathbf{F} \cdot d\mathbf{s} &= \int_0^{2\pi} \left( \sin t \right)\left( -\sin t \right)\,dt + \left( 2+\cos t \right)\left( -\cos t \right)\,dt\\ &= -2\int_0^{2\pi}\cos t\,dt - \int_0{2\pi}dt\\ &= -2\pi\\ \oint_{\delta R_3^-} \mathbf{F} \cdot d\mathbf{s} &= \int_0^{2\pi} \left( \sin t \right)\left( -\sin t \right)dt + \left( \cos t-2 \right)\left( -\cos t \right)dt\\ &= 2\int_0^{2\pi}\cos t\,dt - \int_0{2\pi}dt\\ &= -2\pi\\ \end{align*} \] por tanto \[ \oint_C \mathbf{F} \cdot d\mathbf{s} = 32\pi - 2\pi -2\pi = 28\pi \nonumber \] Pelo teorema de Green vemos que nossa superfície é o resultado de $R-\left( R_2 \cup R_3 \right)$, dessa forma avaliamos o lado direito do teorema \[ \iint_S \left[ \dfrac{\partial \,}{\partial x}\left( x \right) - \dfrac{\partial \,}{\partial y} \left( -y \right)\right]\,dxdy = 2\iint_S dxdy \nonumber \] onde \[ \begin{align*} \iint_S dxdy &= \iint_{\delta R^+} dxdy - \iint_{\delta R_2^-} dxdy- \iint_{\delta R_3^-} dxdy\\ &= A_{\delta R^+} - A_{\delta R_2^-} - A_{\delta R_3^-}\\ &= \pi (4)^2 - \pi (1)^2 - \pi (1)^2\\ & = 14\pi \end{align*} \] por tanto \[ \iint_S \left[ \dfrac{\partial \,}{\partial x}\left( x \right) - \dfrac{\partial \,}{\partial y} \left( -y \right)\right]\,dxdy = 28\pi \nonumber \]

Exemplo 11

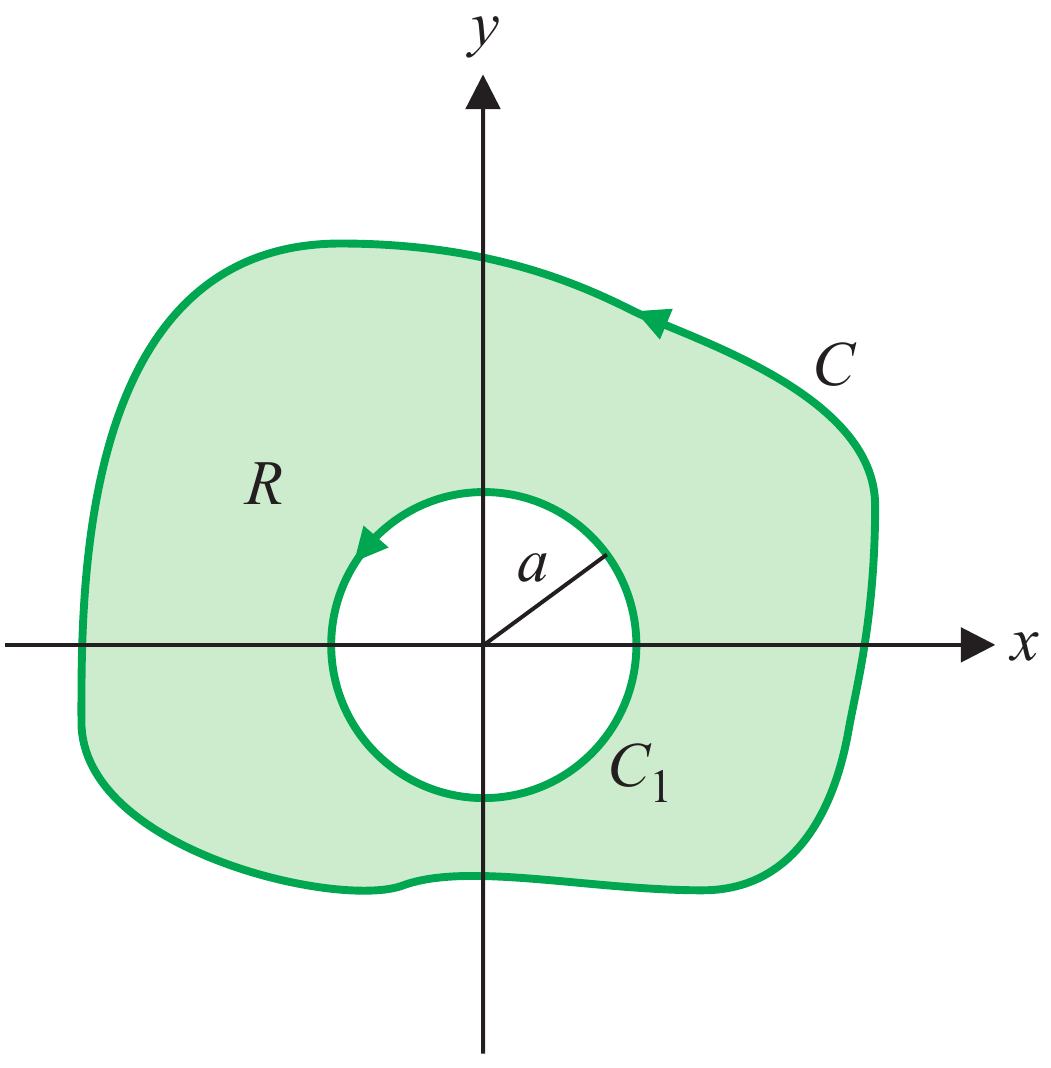
Para \[ \mathbf{F}(x,y) = -\dfrac{y}{x^2+y^2} \,\mathbf{i} + \dfrac{x}{x^2+y^2} \,\mathbf{j} \nonumber \] mostre que $\displaystyle \oint_C \mathbf{F}\cdot d\mathbf{s} = 2\pi$, para qualquer curva simples fechada que inclua a origem dentro da área delimitada.
SOL.
Seja $C$ qualquer curva simples fechada contendo a origem e seja $C_1$ um círculo de raio $a>0$, centrado na origem (e positivamente orientada), onde $a$ é escolhido suficientemente pequeno tal que $C_1$ é interior a $C$, como se ilustra na figura acima. Seja $R$ a região delimitada pelas curvas $C$ e $C_1$ (incluindo as próprias curvas), aplicando o teorema de Green \[ \begin{align*} \oint_C \mathbf{F}\cdot d\mathbf{s} - \oint_{C_1} \mathbf{F}\cdot d\mathbf{s} =& \oint_{\delta R} \mathbf{F}\cdot d\mathbf{s}\\ =& \iint_R \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y} \right)\,dxdy\\ =&\int_R \left[ \dfrac{\left( 1 \right)\left( x^2+y^2 \right)-\left( x \right)\left( 2x \right)}{\left( x^2+y^2 \right)^2} - \dfrac{\left( -1 \right)\left( x^2+y^2 \right)-\left( y \right)\left( 2y \right)}{\left( x^2+y^2 \right)^2} \right]dxdy\\ &=0 \end{align*} \] por tanto \[ \oint_C \mathbf{F}\cdot d\mathbf{s} = \oint_{C_1} \mathbf{F}\cdot d\mathbf{s} \nonumber \] Como $\displaystyle C_1: \mathbf{r}_1(t) =a\cos t \,\mathbf{i} + a\sin t\,\mathbf{j}$, temos \[ \begin{align*} \oint_{C_1} \mathbf{F}\cdot d\mathbf{s} &= \dfrac{1}{a^2}\int_0^{2\pi}\left( -a\sin t\,\mathbf{i} + a\cos t\,\mathbf{j} \right)\cdot \left( -a\sin t\,\mathbf{i} +a\cos t\,\mathbf{j} \right)dt\\ &= 2\pi \end{align*} \]

Exemplo 12

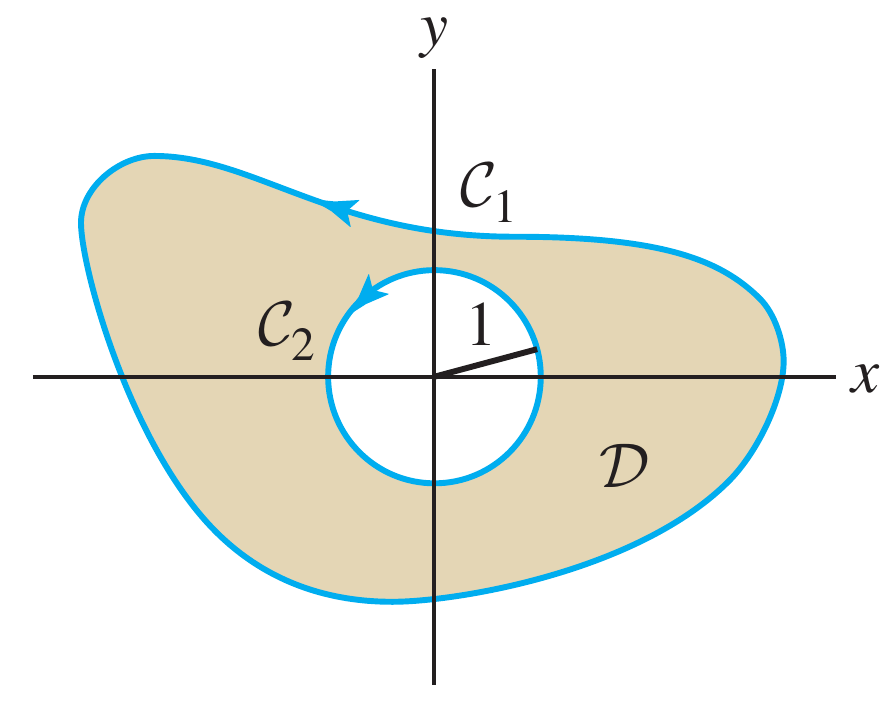
Avalie $\displaystyle \oint_{C_1} \mathbf{F}\cdot d\mathbf{s}$, se $\displaystyle \mathbf{F}(x,y) \left( x-y \right) \,\mathbf{i} + \left( x+y^3 \right)\,\mathbf{j}$ e $C_1$ e a fronteira externa da curva orientada em sentido anti horário. Assuma que o domínio $D$ mostrado na figura ao lado tem área 8.
SOL.
No podemos calcular diretamente a integral de linha ao longo da curva $C_1$ porque nem mesmo foi especificada qual é a curva, mas podemos utilizar $\delta D=C_1 - C_2$ e do teorema de Green \[ \begin{align*} \oint_{C_1} \mathbf{F}\cdot d\mathbf{s} - \oint_{C_2} \mathbf{F}\cdot d\mathbf{s} &= \iint_D \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y}\right)\,dxdy\\ &= \iint_D \left[ \dfrac{\partial \,}{\partial x}\left( x+y^3 \right) - \dfrac{\partial \,}{\partial y} \left( x-y \right)\right]\,dxdy\\ &= \iint_D 2dxdy\\ &=2\text{ área de D}\\ &=16 \end{align*} \] Parametrizando a curva $C_2: \mathbf{r}_2(t) = \cos t \,\mathbf{i} + \sin t\,\mathbf{j}$, temos \[ \begin{align*} \mathbf{F}\cdot\mathbf{v} &= \left(\cos t-\sin t,\,\cos t+\sin^3 t \right)\cdot \left( \sin t,\,\cos t \right)\\ &= -\sin t\cos t + \sin^2 t + \cos^2t+\sin^3 t\cos t\\ &= 1 - \sin t \cos t + \sin^3\cos t \end{align*} \] por tanto \[ \oint_{C_2} \mathbf{F}\cdot d\mathbf{s} = \int_0^{2\pi} \left( 1 - \sin t \cos t + \sin^3\cos t\right)dt = \int_0^{2\pi}dt=2\pi \nonumber \] onde utilizei que a integral de $\sin t \cos t$ e $\sin^3 t \cos t$ é zero. Dessa forma \[ \oint_{C_1} \mathbf{F}\cdot d\mathbf{s} = 16 + 2\pi \nonumber \]