Esferas
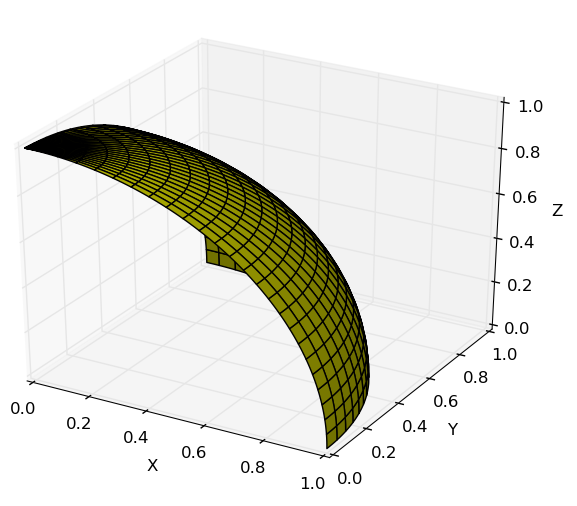
Exemplo 01
Exemplo 01
Parametrize $\displaystyle x^2+y^2+z^2=a^2$, que está no primeiro octante.
SOL.
Utilizando coordenadas esféricas:
\[
\mathbf{r}(u,v) = a \cos \,u\;\sin\, v \,\mathbf{i} + a \sin \,u\;\sin\, v\,\mathbf{j} + a \cos\, v\,\mathbf{k}
\nonumber
\]
A escolha dos limites das variáveis é tal que é desenhada a calota esférica desejada:
\[
\begin{array}{ccccc}
0 & \leq & u &\leq &\dfrac{\pi}{2}\\
0 & \leq & v &\leq &\dfrac{\pi}{2}
\end{array}
\nonumber
\]
Utilizando a parametrização da Diva
\[
\mathbf{r}(u,v) = a \cos \,u\;\cos\, v \,\mathbf{i} + a \sin \,u\;\cos\, v\,\mathbf{j} + a \sin\, v\,\mathbf{k}
\nonumber
\]
A escolha dos limites das variáveis é tal que é desenhada a calota esférica desejada:
\[
\begin{array}{ccccc}
0 & \leq & u &\leq &\dfrac{\pi}{2}\\
0 & \leq & v &\leq &\dfrac{\pi}{2}
\end{array}
\nonumber
\]
)
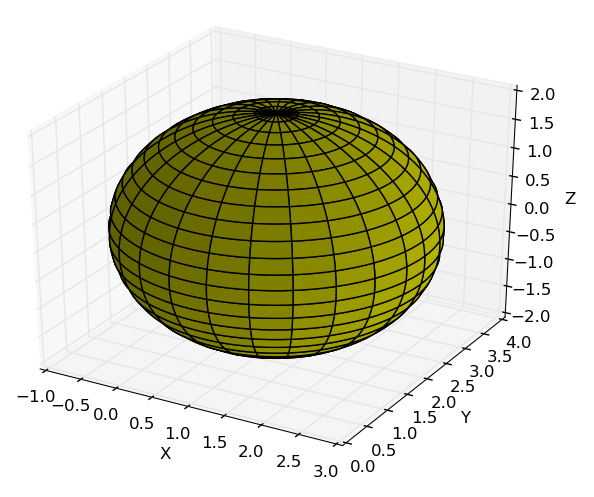
Exemplo 02
Determine a parametrização de $\displaystyle x^2 + y^2+z^2=16$, para $z \geq 2$
SOL.
)
)
Exemplo 03
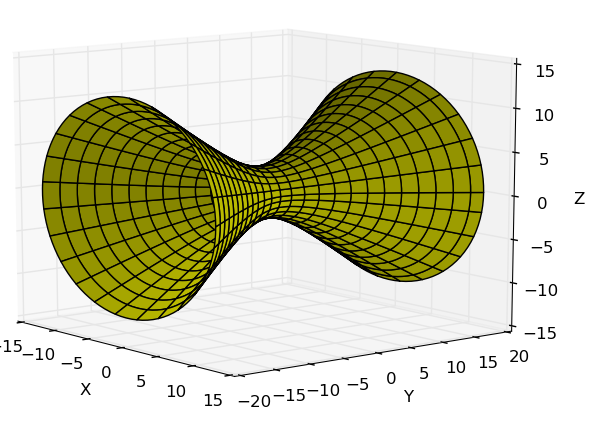
Seja $\displaystyle x^2-2x+y^2-4y+z^2+1=0$, encontre uma parametrização.
SOL.
Neste problema devemos completar o quadrado:
\[
\begin{align*}
x^2-2x+y^2-4y+z^2+1&=0\\
x^2-2x+1-1+y^2-4y+4-4+z^2+1&=0\\
\left( x-1 \right)^2 + \left( y-2 \right)^2+z^2&=4
\end{align*}
\]
o que implica que estamos frente a equação cartesiana de uma circunferência de raio 2 e origem em $\left( 1,\,2,\,0 \right)$, dessa forma as equações paramétricas são
\[
\begin{align*}
x =& 1 + 2 \sin\, v \cos \,u\\
y =& 2 + 2 \sin \,v\;\sin\, u\\
z =& 2\cos v
\end{align*}
\]
com
\[
\begin{array}{ccccc}
0 & \leq & u &\leq &2\pi\\
0 & \leq & v &\leq &\pi
\end{array}
\nonumber
\]
)
Cilindros
Exemplo 04
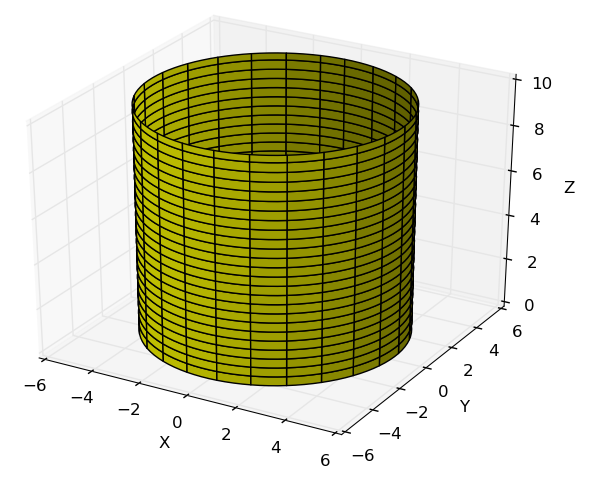
Obter uma parametrização do cilindro $x^2+y^2=25$ entre os planos $z=0$ e $z=10$
SOL.
Neste exemplo se observa que a diretriz do cilindro é um circunferência, que no plano $z=0$ tem por equação
\[
\vec{\beta}(u) =5\cos u \,\mathbf{i} +5\sin u \,\mathbf{j},\;\;\;0\leq u \leq 2\pi
\nonumber
\]
Um dos vetores que fazem parte da geratriz é aquele que vai desde $\left( 5,0,0 \right)$ até $\left( 5,0,10 \right)$, por tanto
\[
\vec{q} = 10 \,\mathbf{k}
\nonumber
\]
dessa forma a equação do cilindro é
\[
\begin{align*}
\mathbf{r}(u,v) =& \vec{\beta}(u) + v\vec{q}\\
=& 5\cos u \,\mathbf{i} +5\sin u \,\mathbf{j} + 10\,v \,\mathbf{k}
\end{align*}
\]
onde
\[
\begin{array}{ccccc}
0 & \leq & u &\leq &2\pi\\
0 & \leq & v & < & 1
\end{array}
\nonumber
\]
note que a escolha de $v_f=1$ garante que a última circunferência acontece quando $z=10$.
)
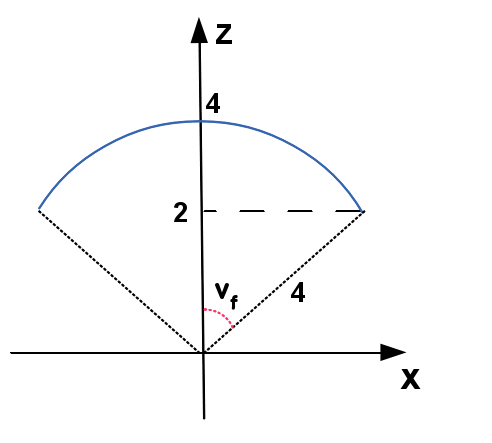
Exemplo 05
Obter uma parametrização do cilindro $4x^2+y^2=16$, que está entre os planos $z=5$ e $z=15$
SOL.
A equação cartesiana descreve um cilindro elíptico:
\[
\begin{align*}
4x^2+y^2=&16\\
\left( \dfrac{x}{2} \right)^2 + \left( \dfrac{y}{4} \right)^2 =&1
\end{align*}
\]
Essa elipse é a equação cartesiana da diretriz de nosso cilindro o qual, na atura de $z=10$ estará passando por
\[
\mathbf{r}(u) = 2\cos u \,\mathbf{i} +4\sin u \,\mathbf{j} + 10 \,\mathbf{k}
\nonumber
\]
Um dos possíveis vetores diretriz é aquele que vai desde $\left( 2,0,5 \right)$ até $\left( 2,0,15 \right)$, por tanto
\[
\vec{q} = 10 \,\mathbf{k}
\nonumber
\]
dessa forma a equação do cilindro é
\[
\begin{align*}
\mathbf{r}(u,v) =& \vec{\beta}(u) + v\vec{q}\\
=& 2\cos u \,\mathbf{i} + 4\sin u \,\mathbf{j} + 10(1+v) \,\mathbf{k}
\end{align*}
\]
onde
\[
\begin{array}{ccccc}
0 & \leq & u &\leq &2\pi\\
-0.5 & \leq & v & < & 0.5
\end{array}
\nonumber
\]
note que a escolha dos limites de $v$ garante que a última circunferência acontece quando $z=15$ e primeira em $z=5$.
)
Exemplo 06
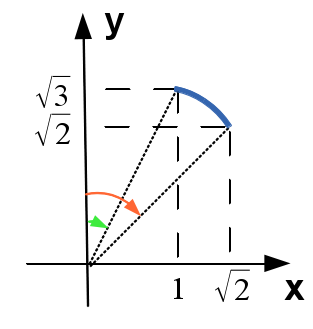
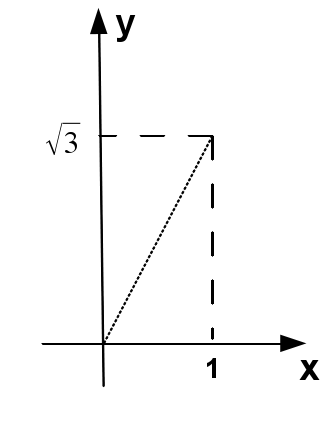
Obter uma parametrização da parte $x^2+y^2=4$, $0\leq z \leq 5$, delimitada pelos semiplanos $y=x$ e $y=\sqrt{3}x$, com $z \geq 0$.
)
SOL.
Devido a restrição imposta pelos planos, o cilindro fica delimitado entre um $u_{min}$ e um $u_{max}$. Para determinar esses ângulos vamos projetar o cilindro no plano $xy$. Observe que as equações dos planos nos indicam de imediato qual é o ângulo de inclinação de cada plano em relação ao eixo $x$. No caso da equação $y=x$ temos \[ \begin{align*} \tan \left( \dfrac{\pi}{2} - u_{max} \right) =& 1\\ u_{max}=&\dfrac{\pi}{2} - \frac{\pi}{4}\\ =& \frac{\pi}{4} \end{align*} \] No caso da equação $y=\sqrt{3}x$ temos \[ \begin{align*} \tan \left( \dfrac{\pi}{2} - u_{min} \right) =& \sqrt{3}\\ u_{min}=&\dfrac{\pi}{2} - \frac{\pi}{3}\\ =& \dfrac{\pi}{6} \end{align*} \] A geratriz de nosso cilindro é \[ \vec{\beta}(u) =2\cos u \,\mathbf{i} +2\sin u \,\mathbf{j},\;\;\;0\leq u \leq 2\pi \nonumber \] e uma diretriz será desde $\left( 2,0,0 \right)$ até $\left( 2,0,5 \right)$, por tanto \[ \vec{q} = 5 \,\mathbf{k} \nonumber \] dessa forma a equação do cilindro é \[ \begin{align*} \mathbf{r}(u,v) =& \vec{\beta}(u) + v\vec{q}\\ =& 2\cos u \,\mathbf{i} +2\sin u \,\mathbf{j} + 5\,v \,\mathbf{k} \end{align*} \] onde \[ \begin{array}{ccccc} \frac{\pi}{3} & \leq & u &\leq &\frac{\pi}{4}\\ 0 & \leq & v & < & 1 \end{array} \nonumber \]
)
Exemplo 07
Se a diretriz de um cilindro dado é $y=x^2$, obter uma parametrização para o cilindro se $|\,x\,| \leq 2$ e $0\leq |\,z\,| \leq 8$
SOL.
Neste problema a nossa diretriz está dada pela parametrização ($z=0$)
\[
\begin{cases}
x =& u\\
y =& u^2
\end{cases}
\nonumber
\]
Uma das geratrizes que podemos definir fica entre $(0,0,0)$ e $(0,0,8)$, assim
\[
\vec{q} = 8 \,\mathbf{k}
\nonumber
\]
dessa forma a equação do cilindro é
\[
\begin{align*}
\mathbf{r}(u,v) =& \vec{\beta}(u) + v\vec{q}\\
=& u \,\mathbf{i} + u^2 \,\mathbf{j} + 8\,v \,\mathbf{k}
\end{align*}
\]
onde
\[
\begin{array}{ccccc}
-2 & \leq & u &\leq &2\\
0 & \leq & v & < & 1
\end{array}
\nonumber
\]
)
Cones
Exemplo 08
Obter uma parametrização do cone gerado pela semi-reta $z=\sqrt{3}y$, $y>0$, quando está gira em torno do eixo positivo $z$
SOL.
)
)
Exemplo 09
Obter uma parametrização do cone $z=-\sqrt{x^2+y^2}$ para $-2\leq z \leq 0$
SOL.
Essa é a equação cartesiana de um cone, como
\[
\begin{align*}
r^2 =& x^2+y^2\\
r =& -z
\end{align*}
\]
assim, quando $z=-2$ o raio da circunferência do cone nessa altura é $r=2$, de forma que a diretriz estará dada por
\[
\vec{\beta}(u) = 2\sin u \,\mathbf{i} + 2\cos u \,\mathbf{j} -2 \, \mathbf{k}
\nonumber
\]
como a origem está em $\vec{r}_0=(0,0,0)$, temos que a equação paramétrica do cone será
\[
\vec{r}(u,v) = 2v\sin u \,\mathbf{i} + 2v\cos u \,\mathbf{j} -2 v\,\mathbf{k}
\nonumber
\]
com
\[
\begin{array}{ccccc}
0 & \leq & u &\leq &2\pi\\
0 & \leq & v & < & 1
\end{array}
\nonumber
\]
)
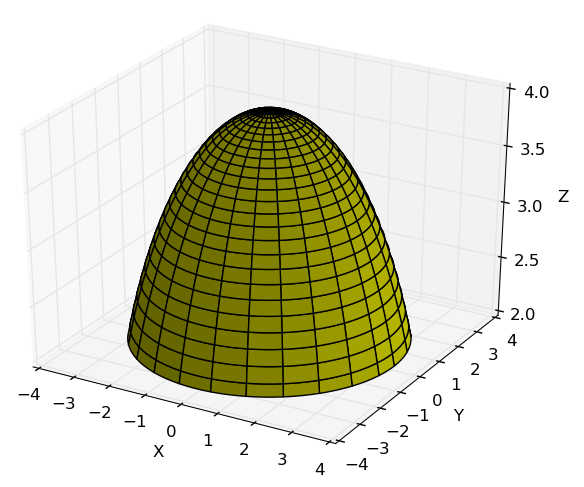
Exemplo 10
Obter uma parametrização do cone $4x^2+9z^2=9y^2$
SOL.
\[
\begin{align*}
4x^2+9z^2=&9y^2\\
\dfrac{4}{9}x^2+z^2=&y^2\\
\left( \dfrac{x}{\frac{3}{2}} \right)^2+z^2=&y^2
\end{align*}
\]
Por tanto a diretriz de nosso cone é uma parábola com semi eixo menor igual a 1 e o semi eixo maior igual a 3/2. Note que quando $x=0, \, y=0 \Rightarrow z=0$ o qual indica que o vértice está em $z=0$. Para determinar uma geratriz escolhemos uma que passe pelo plano $x=0$, onde $z=y$, assim resulta conveniente $z=y=1$, por tanto uma parametrização adequada para esse cone é
\[
\vec{r}(u,v) = \dfrac{3}{2}v\cos u \,\mathbf{i} + v \,\mathbf{j} + \cos u \,\mathbf{k}
\nonumber
\]
com
\[
\begin{array}{ccccc}
0 & \leq & u &\leq &2\pi\\
-\infty & < & v & < & \infty
\end{array}
\nonumber
\]
)
Exemplo 11
Determinar as equações paramétricas do cone $C$ com vértice no ponto $V=(-1,1,1)$ e que tem como diretriz a curva dada por $\displaystyle x^2-4z-4=0$, $y=0$
SOL.
A nossa diretriz está dada pela equação $\displaystyle z=\dfrac{1}{4}x^2-1$ a qual tem a seguinte parametrização
\[
\begin{cases}
x =& u\\
y =& \dfrac{1}{4}u^2-1
\end{cases}
\nonumber
\]
Considerando as coordenadas do vértice obtemos a equação para o cone:
\[
\begin{align*}
\mathbf{r}(u,v) =& \left( -1,1,1 \right) + \left\{ \left[ u,\left(\dfrac{1}{4}u^2-1\right),0 \right] - \left( -1,1,1 \right)\right\} v\\
\mathbf{r}(u,v)=& \left[ \left( u+1 \right)v -1 \right] \,\mathbf{i} + \left( \dfrac{u^2v}{4}+1\right)\,\mathbf{j} + \left( v+1 \right) \,\mathbf{k}
\end{align*}
\]
)
Superfícies de revolução
Exemplo 12
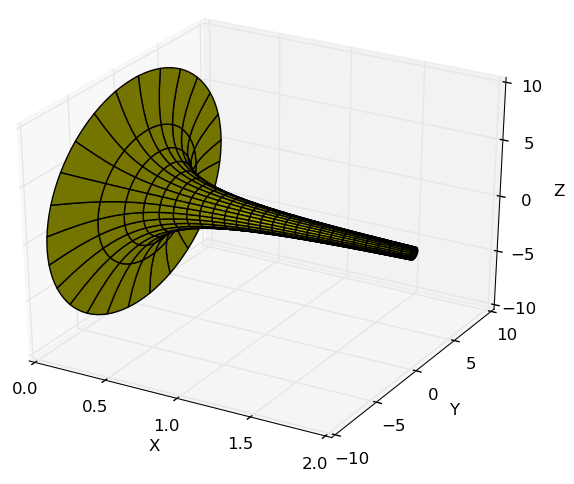
Determine equações paramétricas para a superfície gerada pela revolução da curva $y=1/x$ em torno do eixo $x$, entre $0< x < 2$
SOL.
Como a função já está expressada em termos da variável que define o eixo de rotação, podemos escrever diretamente a parametrização
\[
\begin{cases}
x =& u\\
y =& \dfrac{1}{u}\, \cos v\\
z =& \dfrac{1}{u}\, \sin v\\
\end{cases}
\nonumber
\]
com
\[
\begin{array}{ccccc}
0 & \leq & v &\leq &2\pi\\
0 & < & u & \leq & 2
\end{array}
\nonumber
\]
)
Exemplo 13
Determine equações paramétricas para a superfície do cone circular reto $z^2=x^2+y^2$ que está entre os planos $z=1$ e $z=4$
SOL.
Para resolver este problema podemos encarar ele de duas formas diferentes, na primeira forma encaramos diretamente a parametrização do cone cuidando dos limites da variável que estende o vetor da geratriz. Na segunda forma encaramos o problema como o de uma reta definida entre dois pontos e que rota em torno do eixo de $z$. Observe, no entanto, que no fim ambas metodologias levam à mesma solução.
Parametrizando o cone
Neste caso o cone é um cone circular reto com diretriz paralela ao plano $xy$, que para o caso de $z=4$ está dada por \[ \vec{\beta}(u) = 4\cos u \,\mathbf{i} + 4\sin u \,\mathbf{j} + 4\,\mathbf{k} \nonumber \] A origem de nosso cone acontece no ponto $\vec{r}_0 = (0,0,0)$, por tanto \[ \vec{r}(u,v) = 4v\cos u \,\mathbf{i} + 4v\sin u \,\mathbf{j} + 4v\,\mathbf{k} \nonumber \] Tipicamente a escolha dos limites para $v$ na parametrização anterior é $0 \leq v \leq 1$, mas isso implica em que nosso cone sera formado por infinitas circunferências de raio desde zero até 4 o qual está em desacordo com a proposição do problema. Nosso raio inicial deve ser aquele que acontece para $z=1=x^2+y^2$ ou seja, $r=1$. Essa diretriz tem por equação \[ \vec{\beta}(u) = \cos u \,\mathbf{i} + \sin u \,\mathbf{j} + 1\,\mathbf{k} \nonumber \] o qual implica que $v=\frac{1}{4}$, dessa forma
)
Parametrizando a linha de revolução
Para parametrizar a cone cortado podemos considerar uma linha que este sobre o plano $xz$, nesse caso a equação cartesiana do cone reduz para $x=z$. Como nosso eixo de rotação será o eixo $z$ escrevemos \[ \begin{cases} x =& u\,\cos v\\ y =& u\, \sin v\\ z =& u\\ \end{cases} \nonumber \] com \[ \begin{array}{ccccc} 0 & \leq & v &\leq &2\pi\\ 1 & \leq & u & \leq & 4 \end{array} \nonumber \]
)
Exemplo 14
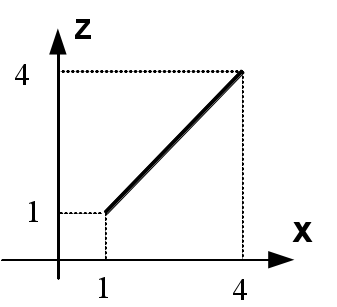
Dada a hipérbole
\[
\left(\dfrac{x}{3}\right)^2 - \left(\dfrac{y}{5}\right)^2=1
\nonumber
\]
expresse de forma paramétrica a superfície resultante da rotação dessa curva em torno eixo $y$.
SOL.
A equação dessa hipérbole gera o seguinte gráfico no plano $z=0$
)
)
Exemplo 15
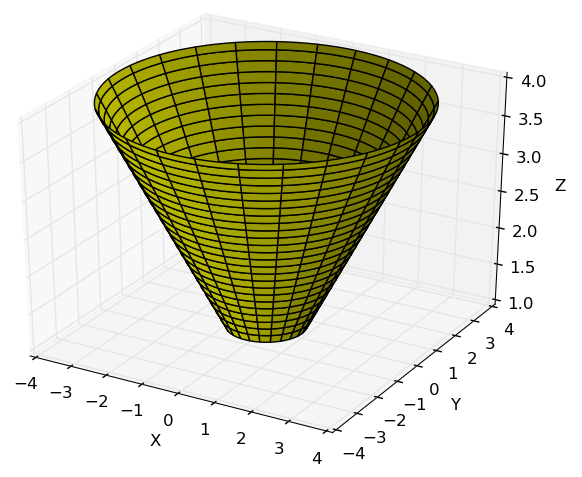
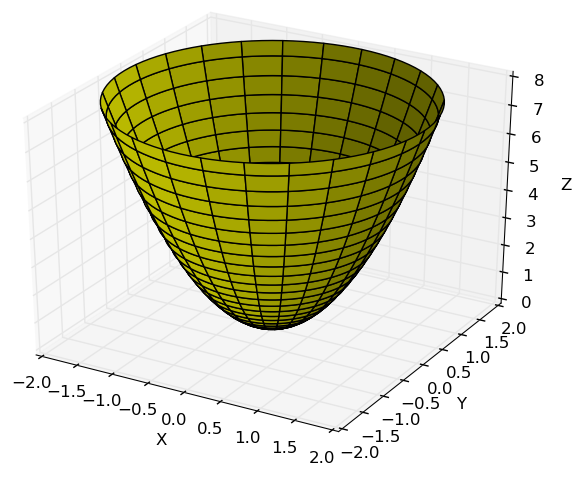
Parametrize o paraboloide $z=2\left(x^2 + y^2\right)$, abaixo do plano z=8
Sol.
\[
\begin{align*}
x =& \sqrt{\dfrac{u}{2}}\cos \,v\\
y =& \sqrt{\dfrac{u}{2}}\sin \,v\\
z =& u
\end{align*}
\]
onde $0\leq v \leq 2\pi$ e $0\leq u \leq 8$.
)
Outras parametrizações
Exemplo 16
-
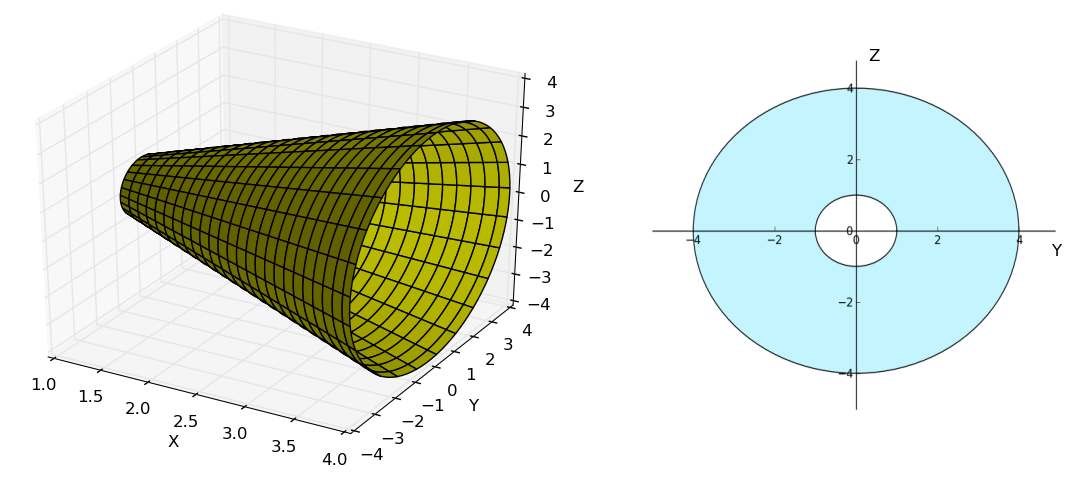
Obter uma parametrização da parte do cone $x^2=y^2+z^2$, que está entre os planos $x=1$ e $x=1$
Sol.
A partir da equação cartesiana escolhemos \[ y = u,\;\;\;\;\;\;\; z=v \nonumber \] isso nos leva então para \[ x = \sqrt{u^2+v^2} \nonumber \] onde o sinal positivo na raiz indica que escolhemos o cone superiorPara estabelecer os limites dessa superfície observamos a projeção no plano $yz$, note que os valores são tais que a superfície projeta duas a área entre as circunferências de raio $4$ e $1$, dessa forma a escolha dos dados deve ser tal que \[ 1 \leq u^2+v^2 \leq 16 \nonumber \]
Se tivéssemos escolhido a parametrização de uma figura de rotação a solução seria bem mais simples: \[ \begin{align*} x =& u\\ y =& u\cos \,v\\ z =& u\sin \,v \end{align*} \] onde $1\leq u < 4$ e $0\leq v \leq 2\pi$
)
Exemplo 17
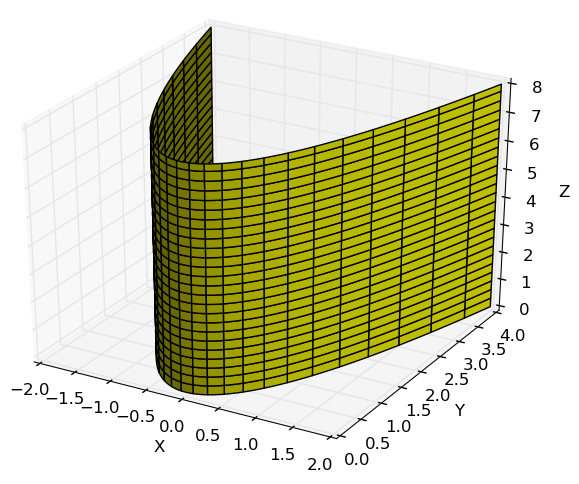
(Problema da Diva 10.3.45) Escreve uma representação paramétrica para a superfície
- Do cilindro cortado
- Do plano inscrito no cilindro
SOL.
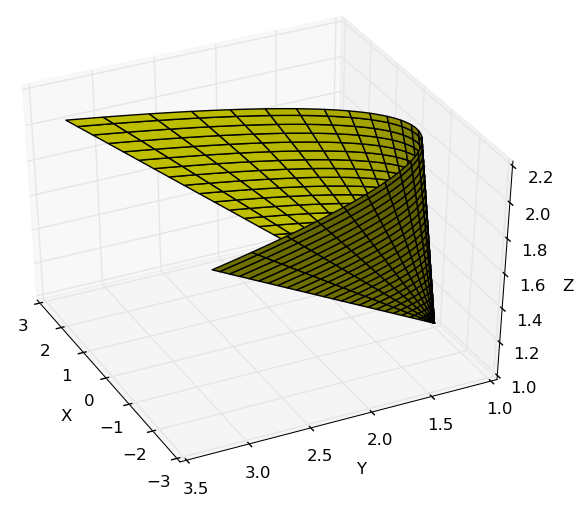
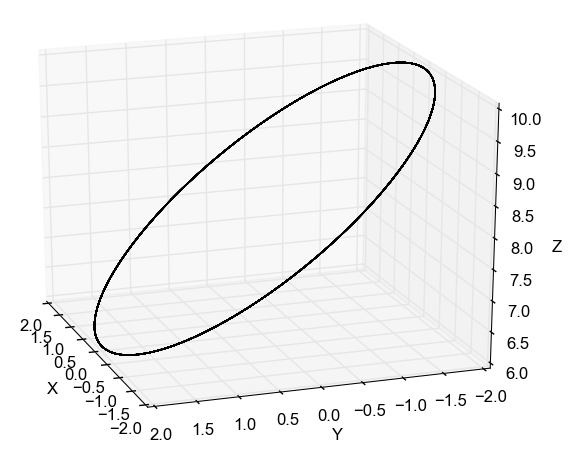
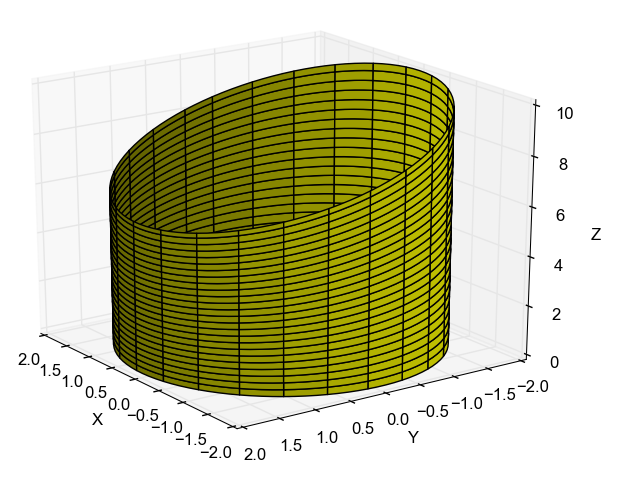
Da teoria sabemos que a parametrização de um cilindro está dada pela parametrização da diretriz, que no caso é uma circunferência de raio 2 no plano $xy$ e por tanto dada por \[ \beta(u) = 2\cos\,u\,\mathbf{i} + 2\sin\,u \,\mathbf{j}, \nonumber \] mas a equação das retas geratrizes, que geralmente são da forma $z=v$, contudo, para o caso deste problema sabemos que o cilindro está limitado pelo plano $z=8-y$, que em termos da parametrização da diretriz escrevemos como \[ z = 8-y=8-2\cos\,u \nonumber \] A curva desenhada pela interseção dessas superfícies é uma elipse inclinada
)
)
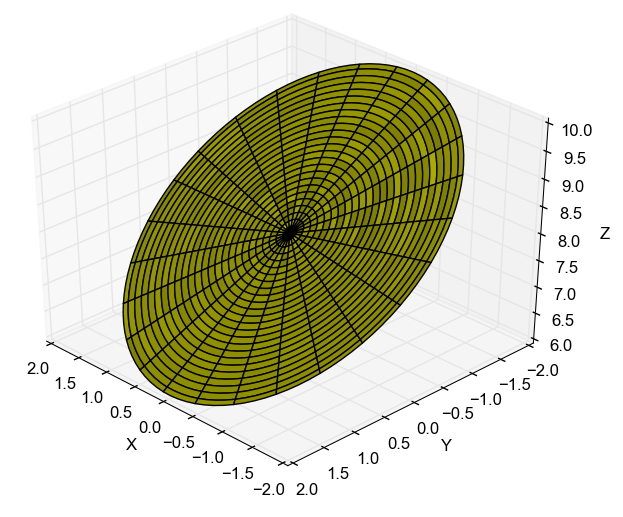
Para o caso do plano que fica delimitado pelo cilindro teremos que ele resulta da união de varias curvas de níveis projetadas em $z=8-y$. Cada curva de nível vai ser uma elipse as quais vão variar seu raio, por tanto a equação para cada uma delas será \[ r_{cn}(u,v) = v\cos\,u\,\mathbf{i} + v\sin\,u \,\mathbf{j}, \nonumber \] como o menor raio possível é $0$ e o maior raio possível é $2$, então $0\leq v \leq 2$. Substituindo o $y$ em $z$, temos $z=8-v\sin\,u$, por tanto a equação do plano será \[ r(u,v) = v\cos\,u\,\mathbf{i} + v\sin\,u \,\mathbf{j}+ \left( 8-v\sin\,u \right)\,\mathbf{k} \nonumber \]
)