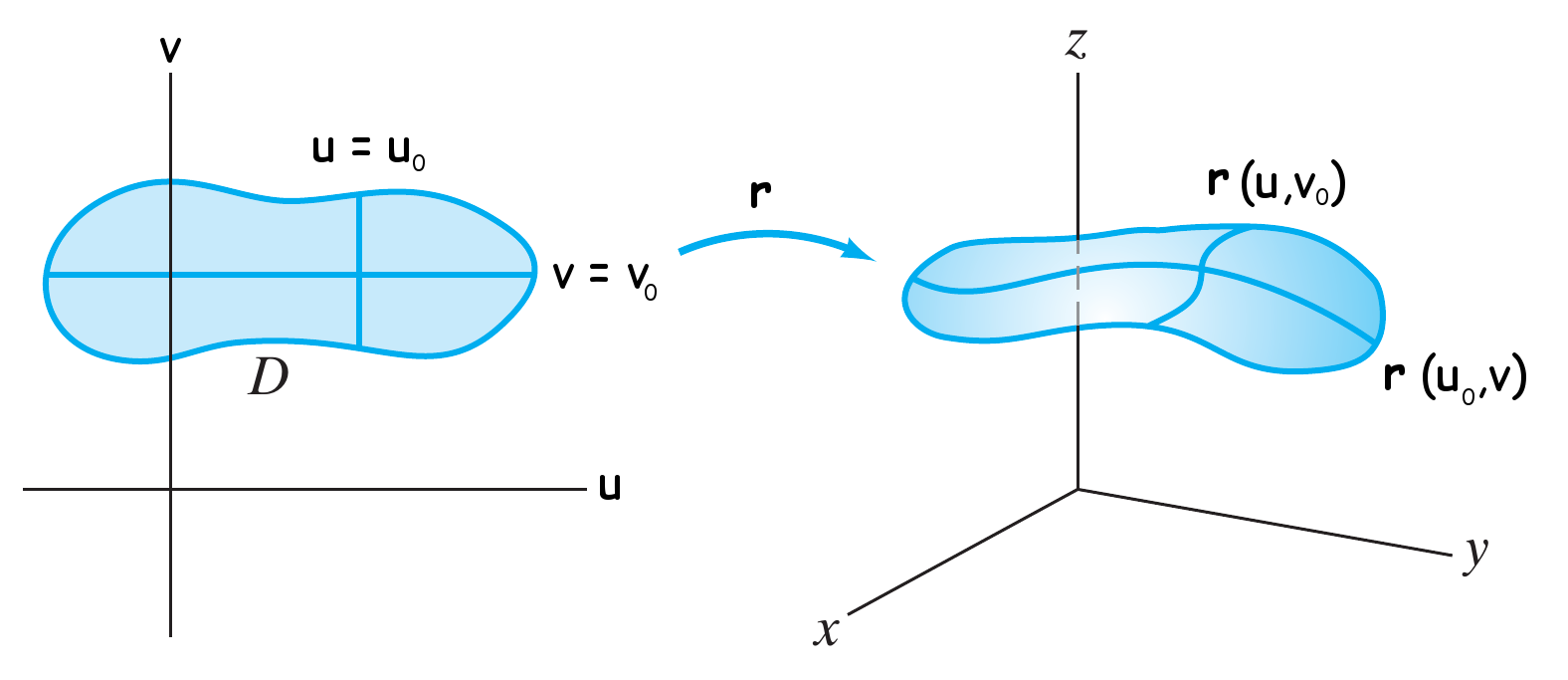
Curvas coordenadas

Seja $S$ uma superfície parametrizada por $\mathbf{r}:D\to \mathbb{R}^3$. Se fixamos $v=v_0$ e só permitimos variar $u$, obteremos uma mapeamento continuo \[ u \mapsto \mathbf{r}(u,v_0) \nonumber \] cuja imagem é uma curva que fica sobre $S$ a cual chamaremos de u-curva ou curva coordenada u em $v_0$. Similarmente podemos fixar $u=u_0$ e obteremos um mapeamento \[ v \mapsto \mathbf{r}(u_0,v) \nonumber \] cuja imagem é a v-curva em $u=u_0$.

Às curvas resultantes denominamos genericamente de curvas coordenadas.

Exemplo 01

Determine a curva coordenadas da esfera $x^2+y^2+z^2=4$, que passa por $P=(2,0,0)$
SOL.
A representação vetorial da superfície (utilizando a parametrização da diva) é \[ \mathbf{r}(u,v) = 2\cos\,u\cos\,v \,\mathbf{i} + 2\,sin\,u\sin\,v \,\mathbf{j} + 2\sin\,v \,\mathbf{k},\;\;\;\;\;0\leq u \leq 2\pi\;\; -\dfrac{\pi}{2}\leq v \leq \dfrac{\pi}{2} \nonumber \] O ponto $P=(2,0,0)$ implica em \[ \begin{array}{ccccc} z = 0 & \Rightarrow & \sin v = 0 & \Rightarrow & v = 0\\ y = 0 & \Rightarrow & \sin u = 0 & \Rightarrow & u = 0\\ x = 2 & \Rightarrow & \cos u = 1 & \Rightarrow & u = 0 \nonumber \end{array} \] dessa forma, a curva $u$ no ponto $P=(2,0,0)$ é \[ \mathbf{r}(u,0) = 2\cos\,u \,\mathbf{i} + 2\,sin\,u \,\mathbf{j},\;\;\;\;\;0\leq u \leq 2\pi \nonumber \] similarmente a curva $v$ \[ \mathbf{r}(0,v) = 2\cos\,v \,\mathbf{i} + 2\sin\,v \,\mathbf{j},\;\;\;\;\;-\dfrac{\pi}{2}\leq v \leq \dfrac{\pi}{2} \nonumber \]

Vetor normal e plano tangente

Superfícies suaves, vetores normais

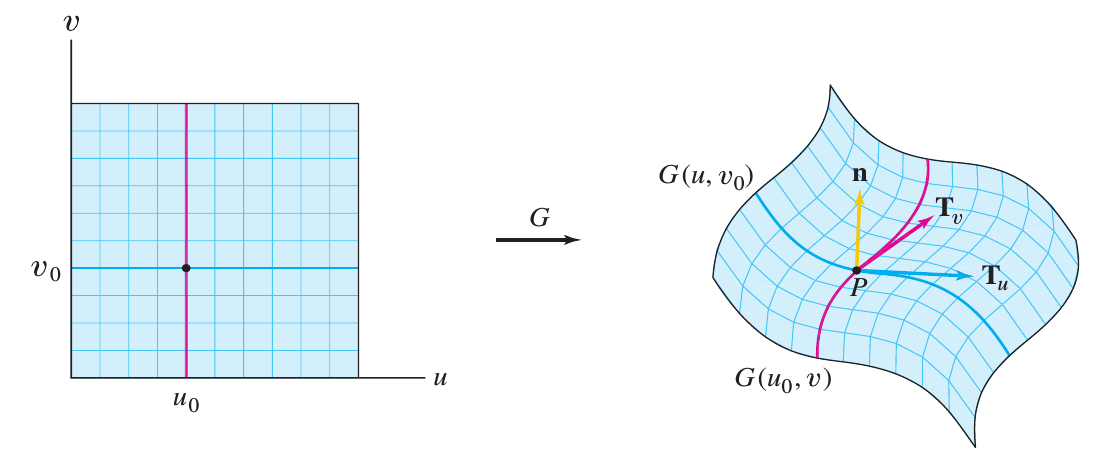
Se $\mathbf{r}=\left< x(u,v),\,y(u,v),\,z(u,v)\right>$, onde $(u,v)\in D$, é um mapeamento diferenciável (ou de classe $C^1$), isto é, cada componente é diferenciável, então dizemos que a superfície $S=\mathbf{r}(D)$ é diferenciável (ou de classe $C^1$). Neste caso, as $u$-curvas: $\mathbf{r}(u,v_0)$, e $v$-curvas: $\mathbf{r}(u_0,v)$, tem tangente tangentes bem definidas em $D$.

Para calcular o vetor tangente, $\mathbf{T}_u$, à $u$-curva $\mathbf{r}(u,v_0)$ em $(u_0,v_0)$, calculamos a deriva das componentes de $\mathbf{r}$ em relação a $u$ e avaliamos em $(u_0,v_0)$: \[ \mathbf{T}_u = \dfrac{\partial \mathbf{r}}{\partial u}\left( u_0,v_0 \right)=\dfrac{\partial x}{\partial u}\left( u_0,v_0 \right) \,\mathbf{i} + \dfrac{\partial y}{\partial u}\left( u_0,v_0 \right) \,\mathbf{j} + \dfrac{\partial z}{\partial u}\left( u_0,v_0 \right) \,\mathbf{k} \nonumber \] Similarmente, o vetor tangente, $\mathbf{T}_v$, à $v$-curva $\mathbf{r}(u_0,v)$ em $(u_0,v_0)$ se calcula deriva das componentes de $\mathbf{r}$ em relação a $v$ e avaliamos em $(u_0,v_0)$: \[ \mathbf{T}_v = \dfrac{\partial \mathbf{r}}{\partial v}\left( u_0,v_0 \right)=\dfrac{\partial x}{\partial v}\left( u_0,v_0 \right) \,\mathbf{i} + \dfrac{\partial y}{\partial v}\left( u_0,v_0 \right) \,\mathbf{j} + \dfrac{\partial z}{\partial v}\left( u_0,v_0 \right) \,\mathbf{k} \nonumber \] Como $\mathbf{T}_u$ e $\mathbf{T}_v$ são ambos tangentes à superfície $S$ em $\left( u_0,v_0 \right)$, o produto vetorial $\mathbf{T}_u \times \mathbf{T}_v$ deve ser normal à superfície $S$ em $\left( u_0,v_0 \right)$, desde que ele não seja zero.

Definição

A superfície parametrizada $S=\mathbf{r}(D)$ é suave ou regular em $\mathbf{r}\left( u_0,v_0 \right)$ se o mapeamento é de classe $C^1$ na vizinhança de $\left( u_0,v_0 \right)$ e se o vetor \[ n\left( u_0,v_0 \right) = \mathbf{T}_u\left( u_0,v_0 \right) \times \mathbf{T}_v\left( u_0,v_0 \right) \neq \mathbf{0} \nonumber \] Se $S$ é suave para qualquer ponto $\mathbf{r}\left( u_0,v_0 \right)\in S$ nos referiremos a $S$ como sendo uma superfície suave ou regular (sem arestas).

Equação da reta normal

Como para todos os pontos, $\displaystyle \left( u_0,v_0 \right)$, da superfície $S$ podemos calcular o vetor normal, então a reta que passa pelo ponto $\displaystyle \left( u_0,v_0 \right)$ e é normal à superfície tem a seguinte equação paramétrica \[ \mathbf{r}(t) = \mathbf{r}\left( u_0,v_0 \right) + t\, n\left( u_0,v_0 \right) \nonumber \]

Equação do plano tangente

Podemos utilizar o fato de que $\displaystyle \mathbf{n} = \mathbf{T}_u \times \mathbf{T}_v$ é normal à superfície e a partir disto calcular o plano tangente à superfície

Definição

Se uma superfície parametrizada $\mathbf{r}:\, D\subset \mathbb{R}^2\to \mathbb{R}3$ é regular em $\displaystyle \mathbf{r}\left( u_0,v_0 \right)$, isto é, se $\displaystyle \mathbf{T}_u \times \mathbf{T}_v \neq \mathbf{0}$ em $\displaystyle \left( u_0,v_0 \right)$, definimos o plano tangente da superfície $S$ em $\displaystyle \mathbf{r}\left( u_0,v_0 \right)$ como sendo o plano determinado pelos vetores $\displaystyle \mathbf{T}_u $ e $\displaystyle \mathbf{T}_v$. Assim, $\displaystyle \mathbf{T}_u \times \mathbf{T}_v$ é um vetor normal, $\mathbf{q}$ um vetor que localiza o ponto $\displaystyle \left(x_0,\,y_0,\,z_0\right)$, uma equação do plano tangente sobre a superfície $S$ no ponto $\displaystyle \left(x_0,\,y_0,\,z_0\right)$ está dada por \[ \begin{align*} \mathbf{q} \cdot \mathbf{n} &= 0\\ \left[\left( x-x_0 \right) \,\mathbf{i} + \left( \,y-y_0 \right) \,\mathbf{j} + \left( z-z_0 \right) \,\mathbf{k}\right] \cdot \mathbf{n} &= 0 \end{align*} \] onde $\mathbf{n}$ é avaliado em $\displaystyle \left( u_0,v_0 \right)$; isto é, o plano tangente é o conjunto de pontos $\left(x,\,y,\,z\right)$ que satisfazem a equação anterior. Se as componentes do vetor $\mathbf{n}$ são $\displaystyle \left(n_x, \, n_y\, n_z \right)$, então podemos reescrever a equação anterior como \[ \left( x-x_0 \right)\,n_x + \left( \,y-y_0 \right)\,n_y + \left( z-z_0 \right)\,n_z = 0 \nonumber \]

Superfícies definidas por partes

Dizemos que $S$ é suave por partes se $S$ pode ser dividida em um número finito de partes suaves:

1. Planos, paraboloides, esferas, etc. são suaves
2. O cone não é suave
3. O cubo é suave por partes

Superfícies orientadas

A continuação vamos definir o que é uma superfície de 2 lados

Definição

Uma superfície orientada $S$ é uma superfície de dois lados com um lado especificado como o lado externo ou lado positivo; enquanto que o outro lado é o lado interno ou negativo. Em cada ponto $\displaystyle \left(x,\,y,\,z\right)\in S$ temos definidos 2 vetores normais $\mathbf{n}_1$ e $\mathbf{n}_2$, onde $\mathbf{n}_1 = \mathbf{n}_2$. Cada um desses 2 vetores normais pode ser associado a um dos lados da superfície. Assim, para especificar o lado da superfície $S$, em cada ponto devemos selecionar o ver unitário normal que aponte para fora desde o lado positivo de $S$ no ponto.

O conjunto de todos os vetores normais associados a cada ponto de $S$ são descritos por por uma função que varia continuamente. O campo descrito pelo conjunto de vetores normais, chamamos de campo normal. O vetor unitário normal está definido como \[ \mathbf{n} = \dfrac{\mathbf{T}_u \times \mathbf{T}_v}{\left| \, \mathbf{T}_u \times \mathbf{T}_v \, \right|} \nonumber \] para todos os pontos onde $S$ é suave.

Obviamente, se existem superfícies de 2 lados, existem superfícies de um lado, um exemplo desse tipo de superfície é a fita de Möbius

A fita de Möbius é parametrizada por \[ \begin{align*} x =& \left( 1+ v\cos\dfrac{u}{2} \right)\cos\,u\\ y =& \left( 1+ v\cos\dfrac{u}{2} \right)\sin\,u\\ z =& v\sin\,\dfrac{u}{2} \end{align*} \]

onde $0\leq u\leq 2\pi$ e $\displaystyle -\dfrac{1}{2} \leq v \leq \dfrac{1}{2}$. A partir dessa parametrização obtemos o vetor norma, dado por \[ \begin{align*} n_x =& \sin\,\dfrac{u}{2}\left[ \cos\,u + 2v\, \left( \cos^3 \dfrac{u}{2} - \cos \dfrac{u}{2}\right) \right]\\ n_y =& \dfrac{1}{2}\left[ 4\cos \dfrac{u}{2} - 4\cos^3 \dfrac{u}{2}+v \left( 1+\cos\,u -\cos^2u \right) \right]\\ n_z=& -\cos \dfrac{u}{2} \left( 1+v\cos \dfrac{u}{2} \right) \end{align*} \]

Observe que se escolhemos uma dada $u$-curva, por exemplo quando $v=0$, nos leva à seguinte representação vetorial da normal \[ \mathbf{n}(u,0) = \sin\,\dfrac{u}{2}\,\cos\,u\,\mathbf{i} + 2\left( \cos \dfrac{u}{2} - \cos^3 \dfrac{u}{2}+v\right) \,\mathbf{j} - \cos \dfrac{u}{2}\,\mathbf{k} \nonumber \] assim, para $u=0$ temos que $\mathbf{n}(0,0) =-\mathbf{k}$ e para $u=2\pi$, $\mathbf{n}(0,0) =\mathbf{k}$, ou seja, parece que o vetor normal mudou de direção o que indica que a fita de Möbius é não orientada.

Exemplo 02

Dada \[ \mathbf{r}(u,v) = u\cos\,v \,\mathbf{i} +u\sin\,v \,\mathbf{j} + (u^2-1) \,\mathbf{k},\;\;\;\;0\leq u\leq 4,\;0\leq v\leq 2\pi \nonumber \]

1. Determine, $\mathbf{T}_u$, $\mathbf{T}_v$, $\mathbf{n}$, para $u=2$, $v=\pi/4$.
2. Determine a equação do plano tangente.

SOL.

1. \[ \begin{align*} \mathbf{T}_u =& \dfrac{\partial \mathbf{r}}{\partial u}\\ =& \cos\,v \,\mathbf{i} +\sin\,v \,\mathbf{j} + 2u \,\mathbf{k}\\ \mathbf{T}_v =& \dfrac{\partial \mathbf{r}}{\partial v}\\ =&-u\sin\, v\,\mathbf{i} +u\cos\, v \,\mathbf{j}\\ \mathbf{n} =&\begin{bmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \cos\,v & \sin\,v & 2u\\ -u\sin\, v & u\cos\, v & 0 \end{bmatrix}\\ =& -2u^2\cos\,v\,\mathbf{i} -2h^2\sin\,v \,\mathbf{j} + u \,\mathbf{k} \end{align*} \] com $u=2$, $v=\pi/4$, temos \[ \begin{align*} \mathbf{T}_u \left( 2,\dfrac{\pi}{4} \right) =& \left< \dfrac{\sqrt{2}}{2},\, \dfrac{\sqrt{2}}{2},\,4 \right>\\ \mathbf{T}_v \left( -2,\dfrac{\pi}{4} \right) =& \left< \sqrt{2},\, \sqrt{2},\,0 \right>\\ \mathbf{n} \left( 2,\dfrac{\pi}{4} \right) =& \left< -4\sqrt{2},\, -4\sqrt{2},\,2 \right>\\ \end{align*} \]
2. \[ \begin{align*} P_0 =& \left< 2,\dfrac{\pi}{4}\right>\\ \mathbf{r}_0 =& 2\,\mathbf{i} +\dfrac{\pi}{4} \,\mathbf{j}\\ \mathbf{r}_n(t) =& \left( 2\,\mathbf{i} +\dfrac{\pi}{4} \,\mathbf{j} \right) + t\,\left( -4\sqrt{2} \,\mathbf{i} -4\sqrt{2} \,\mathbf{j} + 2 \,\mathbf{k}\right)\\ =& \left( 2-4\sqrt{2}t \right) \,\mathbf{i} + \left( \dfrac{\pi}{4}-4\sqrt{2}t \right) \,\mathbf{j} +2t \,\mathbf{k} \end{align*} \]
3. Se $u=2$, $v=\pi/4$, temos \[ \begin{array}{llcl} x=& 2\cos \dfrac{\pi}{4} &=& \sqrt{2}\\ y=& 2\sin \dfrac{\pi}{4} &=& \sqrt{2}\\ z =& 4-1 &=& 3 \end{array} \nonumber \] por tanto o ponto $\displaystyle P_0 = \left< 2,\dfrac{\pi}{4}\right>$ no espaço $(u,v)$, corresponde ao ponto $P_0 = \left< \sqrt{2},\, \sqrt{2},\, 3\right> $, no espaço $(x,y,z)$, assim a parametrização da reta que passa por esse ponto é \[ \mathbf{q}(t) = \left( x- \sqrt{2}\right) \,\mathbf{i} + \left( y- \sqrt{2}\right) \,\mathbf{j} + \left( z-3 \right) \,\mathbf{k} \nonumber \] de forma que a equação do plano tangente está dada por \[ \begin{align*} \mathbf{q}\cdot \mathbf{n} &= 0\\ \left[ \left( x- \sqrt{2}\right) \,\mathbf{i} + \left( y- \sqrt{2}\right) \,\mathbf{j} + \left( z-3 \right) \,\mathbf{k} \right]\cdot \left[ -4\sqrt{2} \,\mathbf{i} -4\sqrt{2} \,\mathbf{j} + 2 \,\mathbf{k} \right] &=0\\ \left( x- \sqrt{2} \right) \left( -4\sqrt{2} \right) + \left( y- \sqrt{2} \right) \left( -4\sqrt{2} \right) + \left( z-3 \right) \left( 2 \right)&=0\\ 4\sqrt{2}(x+y)+z &= 5 \end{align*} \]

Exemplo 03

Determine o plano tangente à superfície $S$ dada por \[ x^2+y^2+z^2=4 \nonumber \] nos pontos a) $P=\left( 1,1,\sqrt{2} \right)$ e b) $P=\left( 0,0,2\right) $
SOL.

Exemplo 04

Determinar o campo vetorial normal unitário da esfera $x^2+y^2+z^2=a^2$ e represente graficamente.
SOL.

Exemplo

Mostre que o toro, o qual tem a representação vetorial \[ \mathbf{r}(u,v) = \left( a+b\cos\,v \right)\,\cos\,u \,\mathbf{i} + \left( a+b\cos\,v \right)\,\sin\,u \,\mathbf{j} + b\sin\,v \,\mathbf{k} \nonumber \] onde $a > b > 0$, é uma superfície suave
SOL.
\[ \begin{align*} \mathbf{T}_u \left(u_0,v_0 \right)&=\left( a+b\cos\,v_0 \right)\,\sin\,u_0\,\mathbf{i} + \left( a+b\cos\,v_0 \right)\,\cos\,u_0 \,\mathbf{j}\\ \mathbf{T}_v \left(u_0,v_0 \right)&= -b\sin\,v_0\cos\,u_0\,\mathbf{i} -b\sin\,v_0\sin\,u_0 \,\mathbf{j} + b\,\cos\,v_0 \,\mathbf{k}\\ \mathbf{T}_u \times \mathbf{T}_v &= \left( a+b\cos v_0 \right)b\cos v_0 \cos u_0 \,\mathbf{i} + \left( a+b\cos v_0 \right)b\cos v_0 \sin u_0\,\mathbf{j} + \left( a+b\cos v_0 \right)b\sin v_0 \,\mathbf{k}\\ &= \left( a+b\cos v_0 \right)b\,\left[ \cos v_0 \cos u_0 \,\mathbf{i} + \cos v_0 \sin u_0\,\mathbf{j} + \sin v_0 \,\mathbf{k} \right] \end{align*} \] como $a > b > 0$, o termo $b\left( a+b\cos v_0 \right)$ nunca é zero, além disso o seno e o cosseno nunca são simultaneamente zero, dessa forma o toro é uma superfície suave.

Exemplo 02

Indique se o cone, $z^2=x^2 + y^2$, é uma superfície suave.
SOL.
As equações paramétricas desse cone são \[ \begin{align*} x &= u\cos v\\ y &= u\sin v\\ z &= u \end{align*} \] de onde \[ \begin{align*} \mathbf{T}_u &= \cos u\,\mathbf{i} + \sin u \,\mathbf{j} + \,\mathbf{k}\\ \mathbf{T}_v &= -u\sin v\,\mathbf{i} + u\cos v \,\mathbf{j}\\ \mathbf{T}_u \times \mathbf{T}_v &= -u\cos v\,\mathbf{i} - u\sin v \,\mathbf{j} + u \,\mathbf{k} \end{align*} \] note que $\mathbf{T}_u \times \mathbf{T}_v=\mathbf{0}$ quando (e somente quando) $u=0$. O cone não é suave no vértice.

Exemplo 02

SOL.

Exemplo 02

Calcule o vetor normal da esfera parametrizada segundo a parametrização (coordenadas esféricas), no ponto $u=1/2$, $v=\pi/2$: \[ \begin{align*} x =& r \cos \,u\;\sin\, v\\ y =& r \sin \,u\;\sin\, v\\ z =& r \cos\, v \end{align*} \]

SOL.
\[ \begin{align*} \mathbf{T}_u &= r\cos u\sin v \,\mathbf{i} + r\sin u\sin v \,\mathbf{j} + \\ \mathbf{T}_v &=-u\sin v\,\mathbf{i} + u\cos v \,\mathbf{j} + \,\mathbf{k}\\ \mathbf{T}_u \times \mathbf{T}_v &= \end{align*} \]