Exemplo 01

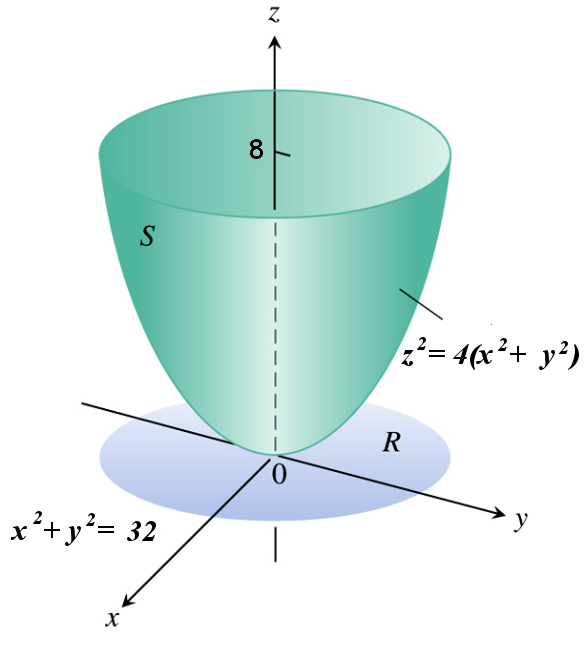
Seja o paraboloide $\displaystyle z=2\left( x^2 + y^2 \right)$, abaixo de $z=8$, parametrize e calcule sua área a partir dessa parametrização.
SOL.
O Paraboloide é uma superfície de revolução a qual rota em torno do eixo $z$, por tanto uma parametrização adequada para ele é da forma \[ \begin{align*} x =& f(u)\sin\,v\\ y =& f(u)\cos\,v\\ z =& f(u) \end{align*} \] como $z=2x^2$, quando $y=0$, vamos escolher $z=2u^2$, dessa forma \[ \begin{align*} x =& u\sin\,v\\ y =& u\cos\,v\\ z =& 2u^2 \end{align*} \] onde $0\leq v \leq 2\pi$ e \[ \begin{array}{ccccc} 0 & \leq & z & \leq & 8\\ 0 & \leq & 2u^2 & \leq & 8\\ 0 & \leq & u^2 & \leq & 4\\ 0 & \leq & u & \leq & 2 \end{array} \nonumber \] O vetor normal está dado por \[ \begin{align*} \mathbf{n} =& \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & \frac{\partial z}{\partial u}\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & \frac{\partial z}{\partial v} \end{vmatrix}\\ =&\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \sin v & \cos v & 4u\\ -u\cos v & u\sin v & 0 \end{vmatrix}\\ =& -4u^2\cos v \,\mathbf{i} + 4u^2\sin v \,\mathbf{j} + u \left( \sin^2 v + \cos^2 v\right) \,\mathbf{k}\\ =& -4u^2\cos v \,\mathbf{i} + 4u^2\sin v \,\mathbf{j} + u \,\mathbf{k}\\ \left| \, \mathbf{n} \, \right| =& \sqrt{16u^4\left( \sin^2 v + \cos^2 v \right) + u^2\;\;}\\ =& u\sqrt{16u^2 + 1\;\;} \end{align*} \] O diferencial de área é \[ d\sigma = u\sqrt{16u^2 + 1\;\;}du\,dv \nonumber \] assim a área está dada por \[ \begin{align*} A_S =& \int_0^{2\pi} \int_0^2 u\sqrt{16u^2 + 1\;\;}du\,dv \end{align*} \] fazendo \[ \begin{align*} \omega =& 16u^2 + 1\\ \omega =& 32u\,du \end{align*} \] e os limites de integração mudam para \[ \begin{array}{cccc} \text{Se u } = 0 & \Rightarrow & \omega =& 1\\ \text{Se u } = 2 & \Rightarrow & \omega =& 65 \end{array} \nonumber \] assim \[ \begin{align*} A_S =& \int_0^{2\pi} \int_1^{65} \dfrac{1}{32}\sqrt{\omega}\,d\omega\,dv\\ =& \dfrac{1}{48}\int_0^{2\pi} \left( 65 ^{3/2} - 1^{3/2} \right) dv\\ =& \dfrac{65\sqrt{65}-1}{24}\pi \end{align*} \]

Utilizando a representação explícita

Como \[ z=2\left( x^2 + y^2 \right) \nonumber \] resulta obvio que nosso elemento de integração está dado por \[ d\sigma = \sqrt{1 + \left( \dfrac{\partial z}{\partial x} \right)^2 + \left(\dfrac{\partial z}{\partial y} \right)^2\;}\, dx\,dy \nonumber \] o qual significa que nos transladamos nossa integral da superfície para o plano $xy$. No plano $xy$ a projeção da superfície do é um círculo o qual está definido pela circunferência delineada pela borda superior do paraboloide quando $z=8$, isto é \[ x^2+y^2\leq 4 \nonumber \] dessa forma \[ A = \iint_{x^2+y^2\leq 4}\,d\sigma \nonumber \] dessa forma \[ \begin{align*} \dfrac{\partial z}{\partial x} =& 4x\\ \dfrac{\partial z}{\partial y} =& 4y \end{align*} \] de onde \[ \begin{align*} A =& \iint_{x^2+y^2\leq 4} \sqrt{1 + 16x^2+16y^2\,}\,dx\,dy\\ =& \iint_{x^2+y^2\leq 4} 2\,dx\,dy \end{align*} \] utilizando coordenadas polares $dx\,dy = r\,dr\,d\theta$, \[ \begin{align*} A =& \int_0^2 \int_0^{2\pi} \sqrt{1+16r\;}r\,d\theta\,dr\\ =& \dfrac{65\sqrt{65}-1}{24}\pi \end{align*} \]

Utilizando a representação implícita

A função anterior fica expressada de forma implícita quando \[ 2\left( x^2 + y^2 \right)-z=0 \nonumber \] de onde \[ \begin{align*} \vec{\nabla}\,f =& 4x\,\mathbf{i} + 4y \,\mathbf{j} + \,\mathbf{k}\\ \left| \, \vec{\nabla}\,f \, \right| =& \sqrt{1 + 16x^2+16y^2\,} \end{align*} \] Como a projeção mais obvia é o plano $xy$ temos que \[ \vec{\nabla}\,f \cdot \mathbf{k} = 1 \nonumber \] por tanto \[ \begin{align*} A =& \iint_{x^2+y^2\leq 4} \sqrt{1 + 16x^2+16y^2\,}\,dx\,dy\\ =& \iint_{x^2+y^2\leq 4} 2\,dx\,dy \end{align*} \] utilizando coordenadas polares $dx\,dy = r\,dr\,d\theta$, \[ \begin{align*} A =& \int_0^2 \int_0^{2\pi} \sqrt{1+16r\;}r\,d\theta\,dr\\ =& \dfrac{65\sqrt{65}-1}{24}\pi \end{align*} \]

Exemplo 02

Seja $S$ definida por $\displaystyle z=\sqrt{a^2-x^2-y^2}$ (semi esfera superior), parametrize e calcule sua área a partir dessa parametrização.
SOL.
Seguindo a parametrização da Diva, teremos \[ \begin{align*} x =& a\cos\,u\,\cos\,v\\ y =& a\sin\,u\,\cos\,v\\ z =& a\sin\,v \end{align*} \] com limites de integração são $0\leq u \leq 2\pi$ e $0 \leq v \leq \pi/2\pi$. Utilizando a notação do Jacobiano, o elemento de superfície está dado por \[ \begin{align*} d \sigma =& \sqrt{\left( \, \frac{\partial \left(\, y,z\,\right)}{\partial \left(\, u,v\,\right)} \, \right)^2 + \left( \, \frac{\partial \left(\, z,x\,\right)}{\partial \left(\, u,v\,\right)} \, \right)^2 + \left( \, \frac{\partial \left(\, x,y \,\right)}{\partial \left(\, u,v\,\right)} \, \right)^2\;\,\,}\,\,\,du\,dv\\ \frac{\partial \left(\, y,z\,\right)}{\partial \left(\, u,v\,\right)} =& \frac{\partial y}{\partial u}\, \frac{\partial z}{\partial v} - \frac{\partial y}{\partial v}\, \frac{\partial z}{\partial u}\\ =& \left( a\cos\,u\,\cos\,v \right)\left( a\cos\,v \right) -0\\ =& a^2\cos u\,\cos^2 v \\ \frac{\partial \left(\, z,x\,\right)}{\partial \left(\, u,v\,\right)} =& \frac{\partial z}{\partial u}\, \frac{\partial x}{\partial v} - \frac{\partial z}{\partial v}\, \frac{\partial x}{\partial u}\\ =& 0 - \left( a\cos\,v \right)\left( -a\sin\,u\,\cos\,v \right)\\ =& a^2\sin\, u\,\cos^2v \\ \frac{\partial \left(\, x,y\,\right)}{\partial \left(\, u,v\,\right)} =& \frac{\partial x}{\partial u}\, \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v}\, \frac{\partial y}{\partial u}\\ =& \left( -a\sin\,u\,\cos\,v \right)\left( -a\sin\,u\,\sin\,v \right) - \left( -a\cos\,u\,\sin\,v\right)\left( a\cos\,u\,\cos\,v \right)\\ =& a^2\sin^2 u\,\sin\,v\,\cos\,v + a^2\cos^2 u\,\sin\,v\,\cos\,v\\ =& a^2\sin\,v\,\cos\,v\\ d \sigma =& \sqrt{a^4\cos^2 u\,\cos^4 v + a^4\sin^2 u\,\cos^4v + a^4\sin^2 v\,\cos^2v\;\;\;\;}\\ =& a^2\sqrt{ \left( \cos^2 u + \sin^2 u \right)\,\cos^4 v + \sin^2 v\,\cos^2v \;\;\;\;}\\ =& a^2\sqrt{ \cos^2 v\left( \cos^2 v + \sin^2 v \right) \;\;\;\;}\\ =& a^2\cos\, v\\ A_s =& a^2\int_0^{2\pi} \int_0^{\pi/2}\cos\, v\,dv\,du\\ =& a^2 \int_0^{2\pi} \sin\, v \bigg|_0^{\pi/2}\,du\\ =& a^2 \int_0^{2\pi} du\\ =& 2\pi\,a^2 \end{align*} \]

Exemplo 03

Dado enunciado do exemplo 01, considere a função de forma definida explicitamente e calcule sua superfície
SOL.
Primeiro escrevemos a equação de forma implícita \[ F(x,y,z)=x^2 + y^2 - \dfrac{z}{2} = 0 \nonumber \] quando $z=8$ a projeção no plano $xy$ a figura que se forma é uma circunferência dada pela equação \[ x^2 + y^2 = 4 \nonumber \] e o vetor perpendicular a essa superfície é $\mathbf{p}=\mathbf{k}$

Calculando o gradiente de $F(x,y,z)$ \[ \begin{align*} \vec{\nabla}F(x,y,z) =& 2x\,\mathbf{i} + 2y \,\mathbf{j} -\dfrac{1}{2} \,\mathbf{k}\\ \left| \, \vec{\nabla}F(x,y,z) \, \right| =& \sqrt{4x^2+4y^2+\dfrac{1}{4}\;\;}\\ \vec{\nabla}F\cdot\mathbf{k} =& \dfrac{1}{2}\\ \dfrac{\left| \, \vec{\nabla}F \, \right|}{\vec{\nabla}F\cdot\mathbf{k}} =& \sqrt{16x^2+16y^2+1\;\;} \end{align*} \] como a superfície está projetada no plano $xy$ \[ d\sigma = \sqrt{16x^2+16y^2+1\;\;}dx\,dy \nonumber \] Assim \[ A_S = \iint_R\sqrt{16x^2+16y^2+1\;\;}dx\,dy \nonumber \] passando para coordenadas polares \[ A_S = \int_0^{2\pi}\int_0^{2}\sqrt{16r^2+1\;\;}rdr\,d\theta \nonumber \] note que essa integral é a mesma do problema 1 \[ A_S = \dfrac{65\sqrt{65}-1}{24}\pi \nonumber \]

Exemplo 04

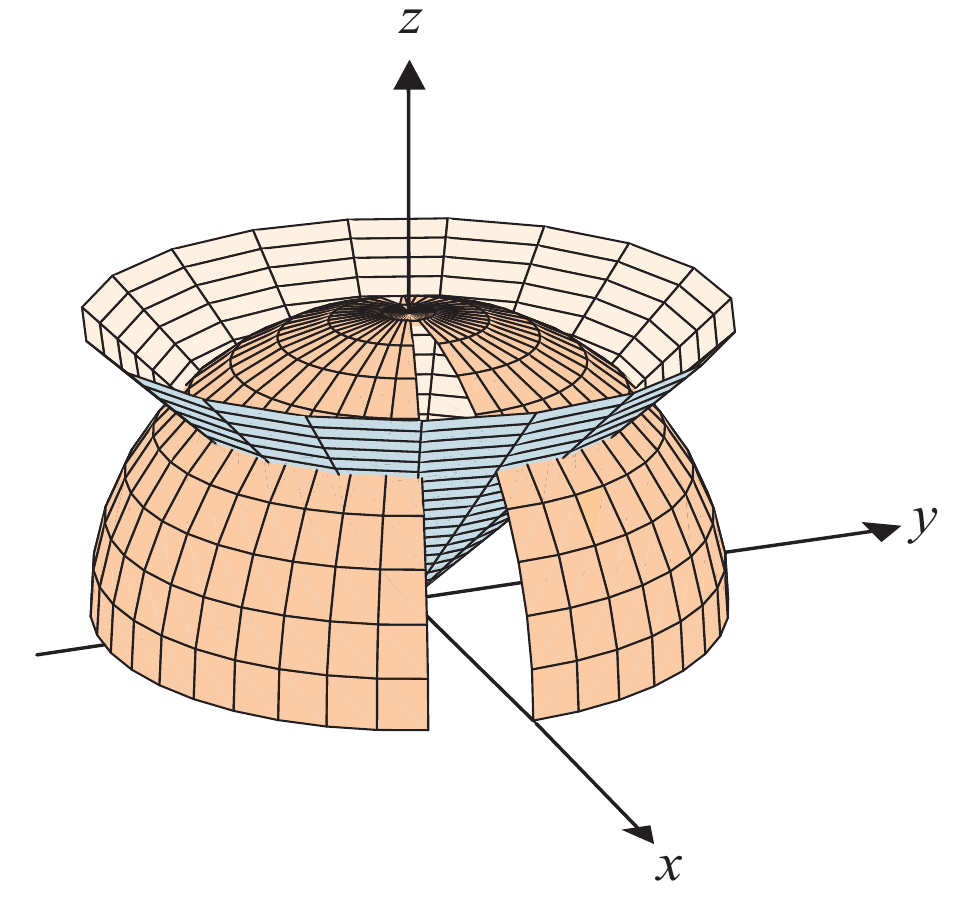
Encontre a área da esfera $x^2+y^2+z^2=2$ que está delimitada pelo cone $z=\sqrt{x^2+y^2}$
SOL.
Na figura embaixo se mostra uma figura que representando a situação descirta no problema

É obvio que a projeção no plao $xy$ será uma circunferência, por tanto $\mathbb{p}=\mathbb{k}$, assim \[ \begin{align*} \vec{\nabla}F =& \vec{\nabla}\left( x^2+y^2+z^2 \right)\\ =& 2x \,\mathbf{i} +2y \,\mathbf{j} + 2z \,\mathbf{k}\\ \vec{\nabla}F\cdot \mathbb{k} =& 2z\\ \left| \, \vec{\nabla}F \, \right| =& 2\sqrt{x^2+y^2+z^2}\\ =& 2\sqrt{2}\\ \dfrac{\left| \, \vec{\nabla}F \, \right|}{\vec{\nabla}F\cdot\mathbf{k}} =& \dfrac{2\sqrt{2}}{2z}\\ =&\dfrac{\sqrt{2}}{z}\\ =&\dfrac{\sqrt{2}}{\sqrt{2-x^2-y^2}}\\ \end{align*} \] de onde \[ A_S = \iint_R \dfrac{\sqrt{2}}{\sqrt{2-x^2-y^2}}\,dx\,dy \nonumber \] Como o objetivo do cone é limitar à circunferência, devemos encontrar o valor dos pontos onde as duas curvas se interceptam \[ \begin{align*} x^2+y^2+z^2 =& 2\\ x^2+y^2+\left( \sqrt{x^2+y^2} \right)^2 =& 2\\ 2\left( x^2+y^2 \right) =&2\\ x^2+y^2 =& 1 \end{align*} \] assim, a curva de interceção é uma circunferência de raio $1$, a que corresponde à área de $R$, ou seja \[ A_S = \iint_{x^2+y^2\leq 1} \dfrac{\sqrt{2}}{\sqrt{2-x^2-y^2}}\,dx\,dy \nonumber \] passando para coordenadas polares \[ A_S = \int_0^{2\pi} \int_0^2 \dfrac{\sqrt{2}}{\sqrt{2-r^2}}\,r\,dr\,d\theta \nonumber \] usando $w=2-r^2 \Rightarrow dw=-2r\,dr$ e $r=0\Rightarrow w=2$, $r=1\Rightarrow w=1$, assim \[ \begin{align*} A_S =& -\int_0^{2\pi} \int_2^1 \dfrac{\sqrt{2}}{\sqrt{w}}\,dw\,d\theta\\ =& -\int_0^{2\pi}\dfrac{2\sqrt{2}}{2}\sqrt{w}\,\Big|_2^1\,d\theta\\ =& \sqrt{2}\int_0^{2\pi}\left( \sqrt{2}-1 \right) \, d\theta\\ =& 2\pi \left( 2-\sqrt{2} \right) \end{align*} \]

Exemplo 05

Seja $S$ a superfície de uma bola de futbol americano formada ao gira a curva $x=\cos\,z$, $y=0$, $\pi/2\leq z \leq \pi/2$ ao redor do eixo $z$. Encontre uma parametrização e calcule a área da superfície.
SOL.
Primeiramente devemos parametrizar a superfície de revolução: \[ \begin{cases} x =& \cos u\, \cos v\\ y =& \cos u\, \sin v\\ z =& u \end{cases} \nonumber \] onde $0\leq u < \frac{\pi}{2}$ e $0\leq v \leq 2\pi$, o qual resulta em

Exemplo 05

Se a parametrização de um helicoide está dada por \[ x = u\cos\,v\;\;\;\;\;\;y=u\sin\,v\;\;\;\;\;\;z=v \nonumber \] onde $0 \leq u\leq 1$ e $0\leq v \leq 2\pi$, calcule a área da sua superfície.

Exemplo 06

Encontrar a área de um toro o qual é parametrizada pela equação \[ \mathbf{r}(u,v) = \left( 2+\cos u \right) \cos v+ \,\mathbf{i} + \left( 2+\cos u \right) \sin v\,\mathbf{j} +\sin u \,\mathbf{k} \nonumber \] onde $0\leq u \leq 2\pi$ e $0\leq v \leq 2\pi$.

Exemplo 07

Calcule a área da cúpula obtida a partir da interseção da esfera $x^2+y^2+z^2=2$ e o cilindro $x^2+y^2=1$.

Exemplo 08

Calcule a área da parte do cilindro $x^2+ y^2=2ay$ que está dentro da esfera $x^2+y^2+z^2=4ay$
SOL.
O cilindro $x^2+y^2=2ay$ interseta à esfere $x^2+y^2+z^2=4a^2$ no cilindro parabólico \[ \begin{align*} \left( x^2+y^2 \right)+z^2=&4a^2\\ 2ay+z^2=&4a^2 \end{align*} \] O elemento de área do cilindro $F(x,y,z) = x^2+y^2-2ay=0$ projetado contra o plano $yz$ está dado por \[ \begin{align*} d\sigma =& \dfrac{\left| \, \vec{\nabla}F \, \right|}{\left| \, \, \vec{\nabla}F\cdot \mathbf{p}\right|}\,dy\,dz\\ =& \dfrac{\left| \, 2x\,\mathbf{i} + 2\left( y-a \right) \,\mathbf{j} \, \right|}{\left| \, \left[ 2x\,\mathbf{i} + 2\left( y-a \right) \,\mathbf{j} \right]\cdot \mathbf{i} \, \right|}\,dy\,dz\\ =& \dfrac{\sqrt{x^2+\left( y-a \right)^2}}{x}\,dy\,dz\\ =& \sqrt{1-\dfrac{\left( y-a \right)^2}{x}} \end{align*} \] como \[ \begin{align*} x^2+y^2=&2ay\\ x^2=&2ay-y^2 \end{align*} \] dessa forma \[ \begin{align*} d\sigma =& \sqrt{1+\dfrac{y^2-2ay+a^2}{2ay-y^2}\,\,}\\ =& \sqrt{\dfrac{2ay-y^2+y^2-2ay+a^2}{2ay-y^2}\,\,}\\ =& \sqrt{\dfrac{a^2}{2ay-y^2}\,\,} \end{align*} \] A área que desejamos é quatro vezes a área mostrada na figura

e os limites de integração estão dados por \[ \begin{array}{ccccl} 0 & \leq & y & \leq & 2a\\ 0 & \leq & z & \leq & \sqrt{4a^2-2ay\,\,} \end{array} \nonumber \] este último sendo o cilindro parabólico, assim \[ \begin{align*} A_S =& 4\int_0^{2a}\int_0^\sqrt{4a^2-2ay\,\,} \dfrac{a}{\sqrt{2ay-y^2}\,\,}\,dz\,dy\\ =& 4\int_0^{2a} \dfrac{a\sqrt{4a^2-2ay\,\,}}{\sqrt{2ay-y^2}\,\,}\,dy\\ =& 4\int_0^{2a} \dfrac{a\sqrt{2a\left( 2a-y \right) \,\,}}{\sqrt{y\left( 2a-y \right) }\,\,}\,dy\\ =& 4a\sqrt{2a\,\,}\int_0^{2a} \dfrac{dy}{\sqrt{y\,\,}}\\ =& 4\sqrt{2a\,\,} \left( 2\sqrt{y\,\,} \right)\Bigg|_0^{2a}\\ =& 16a^2 \end{align*} \]