Exemplo 01
Calcule o fluxo do campo vetorial
\[
\mathbf{F}(x,y,z) =x \,\mathbf{i} + y \,\mathbf{j} + z \,\mathbf{k}
\nonumber
\]
através da superfície de uma esfera de raio $a$ utilize coordenadas esférica para representar a superfície (parametrização do resto do mundo)
SOL.
Por definição a integral de fluxo
\[
\Phi_{S}=\iint_{R}\mathbf{F}\cdot d\vec{\sigma}
\nonumber
\]
onde
\[
d\vec{\sigma}=\mathbf{n}\, dudv
\nonumber
\]
com
\[
\mathbf{n}=\mathbf{T}_{u}\times\mathbf{T}_{v}
\nonumber
\]
e
\[
\mathbf{T}_{u}=\dfrac{\partial\mathbf{r}}{\partial u}\qquad\text{e}\qquad\mathbf{T}_{v}=\dfrac{\partial\mathbf{r}}{\partial v}
\nonumber
\]
Uma outra alternativa a essa abordagem é utilizar o Jacobiano
\[
\mathbf{n}=\dfrac{\partial\left(y,z\right)}{\partial\left(u,v\right)}\,\mathbf{i}+\dfrac{\partial\left(z,x\right)}{\partial\left(u,v\right)}\,\mathbf{j}+\dfrac{\partial\left(x,y\right)}{\partial\left(u,v\right)}\,\mathbf{k}
\nonumber
\]
sendo que $x,\, y,\, z$ são as coordenadas do vetor $\mathbf{r}$
que é a parametrização da superfície por onde o campo vai fluir, que
para o caso da esfera, em coordenadas esféricas, é
\[
\mathbf{r}(u,v)=a\,\sin v\,\cos u\,\mathbf{i}+a\,\sin v\,\sin u\,\mathbf{j}+a\cos v\,\mathbf{k},\qquad0\leq u\leq2\pi,\:0\leq v\leq\pi
\nonumber
\]
de forma que
\[
\begin{align*}
\mathbf{n}= & \left[\dfrac{\partial y}{\partial u}\dfrac{\partial z}{\partial v}-\dfrac{\partial z}{\partial u}\dfrac{\partial y}{\partial v}\right]\,\mathbf{i}+\left[\dfrac{\partial z}{\partial u}\dfrac{\partial x}{\partial v}-\dfrac{\partial x}{\partial u}\dfrac{\partial z}{\partial v}\right]\,\mathbf{j}+\left[\dfrac{\partial x}{\partial u}\dfrac{\partial y}{\partial v}-\dfrac{\partial y}{\partial u}\dfrac{\partial x}{\partial v}\right]\,\mathbf{k}\\
= & \left[\left(a\sin v\cos u\right)\left(-a\sin v\right)-\left(0\right)\left(a\cos v\sin u\right)\right]\,\mathbf{i}+\\
& \left[\left(0\right)\left(a\cos v\right)-\left(-a\sin v\sin u\right)\left(-a\sin v\right)\right]\,\mathbf{j}+\\
& \left[\left(-a\sin v\sin u\right)\left(a\cos v\sin u\right)-\left(a\sin v\cos u\right)\left(a\cos v\cos u\right)\right]\,\mathbf{k}\\
= & -\left(a^{2}\sin^{2}v\cos u\right)\,\mathbf{i}-\left(a^{2}\sin^{2}v\sin u\right)\,\mathbf{j}-\\
& \left(a^{2}\sin v\cos v\sin^{2}u+a\sin v\cos v\cos^{2}u\right)\,\mathbf{k}\\
= & -\left(a^{2}\sin^{2}v\cos u\right)\,\mathbf{i}-\left(a^{2}\sin^{2}v\sin u\right)\,\mathbf{j}-\\
& a^{2}\sin v\cos v\left(\sin^{2}u+\cos^{2}u\right)\,\mathbf{k}\\
= & -\left(a^{2}\sin^{2}v\cos u\right)\,\mathbf{i}-\left(a^{2}\sin^{2}v\sin u\right)\,\mathbf{j}-a^{2}\sin v\cos v\,\mathbf{k}\\
= & -a\sin v\left[a\,\sin v\,\cos u\,\mathbf{i}+a\,\sin v\,\sin u\,\mathbf{j}+a\cos v\,\mathbf{k}\right]\\
= & -a\sin v\,\mathbf{r}
\end{align*}
\]
Note que o vetor $\mathbf{n}$ aponta para dentro da esfera já que
$\sin v\geq0$ no intervalo $0\leq v\leq \pi$ de forma que $\displaystyle \mathbf{n}$ sempre aponta na direção de $\displaystyle -\mathbf{r}$ ou seja, para dentro da esfera. Devido a que desejamos trabalhar com a orientação positiva redefinimos nosso vetor normal para
\[
\mathbf{n}=a\sin v\,\mathbf{r}
\nonumber
\]
Escrevendo o campo $\mathbf{F}$ em termos de $(u,v)$:
\[
\begin{align*}
\mathbf{F}(u,v)= & a\,\sin v\,\cos u\,\mathbf{i}+a\,\sin v\,\sin u\,\mathbf{j}+a\cos v\,\mathbf{k}\\
= & \mathbf{r}
\end{align*}
\]
de onde o elemento de fluxo está dado por
\[
\begin{align*}
\mathbf{F}\cdot\mathbf{n}= & \left(a\sin v\,\mathbf{r}\right)\cdot\mathbf{r}\\
= & a\sin v
\end{align*}
\]
dessa forma a integral de superfície do campo vetorial será
\[
\begin{align*}
\Phi_{S}= & \iint_{R}\mathbf{F}\cdot d\vec{\sigma}\\
= & \int_{0}^{\pi}\int_{0}^{2\pi}a\sin v\, du\, dv\\
= & 2\pi a\int_{0}^{\pi}\sin v\, dv\\
= & -2\pi a\left(\cos\pi-\cos0\right)\\
= & 4\pi a
\end{align*}
\]
Exemplo 02
Repita o problema anterior considerando a parametrização da Diva.
SOL.
No caso da parametrização da diva temos
\[
\mathbf{r}(u,v)=a\,\cos v\,\cos u\,\mathbf{i}+a\,\cos v\,\sin u\,\mathbf{j}+a\sin v\,\mathbf{k},\qquad0\leq u\leq2\pi,\:0\leq v\leq\pi
\nonumber
\]
de onde
\[
\begin{align*}
\mathbf{n}= & \left[\dfrac{\partial y}{\partial u}\dfrac{\partial z}{\partial v}-\dfrac{\partial z}{\partial u}\dfrac{\partial y}{\partial v}\right]\,\mathbf{i}+\left[\dfrac{\partial z}{\partial u}\dfrac{\partial x}{\partial v}-\dfrac{\partial x}{\partial u}\dfrac{\partial z}{\partial v}\right]\,\mathbf{j}+\left[\dfrac{\partial x}{\partial u}\dfrac{\partial y}{\partial v}-\dfrac{\partial y}{\partial u}\dfrac{\partial x}{\partial v}\right]\,\mathbf{k}\\
= & \left[\left(a\cos v\cos u\right)\left(a\cos v\right)-\left(0\right)\left(-a\sin v\sin u\right)\right]\,\mathbf{i}+\\
& \left[\left(0\right)\left(a\cos v\right)-\left(-a\cos v\sin u\right)\left(a\cos v\right)\right]\,\mathbf{j}+\\
& \left[\left(-a\cos v\sin u\right)\left(-a\sin v\sin u\right)-\left(a\cos v\cos u\right)\left(-a\sin v\cos u\right)\right]\,\mathbf{k}\\
=& a^2\cos^2 v\cos u\,\mathbf{i} + a^2\cos^2 v\sin u\,\mathbf{j} + a^2\cos v \sin v \left( \sin^2 u + \cos^2 u\right) \,\mathbf{k}\\
=& a^2\cos^2 v\cos u\,\mathbf{i} + a^2\cos^2 v\sin u\,\mathbf{j} + a^2\cos v \sin v\,\mathbf{k}\\
=& a^2\cos v\left( \cos v\,\cos u\,\mathbf{i}+\cos v\,\sin u\,\mathbf{j}+\sin v\,\mathbf{k} \right)\\
=& a^2\cos v\, \mathbf{r}
\end{align*}
\]
Note que o vetor $\mathbf{n}$ aponta para dentro da esfera já que
$\cos v\geq0$ no intervalo $-\dfrac{\pi}{2} \leq v\leq\dfrac{\pi}{2}$ de forma que $\displaystyle \mathbf{n}$ sempre aponta na direção de $\displaystyle \mathbf{r}$ ou seja, para fora da esfera.
Escrevendo o campo $\mathbf{F}$ em termos de $(u,v)$:
\[
\begin{align*}
\mathbf{F}(u,v)= & a\,\cos v\,\cos u\,\mathbf{i}+a\,\cos v\,\sin u\,\mathbf{j}+a\sin v\,\mathbf{k}\\
= & \mathbf{r}
\end{align*}
\]
de onde o elemento de fluxo está dado por
\[
\begin{align*}
\mathbf{F}\cdot\mathbf{n}= & \left(a^2\cos v\,\mathbf{r}\right)\cdot\mathbf{r}\\
= & a^2\cos v
\end{align*}
\]
dessa forma a integral de superfície do campo vetorial será
\[
\begin{align*}
\Phi_{S}= & \iint_{R}\mathbf{F}\cdot d\vec{\sigma}\\
= & \int_{-\pi/2}^{\pi/2}\int_{0}^{2\pi}a^2\cos v\, du\, dv\\
= & 2\pi a^2\int_{\pi/2}^{\pi}\cos v\, dv\\
= & 2\pi a^2\left[\sin\dfrac{\pi}{2}-\sin \left( -\dfrac{\pi}{2} \right)\right]\\
= & 4\pi a^2
\end{align*}
\]
Exemplo 03
Calcule o fluxo de $\mathbf{F}(x,y,z) =x\,\mathbf{k}$, se a superfície está representada pela parametrização \[ \mathbf{r}(u,v) = u^2\,\mathbf{i} + v \,\mathbf{j} + \left( u^3-v^2\right) \,\mathbf{k} \nonumber \] orientada para cima.
SOL.
Como temos uma superfície parametrizada o nosso elemento de área é definido da seguinte forma
\[
\begin{align*}
d\vec{\sigma} =& \mathbf{n}\,da\\
=&\left( \mathbf{T}_{u}\times\mathbf{T}_{v} \right) \,du\,dv
\end{align*}
\]
dessa forma calculamos o campo normal
\[
\begin{align*}
\mathbf{n}= & \left[\dfrac{\partial y}{\partial u}\dfrac{\partial z}{\partial v}-\dfrac{\partial z}{\partial u}\dfrac{\partial y}{\partial v}\right]\,\mathbf{i}+\left[\dfrac{\partial z}{\partial u}\dfrac{\partial x}{\partial v}-\dfrac{\partial x}{\partial u}\dfrac{\partial z}{\partial v}\right]\,\mathbf{j}+\left[\dfrac{\partial x}{\partial u}\dfrac{\partial y}{\partial v}-\dfrac{\partial y}{\partial u}\dfrac{\partial x}{\partial v}\right]\,\mathbf{k}\\
=& \left[ \left( 0 \right)\left( -2v \right) - \left( 3u^2 \right)\left( 1 \right) \right]\,\mathbf{i} + \left[ \left( 3u^2 \right)\left( 0 \right) - \left( 2u \right)\left( -2v \right) \right]\,\mathbf{j} +\\
&\left[ \left( 2u \right)\left( 1 \right) - \left( 0 \right)\left( 0 \right) \right]\,\mathbf{k}\\
=& -3u^2\,\mathbf{i} +4u^2v \,\mathbf{j} +2u \,\mathbf{k}
\end{align*}
\]
Escrevendo o campo em termos dos vetores $(u,\,v)$:
\[
\mathbf{F}(u,v) = u^2\,\mathbf{k}
\nonumber
\]
de forma que
\[
\mathbf{F}\cdot \mathbf{n} = 2u^3
\nonumber
\]
por tanto
\[
\begin{align*}
\Phi =& \iint_S \mathbf{F}\cdot \mathbf{n}\, du\,dv\\
=& 2\int_0^1 \int_0^1 u^3 dv\,du\\
=& 2\int_0^1 u^3 du\\
=& \dfrac{1}{2}
\end{align*}
\]
Exemplo 04
Calcular o fluxo do campo $\displaystyle \mathbf{F}(x,y,z)= z \,\mathbf{i} + x\,\mathbf{j} + \mathbf{k}$ através do hemisfério da esfera $\displaystyle x^2 + y^2 + z^2 = 1$, orientada com vetores para fora.
SOL.
A parametrização desse hemisfério está dada por
\[
\mathbf{r}(u,v)=a\,\sin v\,\cos u\,\mathbf{i}+a\,\sin v\,\sin u\,\mathbf{j}+a\cos v\,\mathbf{k},\qquad0\leq u\leq2\pi,\:0\leq v\leq\pi
\nonumber
\]
com $\displaystyle 0 \leq v \leq \dfrac{\pi}{2}$ e $\displaystyle 0 \leq u \leq 2\pi$. Como vimos no exemplo 1 o vetor normal está dado por
\[
\mathbf{n}=a\sin v\left[a\,\sin v\,\cos u\,\mathbf{i}+a\,\sin v\,\sin u\,\mathbf{j}+a\cos v\,\mathbf{k}\right]
\nonumber
\]
Reescrevendo o campo em termos de $(u,v)$:
\[
\mathbf{F} = a\cos v \,\mathbf{i} + a\,\sin v\,\cos u \,\mathbf{j} + \mathbf{k}
\nonumber
\]
de onde
\[
\mathbf{F}\cdot \mathbf{n} = a^2\,\sin^2 v\,\cos v\cos u + a^2\,\sin^3 v\,\sin u\, \cos u + a^2\sin v \,\cos v
\nonumber
\]
integrando
\[
\begin{align*}
\Phi =& \iint_S \mathbf{F}\cdot \mathbf{n}\, du\,dv\\
=& a^2\int_0^{\pi/2} \int_0^{2\pi} \left[\, \sin^2 v\,\cos v\cos u + \sin^3 v\,\sin u\, \cos u + \sin v \,\cos v \,\right] du\,dv\\
=& a^2\int_0^{\pi/2} \sin^2 v\,\cos v\, \cancelto{0,\;\text{função periodica}}{\int_0^{2\pi} \cos u\, du\,dv} +\\
& a^2\int_0^{\pi/2} \sin^3 v\, \int_0^{2\pi} \sin u\, \cos u \,du\,dv + a^2\int_0^{\pi/2} \sin v \,\cos v \, \int_0^{2\pi}du\,dv
\end{align*}
\]
utilizando a identidade trigonométrica
\[
\begin{align*}
\sin\,u\,\cos\,u=&\dfrac{1}{2}\left[ \sin\left( u-u \right) + \sin\left( u+u \right) \right]\\
=& \dfrac{1}{2}\sin\,2u
\end{align*}
\nonumber
\]
por tanto a II integral também é zero pois estamos integrando num período. Dessa forma o fluxo está dado por
\[
\begin{align*}
\Phi =& a^2\int_0^{\pi/2} \sin v \,\cos v \, \int_0^{2\pi}du\,dv\\
=& \pi\,\int_0^{\pi/2}\sin\,2u\,du\\
=& \dfrac{\pi}{2}\,\int_0^{pi}\sin\,w\,dw\\
=& -\dfrac{\pi}{2}\left(\cos\,\pi - \cos\,0 \right)\\
=&\pi
\end{align*}
\]
Exemplo 05
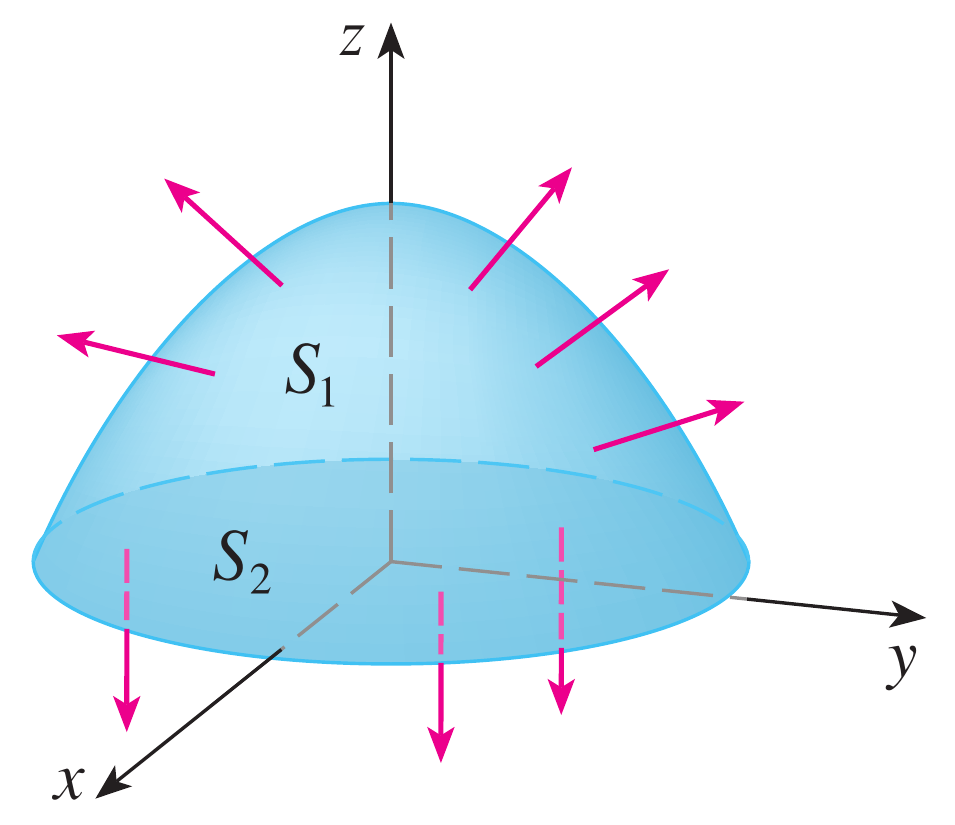
Calcule o fluxo do campo \[ \mathbf{F}(x,y,z) = y\,\mathbf{i} +x \,\mathbf{j} +z \,\mathbf{k} \nonumber \] e $S$ é a superfície externa da região sólida $E$ delimitada pelo paraboloide $z=1-x^2-y^2$ e o plano $z=0$
SOL.
A interseção do paraboloide $z=1-x^{2}-y^{2}$ com o plano $z=0$ está dado por
\[
\begin{align*}
1-x^{2}-y^{2} & =z\\
1-x^{2}-y^{2} & =0\\
x^{2}+y^{2} & =1
\end{align*}
\]
uma circunferência de raio $1$. Por tanto a nossa superfície é formada
na realidade por duas superfícies, o paraboloide acima de z=0 e o
círculo de raio 1 no plano $xy$, isto é
\[
\Phi=\iint_{S_{1}}\mathbf{F}\cdot d\vec{\sigma}+\iint_{S_{2}}\mathbf{F}\cdot d\vec{\sigma}
\nonumber
\]
Em ambos casos podemos pensar as superfícies definidas de forma implícita.
Analisemos primeiramente a superfície o fluxo através da superfície
$S_{1}$:
\[
\begin{align*}
f= & x^{2}+y^{2}+z-1\\
\vec{\nabla f}= & 2x\,\mathbf{i}+2y\,\mathbf{j}+\mathbf{k}\\
\vec{\nabla f}\cdot\mathbf{k}= & 1
\end{align*}
\]
\[
\begin{align*}
\mathbf{n}_{1}= & \pm\dfrac{\vec{\nabla f}}{\vec{\nabla f}\cdot\mathbf{k}}\\
= & 2x\,\mathbf{i}+2y\,\mathbf{j}+\mathbf{k}
\end{align*}
\]
onde foi escolhido o sinal positivo já que o fluxo será calculado
saindo da superfície. Escrevendo o campo em termos de $x,\, y$
\[
\begin{align*}
\mathbf{F}(x,y)= & y\,\mathbf{i}+x\,\mathbf{j}+\left(1-x^{2}-y^{2}\right)\,\mathbf{k}\\
\mathbf{F}\cdot\mathbf{n}= & 2xy+2xy+1-x^{2}-y^{2}\\
= & 1+4xy-x^{2}-y^{2}
\end{align*}
\]
Levando em consideração que a superfícies está projetada no plano
$xy$ numa região definida por $0\leq x^{2}+y^{2}\leq1$, temos que
o fluxo está dado por
\[
\begin{align*}
\Phi_{1}= & \iint_{S_{1}}\mathbf{F}\cdot d\vec{\sigma}\\
= & \iint_{0\leq x^{2}+y^{2}\leq1}\left(1+4xy-x^{2}-y^{2}\right)dx\, dy
\end{align*}
\]
passando para coordenadas polares e considerando
\[
\begin{align*}
\Phi_{1}= & \int_{0}^{2\pi}\int_{0}^{1}\left(1+4r^{2}\cos\theta\sin\theta-r^{2}\right)r\, dr\, d\theta\\
= & \int_{0}^{2\pi}\left(\dfrac{1}{2}+\cos\theta\sin\theta-\dfrac{1}{4}\right)d\theta\\
= & \dfrac{\pi}{2}+\int\sin2\theta\, d\theta\\
= & \dfrac{\pi}{2}
\end{align*}
\]
Para o caso da superfície $S_{2}$ temos
\[
\begin{align*}
f_{2}= & z\\
\vec{\nabla f}_{2}= & \mathbf{k}\\
\vec{\nabla f}_{2}\cdot \mathbf{k} =& 1\\
d\vec{\sigma} =& \dfrac{\vec{\nabla f}_{2}}{\left|\,\vec{\nabla f}_{2}\cdot \mathbf{k}\,\right|}dx\,dy\\
=&\mathbf{k}\,dx\,dy
\end{align*}
\]
dessa forma a integral está dada por
\[
\begin{align*}
\Phi = & \iint_{0 \leq x^2+y^2 \leq 1}\left(y\,\mathbf{i}+x\,\mathbf{j}+z\,\mathbf{k}\right)\cdot \left( \mathbf{k}\,dx\,dy\right)\\
\mathbf{F}\cdot\mathbf{n}= & \iint_{0 \leq x^2+y^2 \leq 1} z \,dx\,dy\\
= & -4xy
\end{align*}
\]
como o valor de $z$ no plano é zero, então o fluxo pela superfície é $\Phi_2=0$
dessa forma
\[
\begin{align*}
\Phi =& \Phi_1 + \Phi_2\\
=& \dfrac{\pi}{2} + 0\\
=& \dfrac{\pi}{2}
\end{align*}
\]
Exemplo 06
Calcule o fluxo de $\mathbf{F} = x \,\mathbf{j} $ através da superfície $S$ definida por $y=1+x^2+z^2$ para $1 \leq y \leq 5$ com $S$ orientada apontando na direção negativa de $y$.
SOL.
Obviamente esta superfície é uma superfície definida de forma explicita,
por tanto o vetor normal está dado pela seguinte equação
\[
\mathbf{n}_{1}=-\dfrac{\partial F}{\partial x}\,\mathbf{i}+\mathbf{j}-\dfrac{\partial F}{\partial z}\,\mathbf{k}
\nonumber
\]
onde
\[
y=F(x,z)=1+x^{2}+z^{2}
\nonumber
\]
de forma que
\[
\mathbf{n}_{1}=-2x\,\mathbf{i}+\mathbf{j}+2z\,\mathbf{k}
\nonumber
\]
Observe que este vetor é o vetor que aponta na direção positiva de
$\mathbf{j}$, de forma que o vetor norma que devemos utilizar é
\[
\begin{align*}
\mathbf{n}= & -\mathbf{n}_{1}\\
= & 2x\,\mathbf{i}-\mathbf{j}+2z\,\mathbf{k}
\end{align*}
\]
Como o campo já está escrito em termos da variável adequada passamos
a calcular o produto escalar
\[
\mathbf{F}\cdot\mathbf{n}=-x^{2}
\nonumber
\]
A região de integração está dada por
\[
\begin{array}{ccccc}
1 & \leq & y & \leq & 5\\
1 & \leq & 1+x^{2}+z^{2} & \leq & 5\\
0 & \leq & x^{2}+z^{2} & \leq & 4
\end{array}
\nonumber
\]
de forma que
\[
\Phi=\iint_{0\leq x^{2}+z^{2}\leq4}x^{2}\, dx\, dy
\nonumber
\]
escrevendo em coordenadas polares
\[
\begin{align*}
\Phi= & -\int_{0}^{2\pi}\int_{0}^{2}r^{2}\,\cos^{2}\theta\, r\, dr\, d\theta\\
= & -\int_{0}^{2\pi}\int_{0}^{2}r^{3}\cos^{2}\theta\, dr\, d\theta\\
= & -\dfrac{2^{4}}{4}\int_{0}^{2\pi}\cos^{2}\theta\, d\theta\\
= & -4\int_{0}^{2\pi}\cos^{2}\theta\, d\theta
\end{align*}
\]
utilizando
\[
2\cos^{2}\theta=1+\cos2\theta
\nonumber
\]
temos
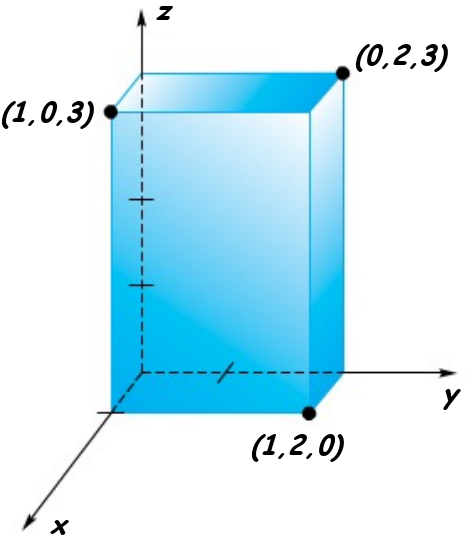
Exemplo 07
Calcule o fluxo do campo
\[
\mathbf{F}(x,y,z) = x^2y\,\mathbf{i} + 2xz \,\mathbf{j} + yz^3 \,\mathbf{k}
\nonumber
\]
através da superfície mostrada na figura ao lado.
SOL.
Para calcular a o fluxo do campo sobre a superfície devemos calcular o fluxo do campo sobre cada uma das seis faces do paralelepípedo e no fim somar o resultado de cada fluxo.
Assim, para a face $x=1$ temos que $\mathbf{n}=\mathbf{i}$ por tanto
\[
\begin{align*}
\mathbf{F}\cdot \mathbf{n}=&\left( x^2y\,\mathbf{i} + 2xz \,\mathbf{j} + yz^3 \,\mathbf{k} \right) \cdot \mathbf{i}\\
&x^2y\\
=& \left( 1 \right)^2y\\
=& y
\end{align*}
\]
dessa forma
\[
\begin{align*}
\Phi =& \iint_S \mathbf{F}\cdot \mathbf{n}\\
=&\int_0^3\int_0^2 y\,dy\,dz\\
=& 6
\end{align*}
\]
Cálculos similares nos levam a construir a seguinte tabela
| Face | $\displaystyle \mathbf{n}$ | $\displaystyle \mathbf{F}\cdot \mathbf{n}$ | $\displaystyle \iint_S \mathbf{F}\cdot \mathbf{n}$ |
|---|---|---|---|
| $x=1$ | $\displaystyle \mathbf{i}$ | $\displaystyle y$ | $\displaystyle 6$ |
| $x=0$ | $\displaystyle -\mathbf{i}$ | $\displaystyle 0$ | $\displaystyle 0$ |
| $y=2$ | $\displaystyle \mathbf{j}$ | $\displaystyle 2xz$ | $\displaystyle 9/2$ |
| $y=0$ | $\displaystyle -\mathbf{j}$ | $\displaystyle -2xz$ | $\displaystyle -9/2$ |
| $z=3$ | $\displaystyle \mathbf{k}$ | $\displaystyle 27y$ | $\displaystyle 54$ |
| $z=0$ | $\displaystyle -\mathbf{k}$ | $\displaystyle 0$ | $\displaystyle 0$ |
Exemplo 08
A equação
\[
z = 12,\;\;\;\;\;\;x^2+y^2\leq 25
\nonumber
\]
descreve um disco de raio $5$ que está no plano $z=12$. Suponha que o campo vetorial está dado por
\[
\mathbf{F}(x,y,z) = x\,\mathbf{i} + y \,\mathbf{j} + z \,\mathbf{k}
\nonumber
\]
calcule o fluxo do campo através da superfície.
SOL.
Neste problema devemos prestar atenção ao fato de que a superfície está definida pela equação $\displaystyle z=12$ (restringida a um círculo) e não pela equação $x^2+y^2=25$ a qual define um tubo.
Temos uma superfície definida de forma implícita, por tanto o vetor normal está dado por
\[
\begin{align*}
f= & z-12\\
\vec{\nabla f}= & \mathbf{k}\\
\vec{\nabla f}\cdot\mathbf{k}= & 1
\end{align*}
\]
de forma que
\[
d\vec{\sigma} = \mathbf{k}\,dx\,dy
\nonumber
\]
assim
\[
\begin{align*}
\Phi =& \iint_S \mathbf{F}\cdot d\vec{\sigma}\\
=& \iint_{x^2+y^2\leq 25} \left( x\,\mathbf{i} + y \,\mathbf{j} + z \,\mathbf{k} \right) \cdot\mathbf{k} \,dx\,dy\\
=&\iint_{x^2+y^2\leq 25} z\,dx\,dy
\end{align*}
\]
utilizando o fato de que $z = 12$ e escrevendo em coordenadas polares
\[
\begin{align*}
\Phi =& 12\int_0^5\int_0^2\pi r\,d\theta\,dr\\
=& 24\pi\int_0^5 r\,dr\\
=& \left( 24\pi \right)\left( \dfrac{25}{2} \right)\\
=&300\pi
\end{align*}
\]
Exemplo 09
Encontre o fluxo de $\mathbf{F}=yz\,\mathbf{i}+x\,\mathbf{j}-z^{2}\,\mathbf{k}$ através do cilindro parabólico $y=x^{2}$, $0\leq x\leq1$, $0\leq z\leq4$, na direção indicada na figura
SOL.
Neste caso a superfície $f=x^{2}$ está definida de forma explicita e é projetada no plano $xz$ com a normal tendo componente apontando na direção de $-\mathbf{j}$, por tanto
\[
\begin{align*}
\mathbf{n}= & \dfrac{\partial f}{\partial x}\,\mathbf{i}-\mathbf{j}+\dfrac{\partial f}{\partial z}\,\mathbf{k}\\
= & 2x\,\mathbf{i}-\mathbf{j}\\
d\vec{\sigma}= & \left(2x\,\mathbf{i}-\mathbf{j}\right)dx\, dz
\end{align*}
\]
escrevendo o campo em termos de $x,\, z$
\[
\begin{align*}
\mathbf{F}= & yz\,\mathbf{i}+x\,\mathbf{j}-z^{2}\mathbf{k}\\
= & x^{2}z\,\mathbf{i}+x\,\mathbf{j}-z^{2}\mathbf{k}
\end{align*}
\]
dessa forma
\[
\begin{align*}
\Phi= & \iint_{\begin{array}{c}
0\leq x\leq1\\
0\leq z\leq4
\end{array}}\left(x^{2}z\,\mathbf{i}+x\,\mathbf{j}-z^{2}\mathbf{k}\right)\left(2x\,\mathbf{i}-\mathbf{j}\right)dx\, dz\\
= & \int_{0}^{4}\int_{0}^{1}\left(2x^{3}z-x\right)dx\, dz\\
= & \dfrac{1}{2}\int_{0}^{4}\left(z-1\right)dz\\
= & 2
\end{align*}
\]