Teorema de Stoke
O teorema de Stokes junto com o teorema da Divergê'ncia ou de Gauss são os dos teoremas centrais do cálculo vetorial. Eles estendem o teorema de Green-Ostrogradsk, que é a versão bidimensional de ditos teoremas.
Ainda que o teorema receba o nome de George Stoke, não foi ele que descobriu esse teorema e ao parecer foi o Lord Kelvin, contudo foi Stokes quem o popularizou ao aplicar em uma serie de testes realizados em Cambridge.
Teorema de Green
A fim de introduzirmos o teorema de Stoke primeiro vejamos o caso particular que se aplica para o caso de superfícies definidas em um sistema bidimensional.
O teorema de Green nos permite calcular a integral de linha de um campo vetorial de uma outra forma. Para ver isso consideremos um campo vetorial $\mathbf{F}(x,y)$ tal que \[ \mathbf{F}(t) = P(x,y)\,\mathbf{i} + Q(x,y)\,\mathbf{j}\\ nonumber \]
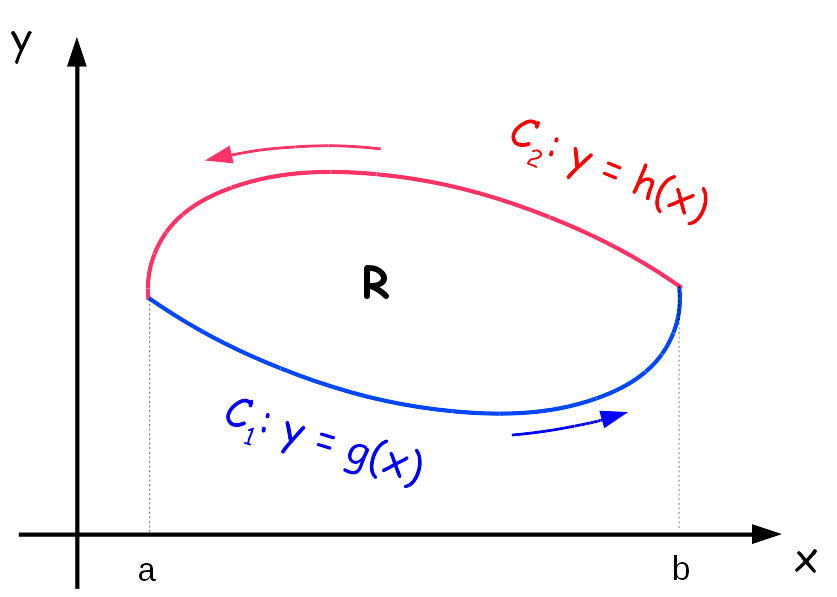
Consideremos duas curvas as quais se interceptam nos pontos $x=a$ e $x=b$, tal e como mostra o desenho acima. Agora vamos calcular a circulação ao longo desse caminho (integral de linha no circuíto fechado). \[ \begin{align*} \oint_C \mathbf{F}\cdot d\mathbf{s}=& \end{align*} \]