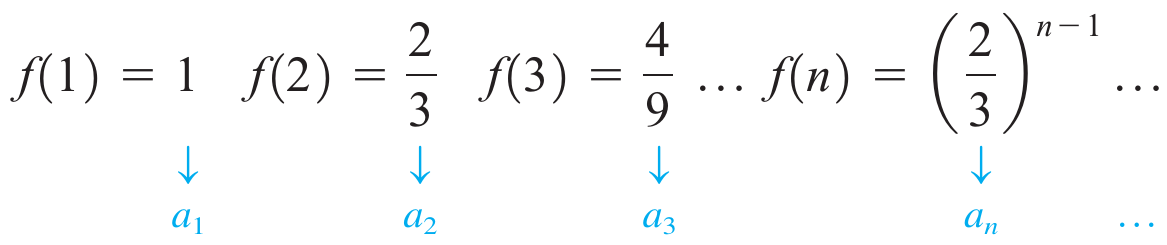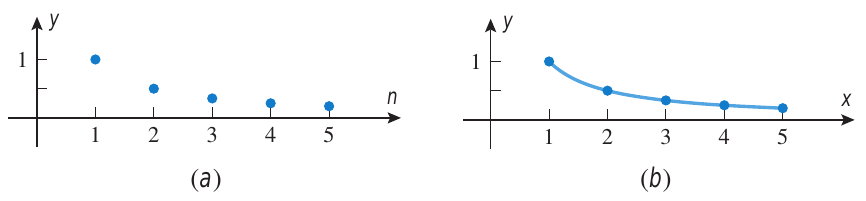Sequências

A ideia corriqueira que temos sobre o termo sequência descreve de forma bastante corretamente o que significa do ponto de vista matemática. Quando narramos algum episodio fortuito do nosso dia expomos de forma cronológica cada um dos eventos que compõem aquele episodio, igualmente utilizamos o conceito de sequência quando analisamos o resultado do brasileirão, colocamos as equipes em alguma ordem, ou descendente ou ascendente. De forma que vemos que intrinsecamente a palavra sequência implica em um conjunto de coisas que mantêm algum relação de ordem, de fato o conjunto dos números naturais apresenta esta característica, é um conjunto onde os elementos são colocados de forma que somando um ao anterior obtemos o número atual. Neste último exemplo resulta evidente que existem sequências nas quais é possível estabelecer uma relação "funcional" entre seu elementos, com esto em mente damos uma definição formal ao conceito matemático de sequência:

Definição

Uma sequência de números reais é uma função de $\mathrm {n}=\{1,2,3,\ldots\}$ em $\mathbb{R}$ a qual associa a cada número natural $n$ (inteiros positivos) o número real $a_n$ ($a$ índice $n$): \[ \begin{array}{clcr} s: & \mathbb{N} & \rightarrow & \mathbb{R}\\ & s(n) & = & a_n \end{array} \nonumber \]

Representaremos por $\left( a_n \right)$ a sequência cujo termo geral é $x_n$ (outra notação utilizada é $\{x_n\}$ e $\{x_n\}_{n=inicio}^{fim}$, mas essa mesma notação é utilizada por alguns para indicar o conjunto de elementos da sequência). Progressões aritméticas e geométricas são exemplo de sequências quando estas tiverem uma infinidade de termos.

Exemplo 01

Expresse a seguintes sequências determinando o termo geral

1. $\displaystyle 4,\;8,\;12,\;16,\;\ldots$
2. $\displaystyle 4,\;7,\;10,\;13,\;\ldots$
3. $\displaystyle 1,\;-1,\;1,\;-1,\;1,\;-1,\;\ldots$
4. $\displaystyle 7,\;7,\;7,\;7,\;\ldots$
5. $\displaystyle -\dfrac {1} {5},\;-\dfrac {4} {9},\;-\dfrac {7} {13},\;-\dfrac {10} {17},\;\ldots$
6. $\displaystyle 3+\dfrac {1} {2},\;3-\dfrac {1} {4},\;3+\dfrac {1} {8},\;3-\dfrac {1} {16},\;\ldots$
7. $\displaystyle 1,\;8-\dfrac {1} {4},\;\dfrac {1} {3},\;8-\dfrac {1} {8},\;\dfrac {1} {5},\;8-\dfrac {1} {12},\;\ldots$

Em muitas sequências não é possível determinar uma expressão que caraterize o termo geral, por exemplo na sequência cujo $n-\text{ésimo}$ termo é o $n-\text{ésimo}$ algarismo da representação decimal: $ \pi =3,1,4,1,5,9,2,\ldots$, outro exemplo é a sequência de números primos $2,3,5,7,11,\ldots$

Gráficos

Podemos representar os pontos da sequência em gráficos, mas nesses gráficos cada par ordenado não pode ser ligado aos outros pares vizinho por uma linha já que eles não formam um continuo. A representação gráfica pode ser útil para visualizar o comportamento do $n-\text{ésimo}$ termo $a_n$ quando $n$ cresce indefinidamente.

sequências definidas recursivamente

Algumas sequências não resultam de uma formula para o termo geral, no lugar disso é dada uma formula ou conjunto de formulas que especificam como gerar cada termo da sequência a partir dos termos que o precedem; dizemos que tais sequências são definidas recursivamente, e chamamos as formulas que as definem de formulas de recursão. Um exemplo deste tipo de sequência é a formula utilizada para aproximar a raiz quadrada de um número $a$: \[ x_1=1,\;\;\;\;\;\;\;\;\;\;x_{n+1}=\dfrac {1} {2}\left( x_{n}+\dfrac {a} {x_{n}}\right) \nonumber \]

Um outro exemplo famoso é a sequência de Fibonacci, definida como \[ f_1 = 1,\;\;\;\;f_2 = 1, \;\;\;\;f_n = f_{n+1} + f_{n-2}, \;\;\;\; n\geq 3 \nonumber \]

Limite de uma sequência

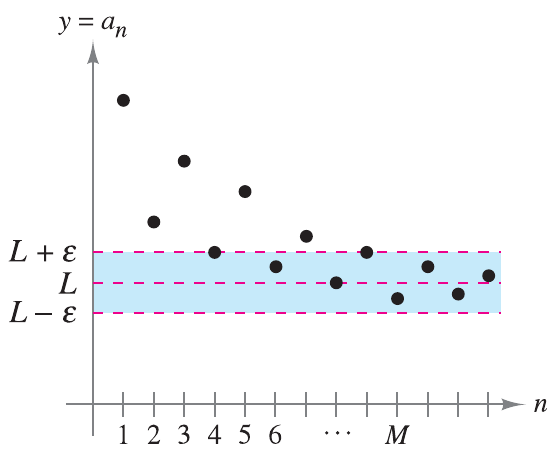
Através do cálculo do limite de uma sequência pretendemos obter informação sobre o comportamento de $a_n$ quando $n\to \infty$. Assim, diremos que uma sequência $\left( x_n \right)$ tende a um limite $L$ se os termos da sequência tornarem-se arbitrariamente próximos de $L$.

Definição

A sequência $\left( a_n \right)$ tem o limite $L$ se para qualquer $\epsilon > 0$ existir um número $M > 0$, tal que se $n$ for um inteiro e \[ \text{se } n > M, \text{ então } \left| a_n - L \right| < \epsilon \nonumber \] e escrevemos \[ \lim_{n \to +\infty} a_n = L \nonumber \] ou, simbolicamente \[ \lim_{n\to+\infty}a_{n}=L\Leftrightarrow\forall\epsilon>0,\,\exists M\in\mathbb{N}: n>M\Rightarrow\left|a_{n}-L\right|<\epsilon \nonumber \]

Exemplo

Utilize a definição anterior para provar que a sequência \[ \left(\dfrac{n}{2n+1}\right) \nonumber \] tem limite $1/2$

Teorema

Seja $L$ um número real. Seja $f$ uma função de uma variável real tal que \[ \lim_{x \to +\infty} f(x)= L \nonumber \] Se $\left( a_n \right)$ é uma sequência tal que $f(n)=a_n$ para todo número positivo $n$, então \[ \lim_{x \to +\infty} a_n = L \nonumber \]

Aqui devemos realizar uma observação. Se $L$ é o limite da sequência, implicitamente admitimos que o limite é único. Esta observação é expressada como um teorema conhecido como teorema da unicidade.

Exemplo

Encontre o limite da sequência se o $n-$ésimo termo está dado por \[ a_{n}=\left( 1+\dfrac {1} {n}\right) ^{n} \nonumber \]

Definição

Se uma sequência $\left( a_n \right)$ tiver um limite, dizemos que ela é convergente, e $\left( a_n \right)$ converge para o limite. Se a sequência não for convergente, ela será divergente.

Exemplo

Determine se a sequência

1. $\displaystyle \left( \dfrac {4n^{2}} {2n^{2}+1} \right)$
2. $\displaystyle \left( r^n \right)$, $\left|r \right| < 1$
3. $\displaystyle \left( ( -1)^{n}+1 \right)$
4. $\displaystyle \left( n\sin \dfrac {\pi } {n} \right)$

é convergente ou divergente.

Teorema

Se $\left( a_n \right)$ e $\left( b_n \right)$ forem sequência convergentes e $c$ for uma constante, então a sequência constante $\left( c \right)$ tem $c$ como seu limite; $\displaystyle \lim_{n \to +\infty} \left( c\,a_n\right) = c\,\lim_{n \to +\infty} a_n$; $\displaystyle \lim_{n \to +\infty} \left( a_n \pm b_n\right) = \lim_{n \to +\infty} a_n \pm \lim_{n \to +\infty} b_n$; $\displaystyle \lim_{n \to +\infty} a_n\, b_n= \left(\lim_{n \to +\infty} a_n\right)\left(\lim_{n \to +\infty} b_n\right)$; $\displaystyle \lim_{n \to +\infty} \dfrac{a_n}{b_n} = \dfrac{\displaystyle \lim_{n \to +\infty} a_n}{\displaystyle \lim_{n \to +\infty} b_n}$ se $\displaystyle \lim_{n \to +\infty} b_n \neq 0$ e todo $b_n \neq 0$

Exemplo

Determine se as sequências

1. $\displaystyle \left( \dfrac {n^{2}} {2n+1}\sin \dfrac {\pi } {n}\right)$
2. $\displaystyle \left( 3 + (-1)^n \right)$
3. $\displaystyle \left( \dfrac{n}{1-2n} \right)$
4. $\displaystyle \left( \dfrac{2n^2-n-1}{5n^2+n-3} \right)$
$\displaystyle \left( \sqrt{n^2+2n} -n \right)$

são, ou não, convergente e calcule seu limite.

Exemplo

Mostre que as sequências, as quais tem por $n$-ésimo termo

1. $\displaystyle a_n = \dfrac{n^2}{2^n-1}$
2. $\displaystyle a_n = n\arctan \dfrac{1}{n}$
3. $\displaystyle a_n = \dfrac{n}{e^n}$
4. $\displaystyle a_n = \left(\dfrac{n+1}{n-1}\right)^n$

convergem

Teorema do Sanduíche

Se \[ \lim_{x\to \infty} a_n = L = \lim_{x\to \infty} b_n \nonumber \] e existe um inteiro $M$ tal que $\displaystyle a_n \leq c_n \leq b_n$, $\forall \; n > M$, então \[ \lim_{x\to \infty} c_n = L \nonumber \]

Exemplo

Mostre que as sequências

1. $\displaystyle \left( (-1)^n\dfrac{1}{n!} \right)$
2. $\displaystyle \left( \dfrac{\cos n}{n} \right)$

convergem e determine seus limites.

Definição de função vetorial

Se \[ \lim_{x\to \infty} \left| a_n \right| = 0 \nonumber \] então \[ \lim_{x\to \infty} a_n = 0 \nonumber \]

Limites frequentes

1. $\displaystyle \lim_{x \to \infty}\, \dfrac{\ln n}{n}=0$
2. $\displaystyle \lim_{x \to \infty}\, a^{1/n}=1,\;\;\;(a > 0)$
3. $\displaystyle \lim_{x \to \infty}\, \left(1+\dfrac{a}{n}\right)^n=e^x$
4. $\displaystyle \lim_{x \to \infty}\, \sqrt[n]{a}=1$
5. $\displaystyle \lim_{x \to \infty}\, a^n=0,\;\;\;(|a| < 1)$
6. $\displaystyle \lim_{x \to \infty}\, \dfrac{a^n}{n!}=0,\;\;\;(\forall a)$

Exemplo

Determine o limite

1. $\displaystyle \lim_{x \to \infty}\, \dfrac {\ln \left( n^{2}\right) } {n}$
2. $\displaystyle \lim_{x \to \infty}\, \left( \dfrac {n-2} {n}\right) ^{n}$

sequências monótonas e limitadas

Sequências aparecem em diversas situações física e portanto resulta importante determinar se a mesma converge ou não e isto é possível de se fazer mesmo não sendo possível determinar algum limite como os mencionados anteriormente, assim veremos agora alguns testes que nos permitiram determinar ou não a convergência.

Definição

Dizemos que uma sequência $\left( a_n \right)$ é crescente, se $a_n \leq a_{n+1},\;\forall\, n decrescente, se $a_n \geq a_{n+1},\;\forall\, n$ Chamaremos de monótona a uma sequência que seja crescente ou decrescente.

No caso de $a_n < a_{n+1}$, a sequência é estritamente crescente; se $a_n > a_{n+1}$, a sequência é estritamente decrescente. (Alguns autores chamam de não decrescente ao caso onde $a_n \leq a_{n+1}$ e de não crescente ao caso $a_n \geq a_{n+1}$)

Definição

Uma sequência $\left( a_n \right)$ tem uma \textbf{cota superior} se existir um número $M$ tal que \[ a_n \leq M\;\;\;\;\;\;\;\;\; \forall\,n \geq 1 \nonumber \] Ela tem uma \textbf{cota inferior} se existir um número $m$ tal que \[ a_n \geq m\;\;\;\;\;\;\;\;\; \forall\,n \geq 1 \nonumber \] Se ela tiver uma cota superior e inferior então $\left( a_n \right)$ é uma sequência limitada

O teorema a seguir aponta uma condição necessária e suficiente para a convergência da sequência.

Teorema

Uma sequência monótona limitada é convergente

Teorema

Seja $\left( a_n \right)$ uma sequência não decrescente, e suponhamos que $M$ seja a cota superior da sequência. Então, $\left( a_n \right)$ será convergente e \[ \lim_{x \to \infty} a_n \leq M \nonumber \]

Teorema

Seja $\left( a_n \right)$ uma sequência não crescente, e suponhamos que $m$ seja a cota inferior da sequência. Então, $\left( a_n \right)$ será convergente e \[ \lim_{x \to \infty} a_n \geq M \nonumber \]

Exemplo

Seja $a_n$ definido recursivamente por \[ a_1 = 1,\;\;\;\;\;\;\;\;a_{n+1}=\sqrt{6+a_n}\;\;\;\;\;\;\;\;(n=1,2,3,\ldots) \nonumber \] mostre que $\displaystyle \lim_{n \to \infty} a_n$ existe e encontre seu valor.

Exemplos