Testes de convergência para séries com termos positivos

Teste da divergência

Até aqui vimos 3 exemplos de series, 2 deles convergentes e um divergente. A continuação vamos apresentar um teorema onde se estabelece uma condição para sabermos se uma série diverge

Teorema: Teste da divergência

Se $\displaystyle \lim_{n\to \infty} a_n$ não existe ou $\displaystyle \lim_{n\to \infty} a_n \neq 0$, então a série $\displaystyle \sum_{n=1}^{\infty} a_n$ diverge.

Observe que este teorema afirma que a série diverge se $\displaystyle \lim_{n\to \infty} a_n \neq 0$, mas isso não significa que se $\displaystyle \lim_{n\to \infty} a_n = 0$ então a série vai convergir, ela pode ou não convergir, contudo sempre é verdade que toda serie convergente verifica o exposto no seguinte teorema

Teorema

Se $\displaystyle \sum_{n=1}^{\infty} a_n$ é convergente então $\displaystyle \lim_{n\to \infty} a_n = 0$.

Exemplo

Utilizando os teoremas anteriores analise a divergência ou não das seguintes séries

1. $\displaystyle \sum_{n=1}^{\infty} n^2$
2. $\displaystyle \sum_{n=1}^{\infty} \dfrac {n+1}{n}$
3. $\displaystyle \sum_{n=1}^{\infty} \left( -1\right)^{n+1}$
4. $\displaystyle \sum_{n=1}^{\infty} \dfrac {-n}{2n+5} $
5. $\displaystyle 1+\underbrace{\dfrac{1}{2}+\dfrac{1}{2}}\underbrace{\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}+}\cdots+\underbrace{\dfrac{1}{2^n}+\dfrac{1}{2^n}+\cdots+\dfrac{1}{2^n}+}\cdots$
6. $\displaystyle \sum_{n=1}^{\infty} \dfrac {n^2}{5n^2+4} $

Visualizando Séries

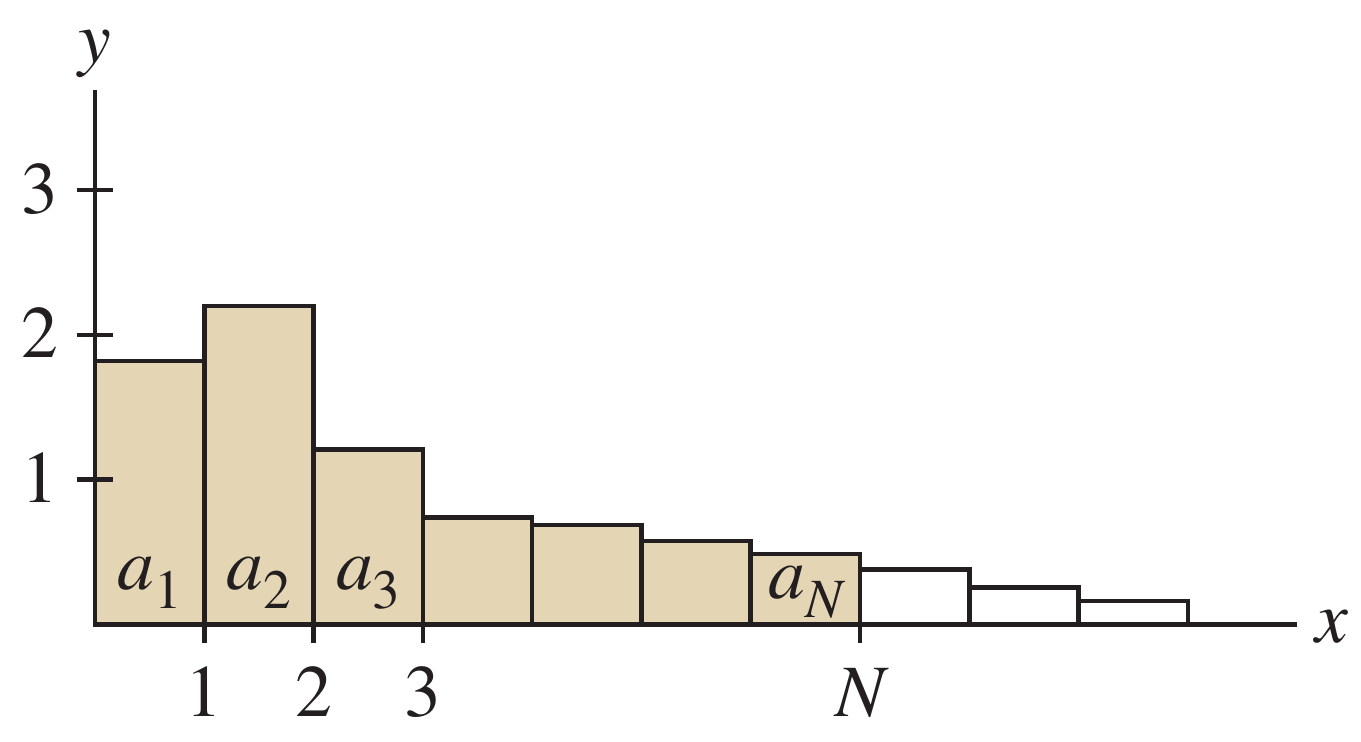
Antes de explicarmos o que é uma série com termos positivos resulta interessante introduzir um método de gráfico que nos permitira analisar o comportamento das séries. O método consiste em construir um gráfico de barras onde a largura de cada uma das barra é $1$ e a altura é o valor do coeficiente $a_n$, esse método pode ser visualizado na figura a seguir

Agora estamos em condição de definir o que é uma série de termos positivos, uma série com termos positivo são aquelas séries, $\displaystyle \sum a_n$, tais que $a_n > 0$, para todos os valores de $n$. Graficamente significa que todo o diagrama de barras está por cima do eixo, isto é

A partir de uma análise rápida de series de termos positivos podemos afirmar o seguinte teorema

Teorema: Dicotomia para séries positivas

Se $\displaystyle S = \sum a_n$ é uma série positiva, então ou A soma $S_N$ é limitada superiormente, nesse caso $S$ converge. Ou A soma $S_N$ não é limitada superiormente e nesse caso $S$ diverge.

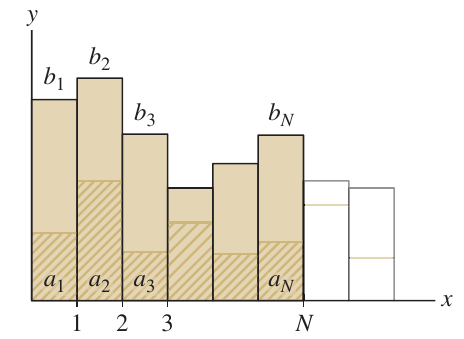
Critério de comparação

Suponha que $\sum_{n=1}^{\infty} a_n$ é $\sum_{n=1}^{\infty} b_n$ são séries de termos não negativos. Suponhamos que existe um $n_0 \in \mathbb{N}^*$ tal que $a_n \leq b_n$, para todo $n > n_0$. Então

1. Se $\displaystyle \sum_{n=1}^{\infty} b_n$ converge, então $\displaystyle \sum_{n=1}^{\infty} a_n$ também converge.
2. Se $\displaystyle \sum_{n=1}^{\infty} b_n$ diverge, então $\displaystyle \sum_{n=1}^{\infty} a_n$ também diverge.

A figura acima mostra claramente este critério, obviamente que se a área de $\displaystyle \sum_{n=1}^{\infty} b_n$ é finita, $\displaystyle \sum_{n=1}^{\infty} a_n$ também é.

Exemplos

1. $\displaystyle \sum_{n=1}^{\infty} \dfrac {1} {\sqrt {n}} $
2. $\displaystyle \sum_{n=1}^{\infty} \dfrac {1} {\sqrt[3]{n}}$
3. $\displaystyle \sum_{n=1}^{\infty} \dfrac {5} {3+7^{n}}$
4. $\displaystyle \sum_{n=1}^{\infty} \dfrac {1} {n^{n}} $ (série-p)
5. $\displaystyle \sum_{n=1}^{\infty} \dfrac {1} {\ln n}$
6. $\displaystyle \sum_{n=1}^{\infty} \dfrac {1} {5n+19}$
7. $\displaystyle \sum_{n=1}^{\infty} \dfrac {1} {\sqrt {n^{2}+4n}}$

Critério de comparação com limite

Suponha $\displaystyle \sum_{n=1}^{\infty} a_n$ e $\displaystyle \sum_{n=1}^{\infty} b_n$ duas séries de termos positivos. Seja $c$ definido por \[ c = \displaystyle \lim_{n\to \infty}\dfrac{a_n}{b_n} \]

1. Se $c > 0$, então ambas das séries convergem, ou ambas divergem.
2. Se $c = 0$, e se $\displaystyle \sum_{n=1}^{\infty} b_n$ converge, então $\displaystyle \sum_{n=1}^{\infty} a_n$ converge.
3. Se $c = \infty$ e se $\displaystyle \sum_{n=1}^{\infty} b_n$ diverge, então $\displaystyle \sum_{n=1}^{\infty} a_n$ diverge.

Exemplos

Utilize o teste da comparação com limite para determinar se as seguintes séries convergem ou divergem

1. $\displaystyle \sum_{n=1}^{\infty} \dfrac {n^{2}+5} {n^{3}+n+2}$
2. $\displaystyle \sum_{n=1}^{\infty} \dfrac {1} {1+\sqrt {n}}$
3. $\displaystyle \sum_{n=1}^{\infty} \dfrac {1+\sin n} {n^{2}}$

Critério da integral

Uma série converge se a área total dos retângulos na representação gráfica for finita e a soma da série for a área total dos retângulos, de forma que podemos estabelecer o seguinte teorema (observe que por $f$ ser positiva, implica que os termos da série são positivos)

Teste da integral

Se $f$ é positiva, continua e decrescente para $x\geq 1$ e $a_n = f(n)$, então \[ \displaystyle \sum _{n=1}^{\infty } a_n\;\;\;\;\;\text{ e } \;\;\;\;\; \int_1^\infty f(x) dx \] ambas convergem ou ambas divergem.

Exemplos

1. $\displaystyle \sum _{n=1}^{\infty } \dfrac {1} {n^{n}} $
2. $\displaystyle \sum _{n=1}^{\infty } ne^n $
3. $\displaystyle \sum _{n=1}^{\infty } \dfrac {1} {n\ln n} $

O I exemplo desta série no leva a propor o seguinte teorema

Séries $p$

A p-serie \[ \displaystyle \sum _{n=1}^{\infty } \dfrac{1}{n^p}=\dfrac{1}{1^p}+\dfrac{1}{2^p}+\dfrac{1}{3^p}+\ldots \] converge se $p > 1$ diverge se $0< p \leq 1$

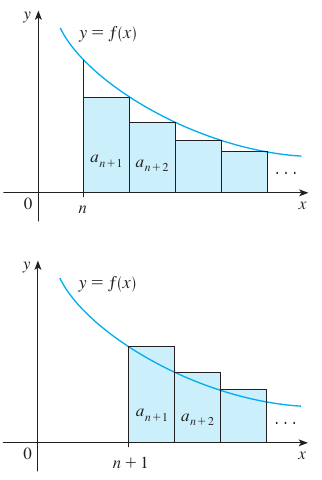
Quando iniciamos o estudo de series nos perguntamos como era possível somar um conjunto infinito de coisas, a resposta parcial a este fato pode ser encontrado através do uso das séries parciais. Contudo, nem sempre essa técnica pode ser aplicada de forma simples é por isso que estudamos alguns critério que permitam rapidamente determinar se uma série é ou não convergente. Mas suponha que em lugar de calcular somar toda a série só somamos uns poucos termos da série (uma soma parcial), agora basta saber quão afastados estamos do resultado final, ou seja, quanto vale o resto

A partir da integral da função podemos delimitar o valore desse resto. Observe a figura anterior, note que o resto (soma dos $a_n$) é o superestimada ou subestimada pela integral, de forma que podemos escrever que o resto de ordem $R_n$ fica delimitado por \begin{array}{lcccr} \displaystyle \int _{n+1}^{\infty }f\left( x\right) dx &\leq & R_n & \leq & \displaystyle \int _{n}^{\infty }f\left( x\right) dx \end{array} como \[ S = s_n + R_n \] onde $s_n$ é a soma parcial que tínhamos avaliado e $S$ é a soma da série, então \begin{array}{lcccr} s_n +\displaystyle \int _{n+1}^{\infty }f\left( x\right) dx &\leq & s_n + R_n & \leq & sn + \displaystyle\int _{n}^{\infty }f\left( x\right) dx\\ &&&\\ s_n +\displaystyle \int _{n+1}^{\infty }f\left( x\right) dx &\leq & S & \leq & s_n + \displaystyle \int _{n}^{\infty }f\left( x\right) dx\\ \end{array}

Exemplo

1. Estime a soma da série $\displaystyle \sum \dfrac{1}{n^2}$ usando o teorema anterior e $n=10$
2. Repita o procedimento para $\displaystyle \sum \dfrac{1}{n^3}$