Teste de convergência para séries com termos não todos positivos
Até este ponto todos os critérios que analisamos dependiam da série ser constituída por termos positivos, agora essa condição sera flexibilizada
| Teorema |
|
Seja $\displaystyle \sum_{n=1}^{\infty} a_n$ uma série qualquer. Se a série $\displaystyle \sum_{n=1}^{\infty} \left|\,a_n\,\right|$ converge, então $\displaystyle \sum_{n=1}^{\infty} a_n$ também converge. |
Critério da razão
Seja $\displaystyle \sum_{n=1}^{\infty} a_n$ uma série para a qual $a_n \neq 0$, e seja \[ L = \lim_{x\to \infty} \; \left| \dfrac {a_{n+1}} {a_{n}}\right| \] então:
- Se $L < 1$, a série $\displaystyle \sum_{n=1}^{\infty} a_n$ é convergente.
- Se $L > 1$, ou $L = \infty$, a série $\displaystyle \sum_{n=1}^{\infty} a_n$ é divergente.
- Se $L = 1$ o critério não pode ser utilizado.
Exemplo
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {n} {2^{n}}$
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {n!} {2^{n}}$
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {n!} {n^{n}}$
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {2\cdot 5\cdot 8\cdots \left( 3n+1\right) } {5\cdot 9\cdot 13\cdots \left( 4n+1\right) } $
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {\left( -2\right) ^{n}\,n!} {\left( 2\,n\right) !} $
- Para quais valores de $x$ a converge a série $\displaystyle \sum_{n=1}^{\infty} \dfrac {x^{2n-1}} {2n-1}$
Critério da raiz
eja $\sum a_n$ uma série numérica qualquer. Seja $L$ definido por \[ \lim _{n\rightarrow \infty }\sqrt [n] {\left| a_{n}\right| } \] Então
- Se $L<1$, a série converge.
- Se $L>1$ ou $L = \infty$, a série diverge.
- Se $L = 1$, o critério não pode ser utilizado.
Exemplo
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {1} {\left( \ln n\right) ^{n}} $
- $\displaystyle \sum_{n=1}^{\infty} n\,a^n \;$ $(a \in \mathbb{R})$
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {n1+n^{2}} {\left( n+1\right) ^{n2}} $
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {e^{na}\left( n+1\right) ^{3n}} {n^{3n-2}}\;$ $(a \in \mathbb{R})$
OBSERVAÇÃO:
O critério da raiz é "mais forte" do que o critério da razão, no seguinte sentido: Se existe $\displaystyle \lim _{n\rightarrow \infty } \; \left| \dfrac {a_{n+1}} {a_{n}}\right|$, então também existe o $\displaystyle \lim _{n\rightarrow \infty }\sqrt [n] {\left| a_{n}\right| }$ e tem o mesmo valor, mas podemos existir $\displaystyle \lim _{n\rightarrow \infty }\sqrt [n] {\left| a_{n}\right| }$, sem existir $\displaystyle \lim _{n\rightarrow \infty } \; \left| \dfrac {a_{n+1}} {a_{n}}\right|$
Convergência absoluta
Diz-se que $\sum a_n$ é uma série
- absolutamente convergente se ambas $\displaystyle \sum_{n=1}^{\infty} a_n$ e $\displaystyle \sum_{n=1}^{\infty} \left|\,a_n\, \right|$ convergem,
- condicionalmente convergente se $\displaystyle \sum_{n=1}^{\infty} a_n$ convergem mas $\displaystyle \sum_{n=1}^{\infty} \left|\,a_n\, \right|$ diverge.
OBSERVAÇÃO:
Um exemplo típico de série que é condicionalmente convergente é a série \[ \displaystyle \sum_{n=1}^{\infty} \dfrac {\left( -1\right) ^{n+1}} {n}=1-\dfrac {1} {2}+\dfrac {1} {3}-\ldots \] que é uma série-p. Dessa forma uma série pode ser classificada como absolutamente convergente, condicionalmente convergentes ou divergentes. Obviamente séries positivamente definidas, se convergente, devem ser absolutamente convergentes. Outro fato interessante é que as séries absolutamente convergentes convergem mas depressa que as condicionalmente convergentes, em geral.
Séries alternantes
Se $a_n>0$ para todos os número inteiros positivos $n$, então a série \[ \displaystyle\sum _{n=1}^{\infty }\left( -1\right)^{n+1} a_n=a_{1}-a_{2}+a_{3}-a_4+\ldots + \left( -1\right)^{n+1}a_n+\ldots \] e a série \[ \displaystyle\sum _{n=1}^{\infty }\left( -1\right)^{n} a_n=-a_{1}+a_{2}-a_{3}+a_4-\ldots + \left( -1\right)^{n}a_n+\ldots \] são chamadas de séries alternantes.
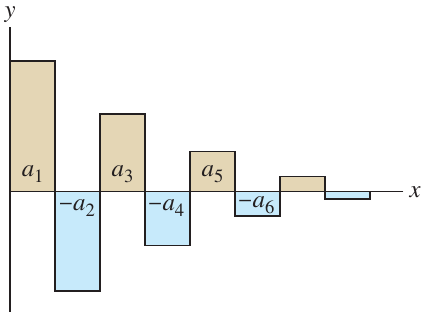
Figura 04: Uma série alternante com termos decrescentes, $\displaystyle a_n > a_{n+1}$. A soma é a área com sinal, a qual é dominada principalmente por $a_1$.
Critério de Leibniz ou critério das séries alternantes
A série alternante \[ \displaystyle\sum _{n=1}^{\infty }\left(-1\right)^{n}a_n \;\;\;\;\;\text{ ou }\;\;\;\;\; \displaystyle\sum _{n=1}^{\infty }\left(-1\right)^{n+1}a_n \] será convergente se as duas condições a seguir forem satisfeitas:
- $\displaystyle a_1 \geq a_2 \geq a_3 \geq \ldots \geq a_n \geq a_{n+1} \geq \ldots$
- $\displaystyle \lim_{n \to \infty} a_n =0$
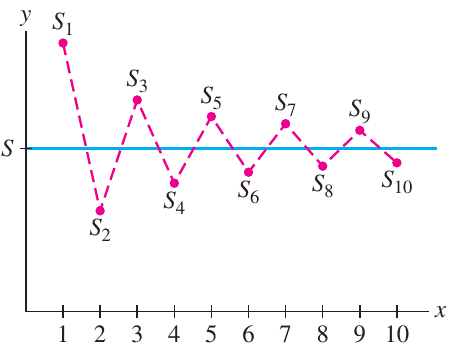
Figura 05: A somas parciais das séries alternantes oscila entorno do limite. As somas parciais impares decrescem e das somas parciais pares incrementa.
Exemplos
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {\left( -1\right) ^{n+1}} {n} $
- $\displaystyle \sum_{n=1}^{\infty} \dfrac {\left( -1\right) ^{n}} {\sqrt {n}} $
- $\displaystyle \sum_{n=1}^{\infty} \left( -1\right) ^{n}\dfrac {n} {5+2n} $
- $\displaystyle \sum_{n=1}^{\infty} \left( -1\right) ^{n}\dfrac {\ln n} {e^{n}} $
- $\displaystyle \sum_{n=1}^{\infty} \left( -1\right) ^{n+1}\dfrac {2n} {4n^{2}-3} $
