Funções vetoriais

No seu primeiro curso de cálculo foi introduzido e analisado conceito de função de uma variável real, $y=f(x)$ onde $x \in \mathbb{R}$. Sobre esse tipo de função foi definido o conceito de derivada e integral. No segundo curso de cálculo os conceito de derivada e integral são estendidos para funções de mais de uma variável, isto é $z=f(x_1,x_2,x_3,\ldots,x_n)$ onde os $\{x_1,x_2,x_3,\ldots,x_n\} \in \mathbb{R}^n$. Agora vamos continuar trabalhando com funções de muitas variáveis com a diferença de que utilizaremos o conceito de vetor (introduzido no curso de Física I) o qual terá por componentes funções mono ou multivariadas.

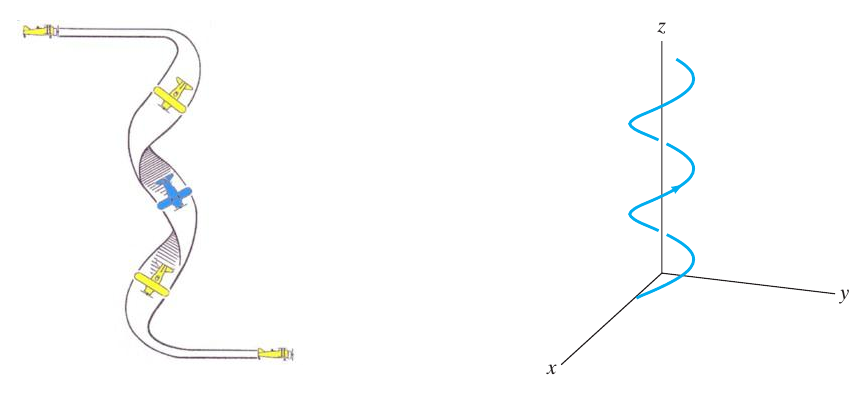
Para entender o conceito de função vetorial vamos considerar o seguinte exemplo. Suponha que um avião em um espetáculo aéreo executa uma movimento de queda livre seguindo uma trajetória em forma de parafuso. Será que é possível descrever a posição do avião em todo instante? Da Física sabemos que sim, mas matematicamente podemos dizer que a trajetória no espaço (isto é em $\mathbb{R}^3$) está descrita por uma função tal que $\mathbf{r}:\, \mathbb{R} \to \mathbb{R}^3$ já que teríamos um parâmetro $t \in \mathbb{R}$ (que fisicamente pode ser o tempo) e variação deste parâmetro nos permite calcular a posição do avião em cada coordenada espacial, $\{x,y,z\} \in \mathbb{R}^3$. Na verdade veremos em detalhe que a função que reproduz a trajetória é uma função dada pela expressão \[ \mathbf{r}(t) = \cos t\,\mathbf{i} + \sin t\,\mathbf{j} + t\,\mathbf{k} \nonumber \]

Mas não devemos supor que toda função vetorial é do tipo $\mathbf{r}:\, \mathbb{R} \to \mathbb{R}^3$, um exemplo claro disto é a função que descreve a velocidade da água (que é um vetor de três componente) , vertida desde um recipiente, obviamente a água terá velocidades diferentes em pontos diferente e pior ainda, a velocidade de em um mesmo ponto pode varia com o decorrer do tempo, por tanto a função que ha de descrever a velocidade deve ser da forma $\mathbf{v}:\, \mathbb{R}^4 \to \mathbb{R}^3$, isto é devemos saber $\{x,y,z,t\}$ para obter $\{v_x,v_y,v_z\}$. Um exemplo de uma função deste tipo é \[ \mathbf{v}(x,y,z,t) = xyzt\,\mathbf{i} + \left( x^2 - y^2 \right) \,\mathbf{j} + \left( 3z+t \right)\,\mathbf{k} \nonumber \]

Como dito no inicio, em ambos dos exemplos apresentados as funções vetoriais são vetores cujas componente são funções, funções escalares. Dizer que as componentes são funções escalares significa que, mesmo que esta função tenha varias variáveis, o resultado dela sempre será um número, matematicamente isto significa que se as variáveis que definem a função são n-uplas ordenadas $\mathbf{x} = (x_1, x_2, x_3, \ldots, x_n)$ as quais são escolhidas de um conjunto $A$ o qual é, por sua vez, um subconjunto de $\mathbb{R}^n$, ao aplicarmos a função obteremos um número que pertence aos Reais, ou seja $f(\mathbf{x}) \in \mathbb{R}$; escrevendo o anterior em notação matemática temos que se $f=f(\mathbf{x})=f(x_1, x_2, x_3, \ldots, x_n)$ é a função, então $f:A\subseteq \mathbb{R}^n \to \mathbb{R}$

Levando em consideração a forma funcional das componentes da função vetorial estas podem ser representadas de várias forma. A fim de exemplificar vamos supor que nossa função vetorial seja $\mathbf{f}:A\subseteq \, \mathbb{R}^n \to \mathbb{R}^3$ o que significa que cada função componente é multivariada mas a função resultante é um vetor num espaço $3D$, ou seja $\mathbf{f}(\mathbf{x}) \in \mathbb{R}^3 \, \wedge \,\mathbf{x} \in A$. A notação mais carateristica neste caso é expressar de forma vetorial a função tal como feito nos exemplos: \[ \mathbf{f}(\mathbf{x}) = f_1(\mathbf{x})\,\mathbf{i} + f_2(\mathbf{x}) \,\mathbf{j} + f_3(\mathbf{x}) \,\mathbf{k} \nonumber \] A outra notação utilizada é escrever a componente formando uma n-upla colocando ela entre parenteses \[ \mathbf{f}(\mathbf{x}) = \left( f_1(\mathbf{x}), \,f_2(\mathbf{x}), \, f_3(\mathbf{x}) \right) \nonumber \] ou como feito por outros autores: \[ \mathbf{f}(\mathbf{x}) = \left< f_1(\mathbf{x}), \,f_2(\mathbf{x}), \, f_3(\mathbf{x}) \right> \nonumber \] Nota: A esta altura você já deve ter identificado que os vetores são escrito em negrito (mesmo as funções vetoriais).

Funções vetoriais expressadas de forma paramétrica

Durante a maior parte deste curso estaremos tratando com funções vetoriais cujo conjunto imagem será $\mathbb{R}^n$, onde $n\leq 3$, as quais serão expressadas de forma paramétrica, isto é, são funções onde $\mathbf{f}:A\subseteq \, \mathbb{R} \to \mathbb{R}^n,\,n\leq 3$. Quando a função descreve uma curva unidimensional se acostuma utilizar como parâmetro a variável $t$, onde $t\in A \subseteq \mathbb{R}$. Se a função descreve uma superfície então utilizaremos se acostuma utilizar as variáveis $u$ e $v$.

Visualização de funções vetoriais

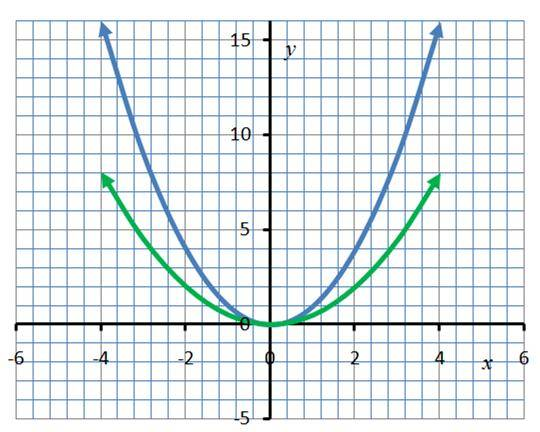
As vezes resulta prático e mais informativo ver a representação gráfica da função, quando a função é de um variável, $y = f(x)$, sabemos que a representação desta se da localizando no plano cartesiano os pontos formado pelo par ordenado formado pela abscisa e ordenada, $(x,y)$ o que resulta num gráfico em duas dimensões. Como exemplo temos a função quadrática, $f(x) = ax^2$, embaixo se mostra o gráfico da função

Mediante a utilização de funções vetoriais também podemos representar a mesma função de uma variável, por exemplono caso da função quadrática uma possível representação vetorial é $\mathbf{r}(x) = t \,\mathbf{i} + at^2 \,\mathbf{j}$ e o gráfico que obteremos é o mesmo. Contudo, utilizando funções vetoriais podemos explorar mais dimensões, como é no caso da função utilizada para modelar o parafuso realizado pelo avião.

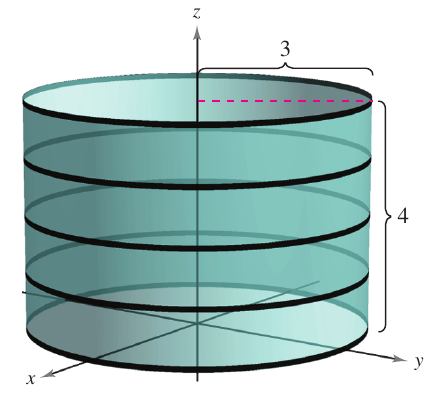
resulta obvio que nos exemplo acima colocados a estrutura que resulta (o gráfico) é uma estrutura unidimensional (a parábola e a hélice circular), mas também é possível obter estruturas de maior dimensionalidade utilizando funções vetoriais, como exemplo vejamos a função $\mathbf{r}(u,v) = 3\cos u\,\mathbf{i} + 3 \sin u \,\mathbf{j} + v \,\mathbf{k}$, onde $0 \leq u \leq 2\pi$ e $0 \leq v \leq 4$.

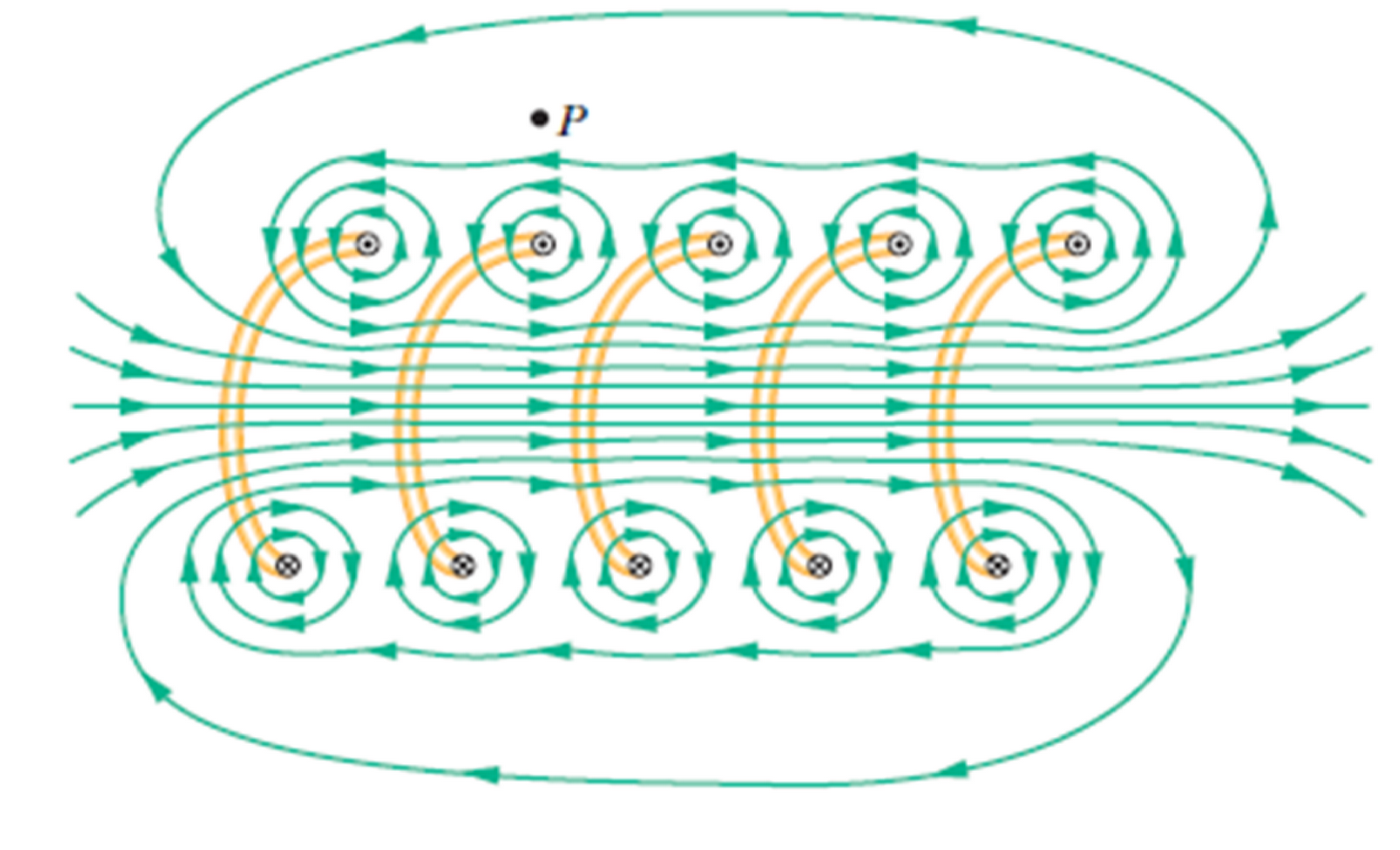
Uma outra representação gráfica das funções vetoriais é a utilizada para expressar a ideia de campo vetorial, na segunda área deste curso estudaremos em detalhe esse conceito, mas por enquanto basta saber que quando representamos um campo vetorial colocamos em cada ponto do espaço um vetorzinho que indica a direção, sentido e magnitude da grandeza representada, um exemplo é o campo magnético produzido por um bobina, como mostrado na figura

Operações com funções vetoriais

As funções vetoriais podem ser aplicadas as mesmas operações que o vetores convencionais possuem:

Operações com funções vetoriais

Considere as seguintes funções vetoriais \[ \mathbf{f}(t) = f_1\,\mathbf{i} + f_2 \,\mathbf{j} + f_3 \,\mathbf{k} \nonumber \] e \[ \mathbf{g}(t) = g_1\,\mathbf{i} + g_2 \,\mathbf{j} + g_3 \,\mathbf{k} \nonumber \] onde $t\in I \subseteq \mathbb{R}$, a partir destas funções podemos construir novas funções aplicando as seguentes operações entre elas: $\displaystyle \begin{align*} \mathbf{h}(t) &= \mathbf{f}(t) \pm \mathbf{g}(t)\\ &= \left( f_1 \pm g_1 \right) + \left( f_2 \pm g_2 \right) + \left( f_3 \pm g_3 \right) \end{align*} $ $\displaystyle \begin{align*} \mathbf{w}(t) &= \mathbf{f}(t) \times \mathbf{g}(t)\\ &=\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ f_1 & f_2 & f_3\\ g_1 & g_2 & g_3 \end{vmatrix}\\ &= \left(f_2\,g_3 - f_3\,g_2\right) \, \mathbf{i} - \left(f_3\,g_1 - f_1\,g_3\right) \, \mathbf{j} + \left(f_1\,g_2 - f_2\,g_1\right) \, \mathbf{k} \end{align*} $ $\displaystyle \begin{align*} \mathbf{h}(t) &= \mathbf{f}(t) \cdot \mathbf{g}(t)\\ &= f_1\, g_1 + f_2\,g_2 + f_2\,g_3 \end{align*} $

Limites e continuidade

A continuação vamos formular a definição formal de limite de uma função vetorial, notaremos que esta definição é uma extensão do conceito de limite estudado em cálculo I

Definição de limite

Seja $\mathbf{r}(t)$ uma função vetorial a qual está definida para todo $t$ em um intervalo aberto contendo o número $a$, excepto possivelmente no próprio $a$. Escrevemos \[ \lim_{t \to a}\, \mathbf{r}(t) = \mathbf{L} \nonumber \] se para qualquer $\epsilon > 0$ podemos encontrar um $\delta > 0$ (o qual deve, em geral, depender de $\epsilon$) tal que se $0 < \left| t - a\right| < \delta$, então $\left| \mathbf{r}(t) - \mathbf{L}\right| < \epsilon$

Isto significa que se escolhemos um valor de $t$ entre $a-\delta$ e $a+\delta$ o vetor diferença $\mathbf{r}(t) - \mathbf{L}$ estará dentro de uma esfera de radio $\epsilon$.

A forma mais geral das funções vetoriais de que trataremos nesta primeira área são aquelas definidas por \[ \mathbf{r}(t) = f(t)\,\mathbf{i} + g(t) \,\mathbf{j} + h(t)\,\mathbf{k} \nonumber \] Assim o limite $\displaystyle \lim_{t \to a}\, \mathbf{r}(t)$ existe se os limites \[ \lim_{t \to a}\, f(t);\;\;\;\;\;\lim_{t \to a}\, g(t);\;\;\;\;\;\lim_{t \to a}\,h(t) \nonumber \] existem, isto é \[ \lim_{t \to a}\, \mathbf{r}(t) = \lim_{t \to a}\, f(t)\,\mathbf{i}+ \lim_{t \to a}\, g(t)\,\mathbf{j}+ \lim_{t \to a}\,h(t)\,\mathbf{k} \nonumber \]

Propriedades dos limites de funções vetoriais

Sejam $\mathbf{f}(t)$ e $\mathbf{g}(t)$ duas funções vetoriais e $h(t)$ uma função real, definida no mesmo intervalo, se \[ \lim_{t \to t_0}\, \mathbf{f}(t) = \mathbf{a}\;\;\;\; \lim_{t \to t_0}\, \mathbf{g}(t) = \mathbf{b}\;\;\;\;\lim_{t \to t_0}\, h(t) = m \nonumber \] então $\displaystyle \lim_{t \to t_0}\, \left[ \mathbf{f}(t) \pm \mathbf{g}(t)\right] = \mathbf{a} + \mathbf{b}$ $\displaystyle \lim_{t \to t_0}\, \mathbf{f}(t) \cdot \mathbf{g}(t) = \mathbf{a} \cdot \mathbf{b}$ $\displaystyle \lim_{t \to t_0}\, \mathbf{f}(t) \times \mathbf{g}(t) = \mathbf{a} \times \mathbf{b}$ $\displaystyle \lim_{t \to t_0}\, h(t)\,\mathbf{f}(t) \cdot \mathbf{g}(t) = m\mathbf{a}$

A partir do conceito de limite podemos dar as condições necessárias que devem ser verificas por uma função vetorial para ser considerada continua

Definição de função vetorial continua

A função $\mathbf{r}(t)$ com valores vetoriais será contínua em $a$ se e somente se as três condições seguintes forem satisfeitas $\mathbf{r}(a)$ existe $\displaystyle \lim_{t \to a}\, \mathbf{r}(t)$ existe. $\displaystyle \lim_{t \to a}\, \mathbf{r}(t) = \mathbf{r}(a)$

Representação paramétrica de algumas curvas

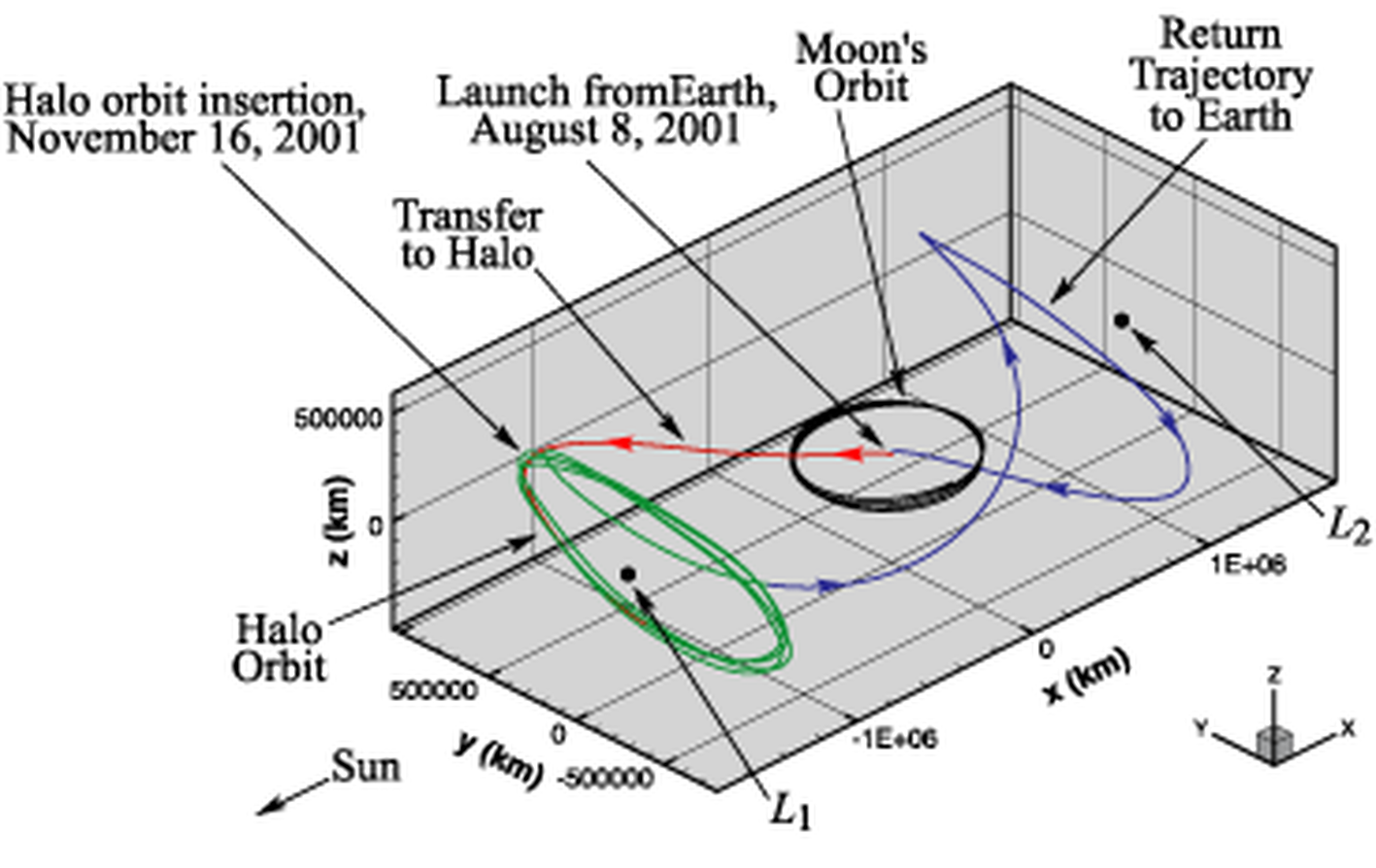
Utilizando o conceito de funções vetoriais podemos definir o que entendemos por uma curva. por curva entendemos o lugar geométrico de todos os pontos $P$ que tem por vetor posição \[ \mathbf{r}(t) = x(t)\,\mathbf{i} + y(t) \,\mathbf{j} + z(t) \,\mathbf{k} \nonumber \] onde supomos que $r(t)$ é uma função vetorial contínua. Do ponto de vista da Física, se $r(t)$ é a posição de uma partícula, então a curva representa sua trajetória no espaço. Existem as mais diversas possibilidades de curvas algumas tão complexas quanto a trajetória seguida pelo satélite Gênesis e é por esta razão que estas são classificas:

1. Curva plana: aquelas que estas contida num plano no espaço.
2. Curvas reversas: aquelas que não são planas
3. Curvas fechadas: são aquelas curvas que parametrizadas por $\mathbf{r}(t)$ com $t \in [a,b]$ se verifica que $\mathbf{r}(a) = \mathbf{r}(b)$
4. Curvas simples: aquelas que são definidas por um único valor do parâmetro $t$, excepto quando $t=a$ e $t=b$).

A continuação veremos a parametrização de algumas curvas

Parametrização de uma reta

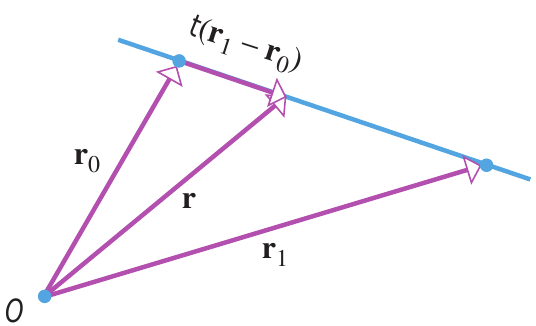
A parametrização de uma recta está dada por \[ \mathbf{r}(t) = \mathbf{a} + t\, \mathbf{b} \label{eqreta} \] Observe que está é simplesmente a equação da reta, dessa forma o vetor $\mathbf{a}$ aponta para um ponto qualquer pelo qual a reta passa e o vetor $\mathbf{b}$ é um vetor que está ao longo da reta.

Um caso particularmente interessante é quando são conhecido os vetores que aponta a 2 pontos sobre a reta, nesses casos o vetor $\mathbf{b}$ na equação \ref{eqreta} está dado por $\mathbf{b} = \mathbf{r}_1 - \mathbf{r}_0$, de forma que \[ \mathbf{r}(t) = \mathbf{r}_0 + t\, \left( \mathbf{r}_1 - \mathbf{r}_0 \right) \label{eqreta2} \] ou, manipulando algebricamente \[ \mathbf{r}(t) = \left( 1 - t \right)\mathbf{r}_0 + t\,\mathbf{r_1} \label{eqreta3} \]

Exemplo

Determinar uma representação paramétrica da reta que passa por $(2,-1,-1)$ na direção do vetor $\mathbf{b}(t) = (2,-3,1)$

SOL.
Como $\mathbf{a} = (2,-1,-1)$, então \[ \begin{align*} \mathbf{r}(t) =& \mathbf{a} + t\, \mathbf{b}\\ =& (2+2t),\mathbf{i} + (1-3t) \,\mathbf{j}+(-1+t) \,\mathbf{k} \end{align*} \]

Parametrização de uma circunferência

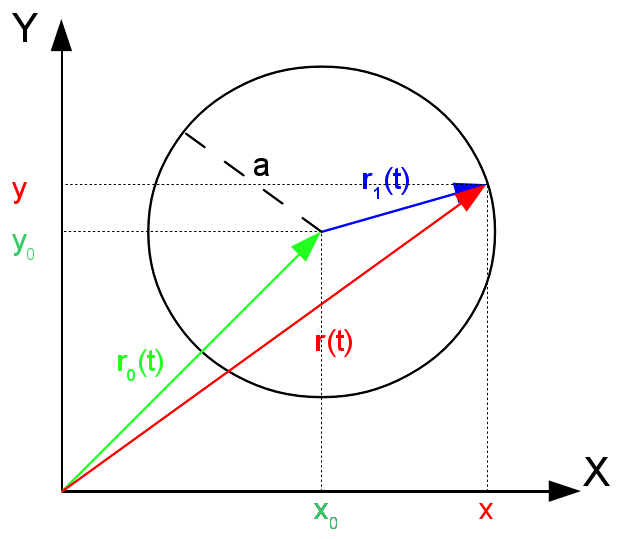
Vamos partir do caso mais geral e dele ao mais simples, isto é, vamos supor que a circunferência está centrada num ponto $\left(x_0,y_0\right)$, como mostra a figura a seguir

Da figura resulta obvio que o vetor posição $\mathbf{r}(t)$ resulta da soma de dois vetores \[ \mathbf{r}(t) = \mathbf{r}_0(t) + \mathbf{r}_1(t) \] o primeiro vetor aponta para a origem (e por tanto é fixo) e o segundo vetor aponta da origem para qualquer ponto na circunferência. Se o raio da circunferência é $a$ então a coordenada do ponto na circunferência, relativo à origem, está dado por \[ \begin{align*} x_1 =& a \cos t\\ y_1 =& a \sin t \end{align*} \] de forma que \[ \mathbf{r}_1(t) = a \cos t \,\mathbf{i} + a \sin t \,\mathbf{j}\;\;\;\;\;0\leq t \leq 2\pi \nonumber \] se a posição da origem está dada por \[ \mathbf{r}_0(t) = x_0 \,\mathbf{i} + y_0 \,\mathbf{j} \nonumber \] teremos que \[ \mathbf{r}(t) = \left( x_0 + a \cos t \right) \,\mathbf{i} + \left( y_0 + a \sin t \right)\,\mathbf{j}\;\;\;\;\;0\leq t \leq 2\pi \label{circunferencia} \] Quando a circunferência está na origem a equação reduz para \[ \mathbf{r}(t) = a \cos t \,\mathbf{i} + a \sin t\,\mathbf{j}\;\;\;\;\;0\leq t \leq 2\pi \label{circunferenciaorigem} \]

Exemplo

Obter a equação paramétrica da circunferência $x^2+y^2-6x-4y+4=0$ no plano $z=3$

SOL.
Primeiro vamos determinar o centro da circunferência, para isso completamos quadrado \[ \begin{align*} -6x+9+y^{2}-4y+4=&9\\ \left( x-3\right) ^{2}+\left( y-2\right) ^{2}=&9 \end{align*} \] de forma que o centro está em $\left( 3,2\right)$, por tanto \[ \mathbf{r}(t) = \left( 3 + \cos t \right) \,\mathbf{i} + \left( 2 + 3\sin t \right)\,\mathbf{j} + 3 \,\mathbf{k} \nonumber \]

Parametrização de uma elipse

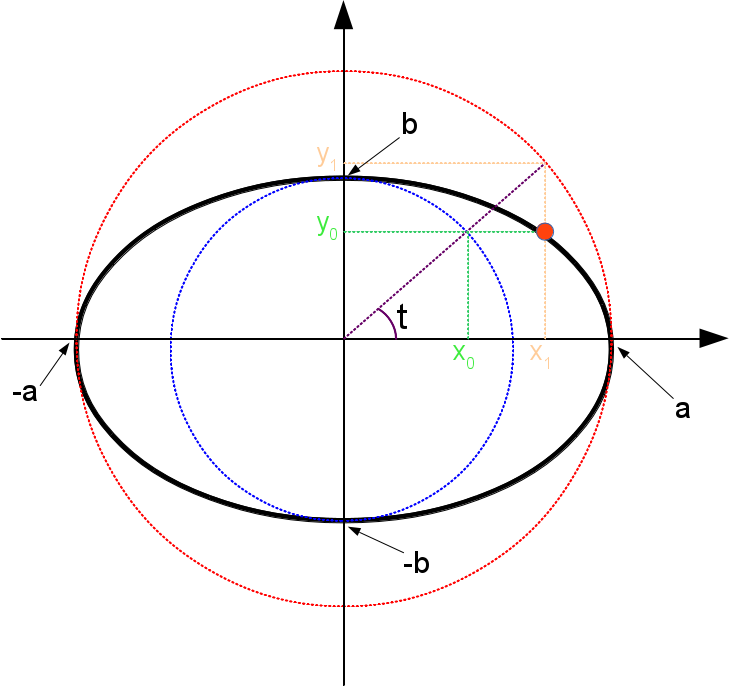
Dada a complexidade da elipse, vamos parametrizar primeiro ela supondo que está na origem, depois estenderemos para o caso quando ela estiver fora da origem.

O nosso objetivo é calcular a posição de cada um dos pontos sobre a elipse, suponhamos por exemplo o ponto em laranja sobre a elipse em preto mostrada na figura acima. Note que a posição em $x$ do ponto corresponde exatamente à posição $x_1$ e a posição em $y$ corresponde a posição $y_0$, assim \[ \begin{align*} x_1 =& a \cos t\\ y_1 =& b \sin t \end{align*} \] dessa forma, o vetor posição estará dado por \[ \mathbf{r}(t) = a \cos t \,\mathbf{i} + b \sin t \,\mathbf{j};\;\;\;\;0\leq t \leq 2\pi \label{elipseorigem} \] seguindo uma metodologia similar à utilizada para o caso da circunferência fora da origem devemos esperar que \[ \mathbf{r}(t) = \left(x_0 + a \cos t \right) \,\mathbf{i} + \left(y_0 + b \sin t \right) \,\mathbf{j};\;\;\;\;0\leq t \leq 2\pi \label{elipse} \] onde $\left(x_0,\,y_0 \right)$ é a posição do centro da elipse (nova origem).

É interessante lembrar que a equação cartesiana de uma elipse está dada por \[ \dfrac{\left( x-x_0 \right)^2}{a^2} + \dfrac{\left( y - y_0\right)^2}{b^2} = 1 \nonumber \] sendo $\left(x_0,\,y_0 \right)$ é a posição do centro da elipse, $a$ e $b$

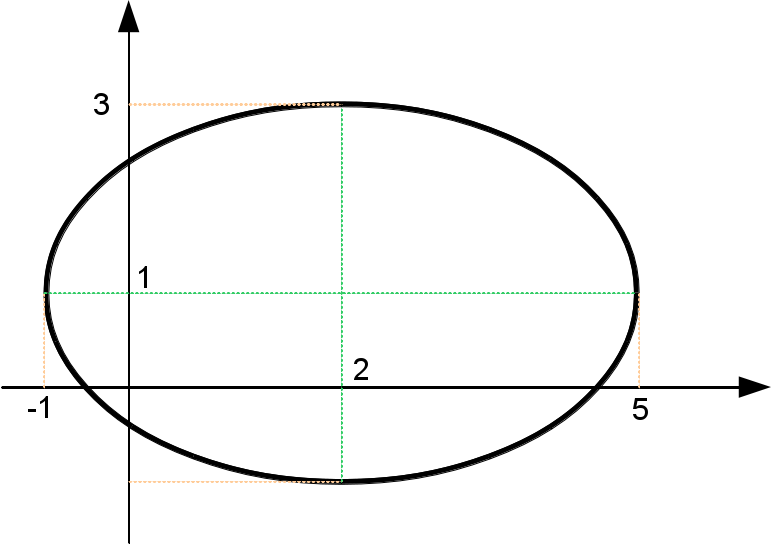
Exemplo

Dada a elipse acima, encontre sua equação vetorial
SOL.
Da figura vemos que o centro da elipse está em $\mathbf{r}r =\left(2,1 \right)$. O comprimento do semi-eixo maior é $5-2=3$ e do semi eixo menor é $3-1 = 2$, de forma que \[ \left(\dfrac {x-2} {3}\right)^{2}-\left( \dfrac {y-1} {2}\right) ^{2}=1 \nonumber \] de onde a equação vetorial é \[ \mathbf{r}(t) = \,\left(2+3\cos t \right)\mathbf{i} + \left(1 + 2 \sin t \right) \,\mathbf{j} \nonumber \]

Exemplo

Escreva a equação vetorial para a elipse $9x^{2}+4y^{2}=36$ no plano $xy$
SOL.
\[ \begin{align*} 9x^{2}+4y^{2}=&36\\ \dfrac {x^{2}} {4}+\dfrac {y^{2}} {9}=&1\\ \left( \dfrac {x} {2}\right) ^{2}+\left( \dfrac {y} {3}\right) ^{2}=&1 \end{align*} \] de onde \[ \mathbf{r}(t) = \,\left(2\cos t \right)\mathbf{i} + \left(3 \sin t \right) \,\mathbf{j} \nonumber \]

Exemplo

Dada a elipse acima, encontre sua equação vetorial
SOL.
Da figura vemos que o centro da elipse está em $\mathbf{r}r =\left(2,1 \right)$. O comprimento do semi-eixo maior é $5-2=3$ e do semi eixo menor é $3-1 = 2$, de forma que \[ \left(\dfrac {x-2} {3}\right)^{2}-\left( \dfrac {y-1} {2}\right) ^{2}=1 \nonumber \] de onde a equação vetorial é \[ \mathbf{r}(t) = \,\left(2+3\cos t \right)\mathbf{i} + \left(1 + 2 \sin t \right) \,\mathbf{j} \nonumber \]