Derivada
| Definição |
|
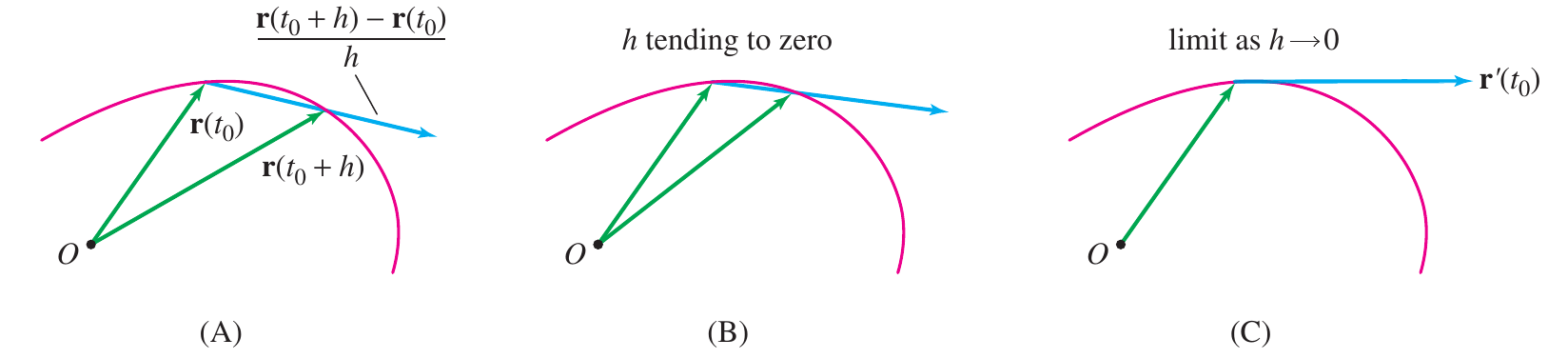
Se $\mathbf{r}(t)$ é uma função vetorial, definimos a derivada de $\mathbf{r}(t)$ em relação a $t$ como uma função vetorial $\mathbf{r}'(t)$ dada por \[ \mathbf{r}'(t) =\lim _{h\rightarrow 0} \dfrac{\mathbf{r}(t+h) - \mathbf{r}(t)}{h} \] O domínio da função resultante coincide com o domínio da função original. |
Se aplicarmos a definição acima a uma função vetorial, obteremos facilmente o próximo teorema
| Teorema |
|
Se $\mathbf{r}(t)$ é uma função vetorial, então $\mathbf{r}(t)$ é diferenciável em relação a $t$ se e somente se suas componente são diferenciáveis em relação a $t$, de forma que as componente de $\mathbf{r}'(t)$ são as derivadas das componentes de $\mathbf{r}(t)$. |
Similarmente a como visto em cálculo I, aplicar a definição para realizar o computo da derivada pode ser uma tarefa complexa dependendo da forma funcional da função vetorial, por tanto resulta interessante calcular, a partir da definição, as regras de diferenciação
| Regras de diferenciação |
|
Se $\mathbf{r}(t)$, $\mathbf{r}_1(t)$ e $\mathbf{r}_2(t)$ 3 funções vetoriais, que podem estar definidas em um espaço 3D ou 2D, e seja $f(t)$ uma função real diferenciável, $m$ um escalar e $\mathbf{c}$ um vetor constante, então as seguintes regras de diferenciação permanecem válidas:
|
Exemplo 01
Cálcule a derivada do vetor $\mathbf{r}(t)=\left< 2+\sin\,t,\, \cos \, t,\, t^2 \right> $
Exemplo 02
Cálcule a derivada do vetor $\mathbf{r}(t)=\left< 2+\sin\,t,\, \cos \, t,\, t^2 \right>$
Interpretação Geométrica da derivada de uma função vetorial
Geometricamente o vetor derivada é um vetor que é tangente à trajetória descrita pelo vetor $\mathbf{r}(t)$, ou seja, tangente à curva.
Isto é evidente quando funções vetoriais são utilizadas por físicos. Um exemplo é utilizar $\mathbf{r}(t)$ como a posição da partículas em todo instante $t$, a derivada deste vetor nos dá a velocidade $\mathbf{v}(t)$ e a derivada do vetor velocidade nos da a aceleração $\mathbf{a}(t)$, um vetor perpendicular a outro.
Exemplo 03
Encontre o vetor velocidade e aceleração de uma partícula que se move ao longo da curva $C$ descrita por $\mathbf{r}(t) = 2\sin \,\dfrac{1}{2}t \,\mathbf{i} + \cos \,\dfrac{1}{2}t \,\mathbf{j}$
Exemplo 04
O vetor posição de uma partícula em movimento no plano está dado por
\[
\mathbf{r}(t) = t \,\mathbf{i} + \dfrac{1}{t+1} \,\mathbf{j},\;\;\;\;\; t \geq 0
\nonumber
\]
(a) Determinar o vetor velocidade e o vetor aceleração, para qualquer $t$
(b) Esboçar a trajetória desenhando os vetores velocidade nos tempos $t=0$ e $t=1$.
A partir do exemplo anterior vemos que as funções vetoriais também são passiveis de serem derivadas de forma sucessiva, assim a aceleração é a II derivada da posição.
Podemos estender este conceito geométrico além, como se mostra na próxima definição
| Definição de vetor tangente |
|
Seja $P$ um ponto no gráfico de uma função vetorial $\mathbf{r}(t)$ o qual é localizado desde um ponto origem $O$ pelo vetor $\mathbf{r}\left(t_0 \right)$. Se $\mathbf{r}'\left(t_0 \right)$ existe e $\mathbf{r}'\left(t_0 \right) \neq 0$, então chamaremos $\mathbf{r}'\left(t_0 \right)$ um vetor tangente ao gráfico de $\mathbf{r}\left(t \right)$ em $\mathbf{r}\left(t_0 \right)$, e à linha que passa pelo ponto $P$ que é paralela ao vetor tangente chamaremos de linha tangente ao gráfico de $\mathbf{r}\left(t \right)$ em $\mathbf{r}\left(t_0 \right)$. |
Exemplo 05
Encontre a equação paramétrica da linha tangente à hélice circular \[ \begin{align*} x =& \cos t\\ y =& \sin t\\ z =& t \end{align*} \] onde $t=t_0$. Utilize esse resultado para determinar a equação paramétrica da reta que passa por $t=\pi$
Exemplo 06
Mostre que $\mathbf{r}'(t)$ é ortogonal a $\mathbf{r}(t)$ sempre que $\left| \mathbf{r}(t) \right|$ seja uma constante
Curvas Suaves
| Definição |
|
Dizemos que uma curva representada por $\mathbf{r}(t)$ é uma curva ou função suave de $t$ se $\mathbf{r}'(t)$ é continua e $\mathbf{r}'(t)\neq 0$ para toda valor de $t$. |
Geometricamente estas curvas se caraterizam por não terem pontos angulosos. Também definimos o fato de que a curva pode ser suave por partes.
Exemplo 07
Determine se as seguintes funções são suaves
- $\displaystyle \mathbf{r}(t) = a\cos t \,\mathbf{i} + a \sin t \,\mathbf{j} + ct \,\mathbf{k}\;\;\;\;\;\; (a>0, c>0)$
- $\displaystyle \mathbf{r}(t) = t^2 \,\mathbf{i} + t^3 \,\mathbf{j}$
Curvas orientadas
Uma curva orientada é uma curva onde uma direção consistente é definida ao longo da curva. Definir uma direção em cada ponto significa escolher um dos dois vetores tangente que podem ser definidos em aquele ponto.
Mas como a escolha de uma orientação definida como positiva é arbitraria, nos seguiremos a seguinte escolha, consideraremos que a curva $C$, definida por \[ \mathbf{r}^{-}(t) = x(t)\,\mathbf{i} +y(t) \,\mathbf{j} +z(t) \,\mathbf{k}\;\;\;\;t\in[a,b] \nonumber \] positivamente orientada quando o percurso resulta do incremento dos valores do parâmetro.
A curva com orientação oposta, $-C$, se define como \[ \begin{align*} \mathbf{r}{r}^-(t) =& \mathbf{r}{r}(a+b-t)\\ =&x(a+b-t)\,\mathbf{i} +y(a+b-t) \,\mathbf{j} +z(a+b-t) \,\mathbf{k}\;\;\;\;t\in[a,b] \end{align*} \nonumber \]
exemplo 08
Parametrizar a circunferência de centro na origem e raio $a$ no sentido anti horário.
exemplo 09
Parametrizar o segmento de reta que passa pelos pontos $A(0,0,1)$ e $B(1,2,3)$. Repita o procedimento anterior considerando uma orientação oposta.
Conceito de Integral com funções vetoriais
Integrais definidas
Se $\mathbf{r}(t)$ é uma função vetorial que é continua no intervalo $a\leq t \leq b$ podemos definir a integral definida de $\mathbf{r}(t)$ sobre este intervalo como o limite da somas de Riemann da mesma forma que são definidas para o caso das funções em $\mathbb{R}$. Especificamente se define \[ \int_a^b \mathbf{r}(t)\,dt = \lim_{max\,\Delta t_k \rightarrow 0} \;\sum_{k=1}^{n} \mathbf{r}(t^*_k)\, \Delta t_k \nonumber \] aplicando essa definição às componente do vetor \[ \begin{eqnarray*} \int_a^b \mathbf{r}(t)\,dt &=& \lim_{max\,\Delta t_l \rightarrow 0} \;\sum_{l=1}^{n} \mathbf{r}(t^*_l)\, \Delta t_l \nonumber\\ &=& \lim_{max\,\Delta t_l \rightarrow 0} \left[ \left( \sum_{l=1}^{n} f(t^*_l)\, \Delta t_l \right)\,\mathbf{i} + \left( \sum_{l=1}^{n} g(t^*_l)\, \Delta t_l\right)\,\mathbf{j} + \left( \sum_{l=1}^{n} h(t^*_l)\, \Delta t_l\right)\,\mathbf{k} \right] \end{eqnarray*} \] e \[ \int_a^b \mathbf{r}(t)\,dt = \left( \int_a^b f(t)\,dt \right)\,\mathbf{i}+ \left( \int_a^b g(t)\,dt\right) \,\mathbf{j} + \left( \int_a^b h(t)\,dt\right) \,\mathbf{k} \]
Exemplo 10
Seja $\mathbf{r}(t) = t^2\mathbf{i} + e^t\mathbf{j} - \left( 2\cos \pi t \right)\mathbf{k}$ calcule a integral entre $[0, 1]$
Podemos provar que todas as regras de integração que são válidas para funções em $\mathbb{R}$ se mantem válidas para as funções vetoriais.
Integrais indefinidas
A antiderivada de uma função vetorial $\mathbf{r}(t)$ é uma função vetorial $\mathbf{R}(t)$ tal que \[ \mathbf{R}'(t) = \mathbf{r}(t) \nonumber \] isto é \[ \int \mathbf{r}(t)\, dt = \mathbf{R}(t) + \mathbf{C} \] onde $\mathbf{C}$ é um vetor constante arbitrário.
Exemplo 11
Encontre $\mathbf{r}(t)$ sabendo que $\mathbf{r}'(t) = \left< 3, 2t \right>$ e que $\mathbf{r}(1) = \left< 2, 5 \right>$