Rotacional
Assim como a divergência está relacionada à continuidade (criação ou destruição de campo) existe uma outra operação que nos indica se um determinado campo tem algum tipo de rotação, a essa operação chamamos de rotacional
| Definição |
|
Suponhamos que $\mathbf{F}:U\subseteq \mathbb{R}^3 \to \mathbb{R}^3$, $F=(F_x,F_y,F_z)$, diferenciável, definido no conjunto aberto $U$ de $\mathbb{R}^3$. Se define o rotacional de $\mathbf{F}$ no ponto $P$ de $U$, denotado por $\nabla \times \mathbf{F}(p)$, como \[ \nabla \times \mathbf{F}(p) = \left( \dfrac{\partial F_z}{\partial y}-\dfrac{\partial F_y}{\partial z}, \dfrac{\partial F_x}{\partial z}-\dfrac{\partial F_z}{\partial x}, \dfrac{\partial F_y}{\partial x}-\dfrac{\partial F_x}{\partial y}\right) \nonumber \] onde as derivas parciais das funções componentes de $\mathbf{F}$ são avaliadas no ponto $P$. |
Note que $\nabla \times \mathbf{F}(p)$ é um vetor por tanto podemos falar do "campo rotacional" de $\mathbf{F}$, $\nabla \times \mathbf{F}(p):U\subseteq \mathbb{R}^3 \to \mathbb{R}^3$, onde cada ponto $p\in U$ associa um vetor $\nabla \times \mathbf{F}(p) \in \mathbb{R}^3$
Uma forma simples de recordar a equação do rotacional é utilizando \[ \begin{align*} \nabla \times \mathbf{F} =& det \;\begin{bmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial \;}{\partial x} & \dfrac{\partial \;}{\partial y} & \dfrac{\partial \;}{\partial z}\\ F_x & F_y & F_z \end{bmatrix}\\ =& \left( \dfrac{\partial F_z}{\partial y}-\dfrac{\partial F_y}{\partial z} \right) \,\mathbf{i} - \left( \dfrac{\partial F_z}{\partial x} - \dfrac{\partial F_x}{\partial z} \right) \,\mathbf{j} + \left( \dfrac{\partial F_y}{\partial x}-\dfrac{\partial F_x}{\partial y}\right) \,\mathbf{k} \end{align*} \]
Quando introduzimos o conceito de rotacional nos dizemos que essa operação mede algum tipo de rotação do campo. Essa definição ficou ambígua devido a que o conceito de rotacional não é obvio
Consideremos a figura acima, do lado esquerdo tem um graveto sob uma corrente de água o qual se desloca mantendo exatamente a mesma posição. Acontece que o rotacional dessa situação é zero diferentemente do caso onde o graveto rota a medida que se desloca. Campos que verificam $\nabla \times \mathbf{F} = 0$ são ditos de irrotacionais.
| Teorema |
|
Para qualquer campo vetorial $\mathbf{F}$ de classe $C^2$, \[ \vec{\nabla} \cdot \left(\vec{\nabla} \times \mathbf{F} \right) = 0 \nonumber \] ou seja, a divergência de qualquer rotacional é zero. |
Interpretação física
Parece ser obvio que como o rotacional mede a rotação de alguma forma ele deve estar relacionado com o movimento angular, mas como veremos a continuação não é uma relação obvia.
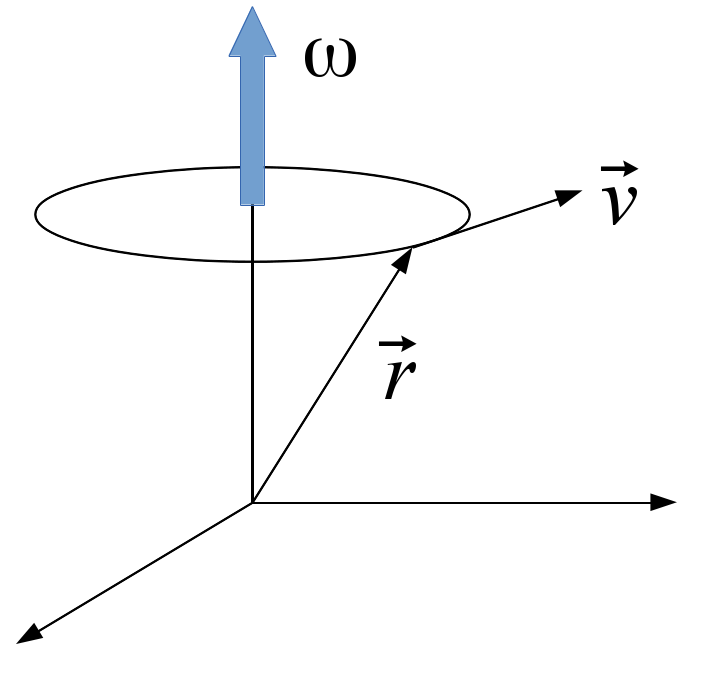
Suponha um corpo que gira em torno de eixo que passa pela origem do sistema de coordenadas, com vetor angular $\displaystyle \mathbf{\omega}$. Seja $\displaystyle \mathbf{v}$ o vetor velocidade num ponto $P$ do corpo, vamos calcular $\displaystyle \nabla \times \mathbf{v}$
Seja $\displaystyle \mathbf{\omega} = \left( \omega_1, \omega_2, \omega_3\right)$ e $\displaystyle \mathbf{r} = \left( x, y, z\right)$, dessa forma \[ \mathbf{v}= \mathbf{\omega} \times \mathbf{r} \nonumber \] de onde \[ \mathbf{v} = \left( \omega_2 z - \omega_3 y \right) \,\mathbf{i} + \left( \omega_3 x - \omega_1 z \right) \,\mathbf{j} + \left( \omega_1 y - \omega_2 x \right) \,\mathbf{k} \nonumber \] agora vamos calcular $\displaystyle \nabla \times \mathbf{v}$: \[ \begin{align*} \nabla \times \mathbf{v} =& det \;\begin{bmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \dfrac{\partial \;}{\partial x} & \dfrac{\partial \;}{\partial y} & \dfrac{\partial \;}{\partial z}\\ \left( \omega_2 z - \omega_3 y \right) & \left( \omega_3 x - \omega_1 z \right) & \left( \omega_1 y - \omega_2 x \right) \end{bmatrix}\\ =& \left( \dfrac{\partial \left( \omega_1 y - \omega_2 x \right)}{\partial y}-\dfrac{\partial \left( \omega_3 x - \omega_1 z \right)}{\partial z} \right) \,\mathbf{i} - \left( \dfrac{\partial \left( \omega_1 y - \omega_2 x \right)}{\partial x} - \dfrac{\partial \left( \omega_2 z - \omega_3 y \right)}{\partial z} \right) \,\mathbf{j} +\\ & \left( \dfrac{\partial \left( \omega_3 x - \omega_1 z \right)}{\partial x}-\dfrac{\partial \left( \omega_2 z - \omega_3 y \right)}{\partial y}\right) \,\mathbf{k}\\ =& \left( \omega_1 + \omega_1 \right) \,\mathbf{i} - \left( - \omega_2 - \omega_2 \right) \,\mathbf{j} + \left( \omega_3 + \omega_3 \right) \,\mathbf{k} \\ =& 2\omega_1 \,\mathbf{i} + 2\omega_2 \,\mathbf{j} + 2\omega_3 \,\mathbf{k}\\ =& 2 \vec{\omega} \end{align*} \] Ou seja, o rotacional nos devolve o dobro da velocidade angular
Exemplo
Calcule o campo rotacional das seguintes funções
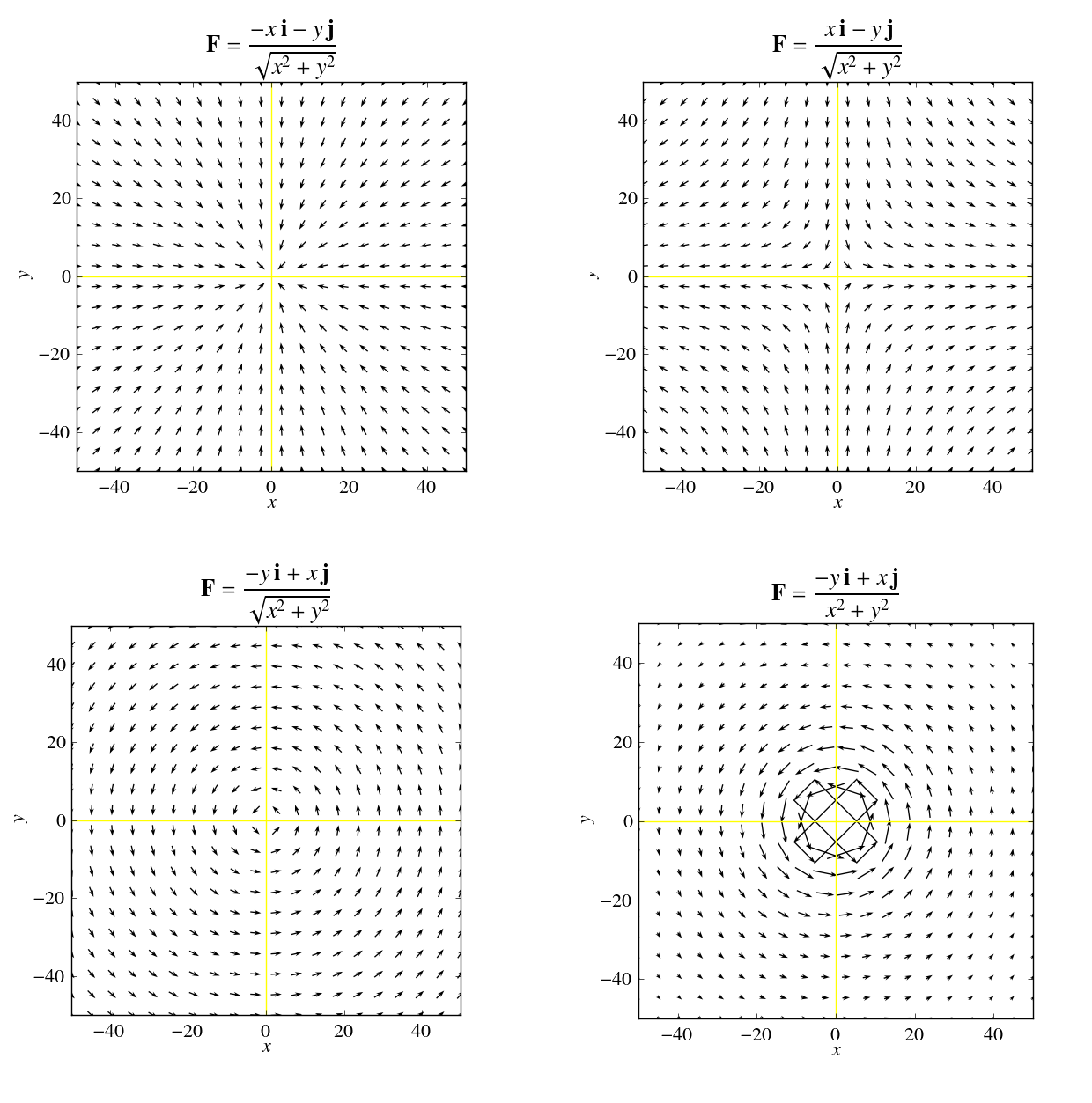
1. $\displaystyle \mathbf{F} = \dfrac{-x\,\mathbf{i} - y \,\mathbf{j}}{\sqrt{x^2+y^2}}$
2. $\displaystyle \mathbf{F} = \dfrac{-y\,\mathbf{i} + x \,\mathbf{j}}{\sqrt{x^2+y^2}}$
3. $\displaystyle \mathbf{F} = \dfrac{-y\,\mathbf{i} + x \,\mathbf{j}}{x^2+y^2}$
4. $\displaystyle \mathbf{F} = \dfrac{x\,\mathbf{i} -y \,\mathbf{j}}{\sqrt{x^2+y^2}}$
5. Um escoamento é representado pelo campo de velocidades $\displaystyle \mathbf{v} = 10x\,\mathbf{i} - 10y \,\mathbf{j} + 30 \,\mathbf{k}$, verifique (a) Se há um escoamento incompressível. (b) Se há um escoamento irrotacional.
6. Para um escoamento no plano $xy$, a componente $y$ da velocidade é dado por $v_y = y^2-2x+2y$, determine uma possível componente em $x$ para um escoamento incompressível.
7. Mostre que o campo vetorial $\displaystyle \mathbf{V}(x,y,z) = x \,\mathbf{i} + y \,\mathbf{j} + z \,\mathbf{k}$ não pode ser o rotacional de algum campo vetorial $\mathbf{F}$, isto é $\mathbf{V} = \vec{\nabla} \times \mathbf{F}$.
Campos conservativos
| Definição |
|
Para qualquer função $f$, o campo vetorial $\mathbf{F} = \nabla f$ é chamado do campo gradiente da função $f$ enquanto que a função $f$ é chamada de função potencial para $\mathbf{F}$. Se existe um $f$ tal que $\mathbf{F} = \nabla f$, então diremos que o campo vetorial $\mathbf{F}$ é um campo vetorial conservativo. |
A partir dessa definição podemos estabelecer alguns resultados:
- Se um campo vetorial $\mathbf{F}=(F_x, F_y,F_z)$ é conservativo, se verifica que \[ \begin{align*} \dfrac{\partial F_x}{\partial y} =& \dfrac{\partial F_y}{\partial x}\\ \dfrac{\partial F_y}{\partial z} =& \dfrac{\partial F_z}{\partial y}\\ \dfrac{\partial F_z}{\partial x} =& \dfrac{\partial F_x}{\partial z}\\ \end{align*} \]
- Se $\mathbf{F}$ é conservativo, então duas funções potenciais de $\mathbf{F}$ são iguais entre sim a menos de uma constante
| Teorema |
|
Para qualquer função de clase $C^2$, \[ \vec{\nabla} \times \left(\vec{\nabla} f \right)= \mathbf{0} \nonumber \] ou seja, o rotacional de qualquer gradiente é o vetor zero |
A propriedade a tem que ser bem entendida, todo campo conservativo tem seu rotacional igual a zero, mas nem todo campo com rotacional igual a zero é um campo conservativo necessariamente. Somente aqueles campos vetoriais definidos num domínio simplesmente conexo e cujo rotacional é igual a zero são ditos de conservativos
| Definição |
|
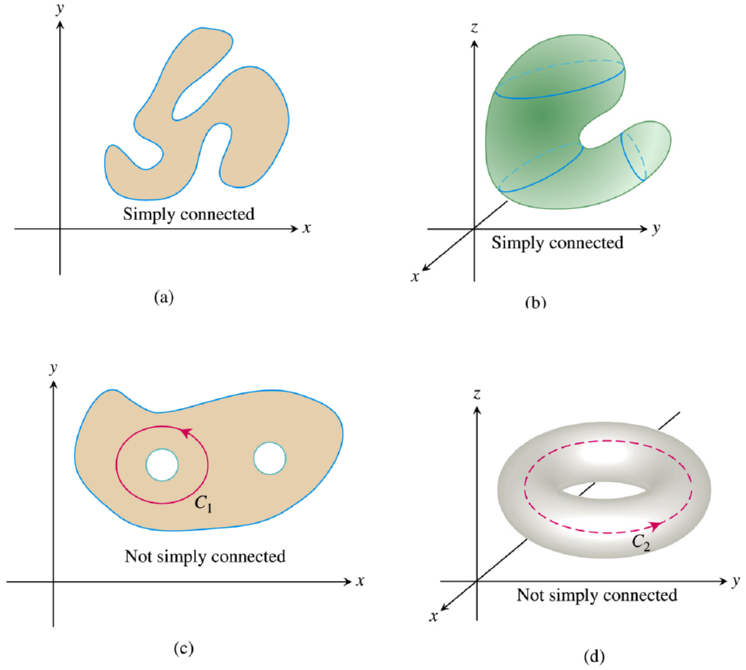
Uma região $R$ em $\mathbb{R}^2$ ou $\mathbb{R}^3$ é simplesmente conexa se consiste em uma única peça simples conectada e se qualquer curva $C$ simples e fechada em $R$ pode ser continuamente reduzida a um ponto, mantendo-se em $R$ durante a deformação. |
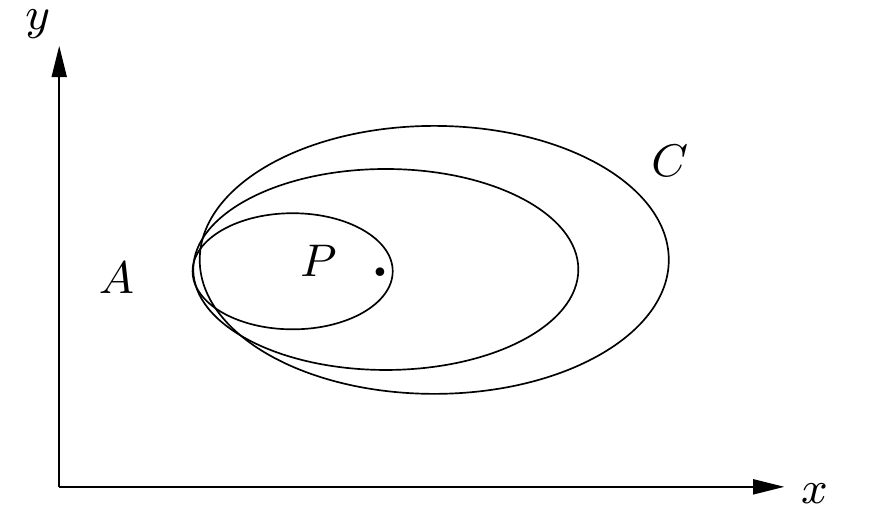
Basicamente o que essa definição quer dizer é que a região $R$ não possui buracos.
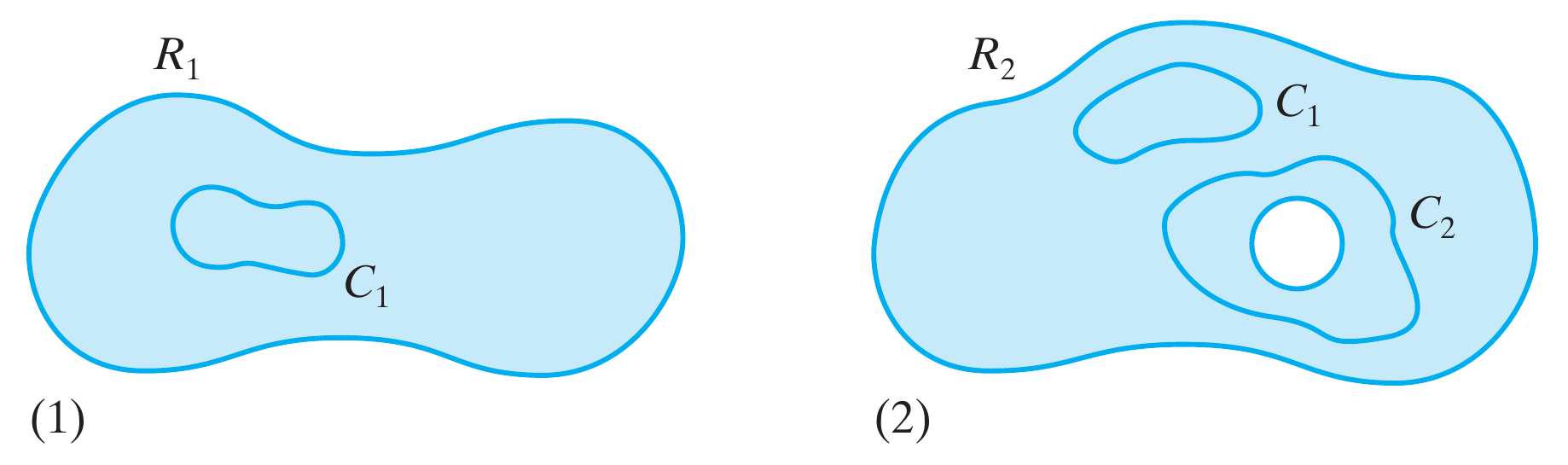
Assim a região $R_1$ na figura acima é simplesmente conexa mas $R_2$ não é, mesmo que há regiões como a encerradas pela curva $C_1$ que seriam simplesmente conexas, existe um buraco encerrado por $C_2$, mas a região é dita conexa (mas não simples)
A definição sobre não possuir buracos dentro do domínio da função não é obvia por exemplo no caso de funções definidas em $\mathbb{R}^2$ se temos um só ponto fora do domínio é suficiente para que a função não seja simplesmente conexa como no caso de $f(x) = 1/\left(x^2+y^2\right)$ que não está definida na origem. No caso de $\mathbb{R}^3$, o espaço pode ter singularidades dentro de seu domínio e se manter como sendo simplesmente conexa
| Definição |
|
Suponha um campo definido em $\mathbb{R}^n$, onde $n \geq 0$, mesmo que a função não este definida num conjunto finito $x_1, x_2, \ldots, x_m$, ela continuara a ser simplesmente conexa. |
A razão para isto é até obvia, no caso de uma singularidade dentro de $\mathbb{R}$ e $\mathbb{R}^2$, não há forma de escapar dela deformando a curva continuamente, sempre estaremos pressos ao plano onde está contido o ponto
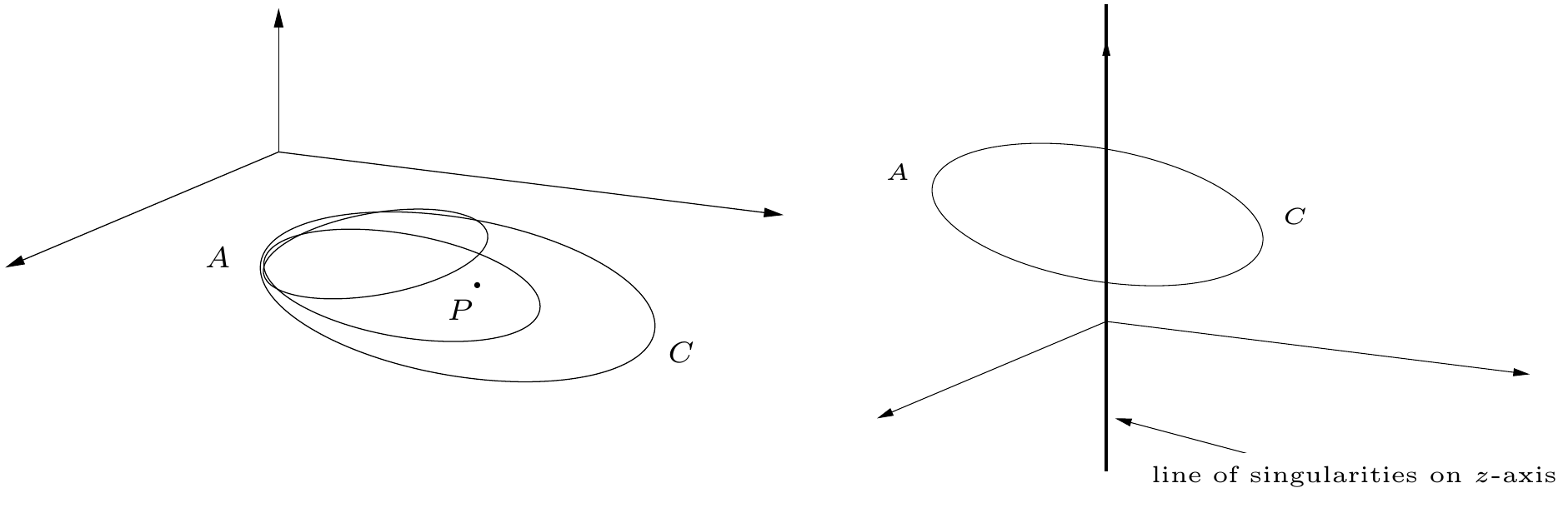
Mas para o caso de $\mathbb{R}^3$ você pode evitar os pontos simplesmente levantando a curva (o que não rompe ela, simplesmente deforma), isto é, você tem outra dimensão para escapar e assim evitar a singularidade e continuar deformando a curva até um ponto.
Como mostra a figura ao lado queremos que a curva $C$ seja deformada continuamente até o ponto $A$ e no plano se a curva engloba a singularidade $P$ não temos como chegar até $A$. É obvio que para o caso de $\mathbb{R}^3$ que um conjunto finito de pontos sempre poderão serem contornados mas uma linha não, como mostra a figura embaixo
Exemplo
- Seja $R=\left\{ (x,y)\, \left| \, 4 < x^2 + y^2 < 16 \right. \right\}$ é um domínio conexo mas não simples.
- O interior de uma esfera com um número finito de pontos é um domínio simplesmente conexo.
- O interior de um cubo onde foi removida uma diagonal não é uma região simplesmente conexa.
Entendido o que é uma região simplesmente conexa podemos estabelecer o seguinte teorema
| Teorema |
|
Seja $\mathbf{F}$ um campo vetorial de clase $C^1$ cujo domínio é uma região simplesmente conexa $R$ em $\mathbb{R}^2$ ou $\mathbb{R}^3$. Então $\mathbf{F} = \nabla f$ para alguma função escalar de clase $C^2$ em $R$ se o somente se $\vec{\nabla} \times \mathbf{F} = 0$ para todos os pontos de $R$. |
Exemplos
O que pode se afirmar sobre os campos vetoriais $\mathbf{F}$ em $R$
- $\displaystyle \mathbf{F} = 2x^2y \,\mathbf{i} + 5xz \,\mathbf{j} + x^2 y^2 \,\mathbf{k}$ em $R=\mathbb{R}^3$
- $\displaystyle \mathbf{F} =\left( 4xy + z \right) \,\mathbf{i} + 2x^2 \,\mathbf{j} + x \,\mathbf{k}$ em $R=\mathbb{R}^3$
- $\displaystyle \mathbf{F} = \dfrac{-y}{x^2 + y^2}\,\mathbf{i} + \dfrac{x}{x^2 + y^2} \,\mathbf{j}$ em $R_1 = \left\{ (x,\, y)\left| (x-3)^2 + y^2 < 1 \right. \right\}$ e $R_2 = \left\{ (x,\, y)\left| 1 < x^2 + y^2 < 16 \right. \right\}$
Exemplo
- Verificar se \[ \mathbf{F}(x,y,z) = \left( yz+2 \right)\,\mathbf{i} + \left( xz+1 \right) \,\mathbf{j} + \left( xy + 2z \right) \,\mathbf{k} \nonumber \] é um campo gradiente, em caso afirmativo encontre a função potencial.
- Se $\displaystyle \varphi = \dfrac{q}{r}$ e $\mathbf{E}=-\vec{\nabla} \varphi$, verifique que $\vec{\nabla} \times \mathbf{E} = 0$
- Considere o campo vetorial $\mathbf{F}$ em $\mathbb{R}^3$ definido por \[ \mathbf{F}(x,y,z) = y\,\mathbf{i} + \left( z\cos yz + x\right) \,\mathbf{j} + \left( y\cos yz \right)\,\mathbf{k} \nonumber \] mostre que $\mathbf{F}$ é irrotacional e encontre um potencial escalar
- A massa $M$ na origem de $\mathbb{R}^3$ exerce uma força sobre uma massa $m$ localizada em $\mathbf{r}=(x,y,z)$ com magnitude $\dfrac{GMm}{r^2}$ em direção à origem. Aqui, $G$ é a constante de gravitação, a qual depende da unidade de medida utilizada, e $r=|\, \mathbf{r} \, |=\sqrt{x^2 + y^2 + z^2}$. Como o vetor $-\dfrac{\mathbf{r}}{r}$ é o vetor unitário em direção à origem, então podemos escrever \[ \mathbf{F}(x,y,z) = -\dfrac{GMm \mathbf{r}}{r^3} \nonumber \] Mostre que $\mathbf{F}$ é irrotacional e encontre o potencial escalar para $\mathbf{F}$ (note que $D\left[\mathbf{F}\right] = \mathbb{R}^3-(0,0,0)$ pois $\mathbf{F}$ não está definido na origem, mas mesmo assim o domínio é simplesmente conexo).