Material Extra (não faz parte da disciplina = prova)

Tubos

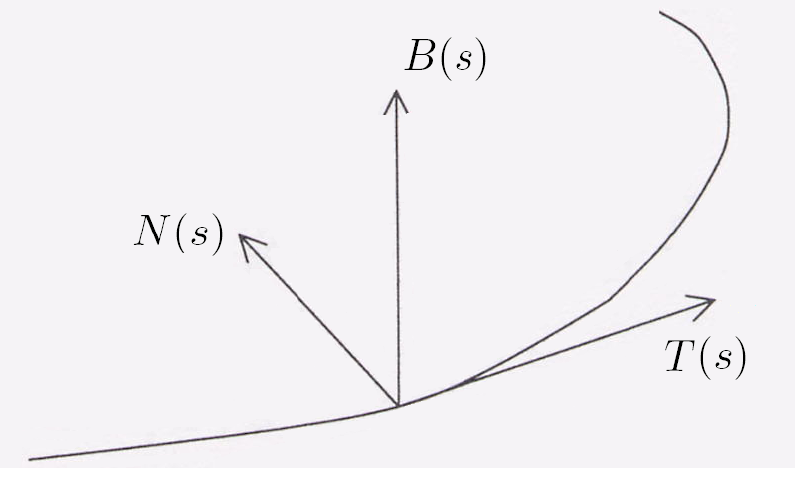
Seja $\mathbf{r}(u):A \subset \mathbb{R} \to \mathbb{R}^3$ uma curva a qual é parametrizada pelo comprimento de arco, para a qual existe um $r_0 > 0$ tal que $\kappa(s) < r_0^{-1}$ para qualquer $u \in A$. A circunferência \[ \mathbf{r}_c(v)=N(s)\,\cos\,v+B(s)\,\sin \, v \nonumber \] está no plano normal à curva em $\mathbf{r}(t)$, plano este perpendicular à tangente à curva em $\mathbf{r}(u)$. Quando a circunferência se move ao longo de $\mathbf{r}(u)$ define uma superfície, chamada de tubo de raio $a$ em torno de $\mathbf{r}(u)$, parametrizada por \[ \mathbf{r}_c(u,v)=\mathbf{r}(u) + a\left[N(s)\,\cos\,v+B(s)\,\sin \, v\right] \nonumber \] Onde $\kappa (s)$ é a curvatura definida como \[ \kappa (s) = \left|\, \mathbf{r}''(s) \, \right| \nonumber \] $\hat{N}(s)$ é o vetor normal definido como \[ \hat{N}(s) = \dfrac{\mathbf{T}'(s)}{\kappa (s)} \nonumber \] onde $\mathbf{T}(s)=\mathbf{r}'(s)=\dfrac{\mathbf{v}}{\left|\, \mathbf{v} \, \right|}$, $\hat{B}(s)$ é o vetor binormal definido como \[ \hat{B}(s) = \mathbf{T}(s) \times \hat{N}(s) \nonumber \] Esse três vetores forma o triedro de Frenet-Serret o qual é uma base ortonormal em cada ponto da curva.

Exemplo

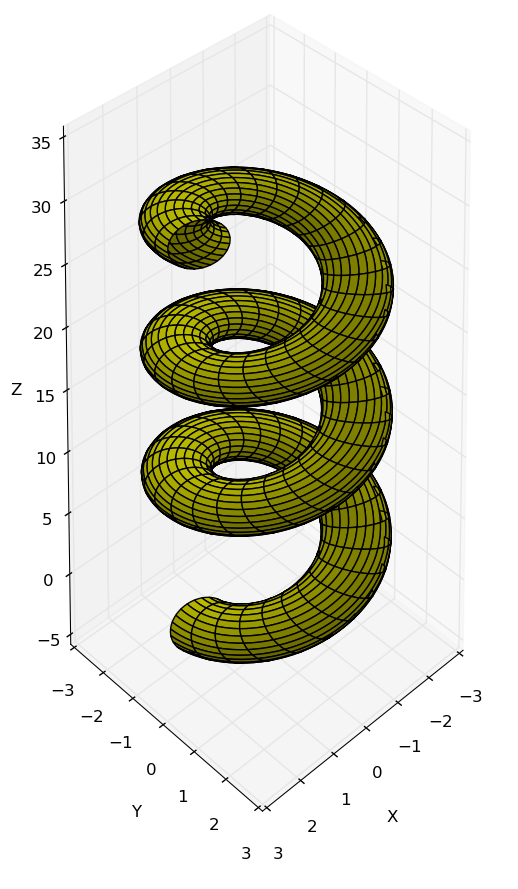
Encontre a representação vetorial do tubo helicoidal, para a hélice dada pela equação \[ \mathbf{r}(t) = 2\cos\,t\,\mathbf{i} + 2\sin\,t\,\mathbf{j} + \dfrac{5t}{3\pi} \,\mathbf{k} \nonumber \] Reparametrizando no comprimento \[ \begin{align*} \mathbf{r}'(t) =& -2\sin\,t\,\mathbf{i} + 2\cos\,t\,\mathbf{j} + \dfrac{5}{3\pi} \,\mathbf{k}\\ \left| \, \mathbf{r}'(t) \, \right| =& \sqrt{4 \sin^2\,t + 4 \cos^2\,t+\dfrac{25}{9\pi^2}}\\ =& \sqrt{4 +\dfrac{25}{9\pi^2}}\\ s(t) =& \int_0^t\,\sqrt{4 +\dfrac{25}{9\pi^2}}\,\,dt\\ s(t) =&\sqrt{4 +\dfrac{25}{9\pi^2}}\,\,t\\ t(s) =& \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}}\\ \mathbf{r}(s) =& 2\cos\, \left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right) \,\mathbf{i} + 2\sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{j} + \left( \dfrac{5\,s}{3\pi\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{k}\\ \mathbf{r}'(s) =& \dfrac{-2}{\sqrt{4 +\dfrac{25}{9\pi^2}}}\sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{i} + \dfrac{2}{\sqrt{4 +\dfrac{25}{9\pi^2}}}\cos\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{j} + \dfrac{5}{3\pi\sqrt{4 +\dfrac{25}{9\pi^2}}} \,\mathbf{k}\\ \mathbf{r}''(s) =& \dfrac{-2}{4 +\dfrac{25}{9\pi^2}}\cos\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{i} - \dfrac{2}{4 +\dfrac{25}{9\pi^2}}\sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{j}\\ \left|\, \mathbf{r}''(s) \, \right| =& \dfrac{-2}{4 +\dfrac{25}{9\pi^2}}\\ \mathbf{T}(s) =& \mathbf{r}'(s)\\ =&\dfrac{-2}{\sqrt{4 +\dfrac{25}{9\pi^2}}}\sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{i} + \dfrac{2}{\sqrt{4 +\dfrac{25}{9\pi^2}}}\cos\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{j} + \dfrac{5}{3\pi\sqrt{4 +\dfrac{25}{9\pi^2}}} \,\mathbf{k}\\ \mathbf{T}'(s) =& \dfrac{-2}{4 +\dfrac{25}{9\pi^2}}\cos\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{i} - \dfrac{2}{4 +\dfrac{25}{9\pi^2}}\sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{j}\\ \hat{\mathbf{N}}(s) =& \dfrac{\mathbf{T}'(s)}{\left|\, \mathbf{r}''(s) \, \right|}\\ =& -\cos\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{i} - \sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right)\,\mathbf{j}\\ \hat{\mathbf{B}}(s) = &\begin{bmatrix} \mathbf{i} & \,\mathbf{j} & \mathbf{k}\\ \dfrac{-2}{\sqrt{4 +\dfrac{25}{9\pi^2}}}\sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right) \;\;\;\;\;\;\;& \dfrac{2}{\sqrt{4 +\dfrac{25}{9\pi^2}}}\cos\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right) \;\;\;\;\;\;\;& \dfrac{5}{3\pi\sqrt{4 +\dfrac{25}{9\pi^2}}}\\ -\cos\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right) & -\sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right) & 0 \end{bmatrix}\\ = & \dfrac{5}{3\pi\sqrt{4 +\dfrac{25}{9\pi^2}}} \sin\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right) \,\mathbf{i} - \dfrac{5}{3\pi\sqrt{4 +\dfrac{25}{9\pi^2}}} \cos\,\left( \dfrac{s}{\sqrt{4 +\dfrac{25}{9\pi^2}}} \right) \,\mathbf{j} + \dfrac{2}{\sqrt{4 +\dfrac{25}{9\pi^2}}}\,\mathbf{k} \end{align*} \]