Comprimento do arco do ponto de vista vetorial
Continuando com o estudo da parametrização das curvas em $\mathbb{R}^3$ vamos estudar propriedades das curvas definidas por estas parametrizações tais como comprimento e curvatura. A área da matemática responsável pelo estudo de curvas e superfícies em dimensões superior (em inglés chamados de "manifolds") se denomina de geometria diferencial (muito utilizada no estudo da gravidade pelos Físicos).
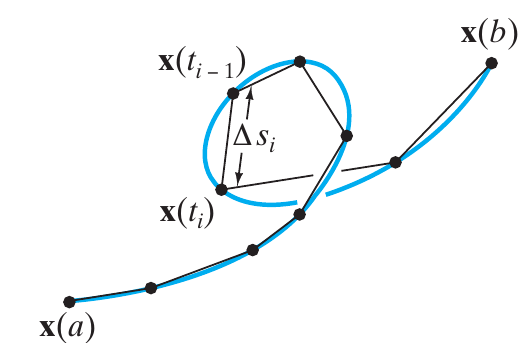
Seja $\mathbf{r}:[a,b] \rightarrow \mathbb{R}^3$ uma curva $C^1$ em $\mathbb{R}^3$. Vamos aproximar o comprimento $L$ de $\mathbf{r}$ da seguinte forma: primeiro, dividimos o intervalo $[a,b]$ em $n$ subintervalos, ou seja, escolhemos números $t_0, t_1, \ldots, t_n$ tais que $a=t_0 < t_1 < \ldots < t_n = b$. Seja $\Delta s_l$, onde $l=1, \ldots , n$, a distância entre $\mathbf{r}(t_{l-1})$ e $\mathbf{r}(t_{l})$ ao longo da curva, então podemos afirmar que \[ s \approx \sum _{l=1}^{n} \Delta s_l \nonumber \] sabendo que \[ \mathbf{r}(t) = x(t)\,\mathbf{i} + y(t) \,\mathbf{j} + z(t) \,\mathbf{k} \nonumber \] então, pelo teorema de Pitágoras \[ \Delta s_l = \sqrt{\Delta x^2 + \Delta y^2 + \Delta z^2} \nonumber \] onde $\Delta x = x(t_l) - x(t_{l-1})$, $\Delta y = y(t_l) - y(t_{l-1})$ e $\Delta z = z(t_l) - z(t_{l-1})$. Parece razoável ter a esperança de que a medida que $\Delta t_l = t_l - t_{l-1}$ se aproxime de zero, o valor de $\Delta s_l$ se aproxime mais e mais do valor do comprimento. Dessa forma definimos o comprimento $L$ de $\mathbf{r}$ como \[ s = \lim _{max\; \Delta t_l \rightarrow 0}\sum _{l=1}^{n} \sqrt{\Delta x^2 + \Delta y^2 + \Delta z^2} \nonumber \] Para passar a soma de Rimann para integral temos que aplicar o teorema do valor médio 3 vezes em cada subintervalo $[t_{i-1}, t_i]$ e disso concluímos que
- Deve existir um número $t_l^*$ em $[t_{i-1}, t_i]$ tal que \[ \Delta x = x'\left( t_l^* \right) \Delta t_l \nonumber \]
- Deve existir um número $t_l^{**}$ em $[t_{i-1}, t_i]$ tal que \[ \Delta y = y'\left( t_l^{**} \right) \Delta t_l \nonumber \]
- Deve existir um número $t_l^{***}$ em $[t_{i-1}, t_i]$ tal que \[ \Delta z = z'\left( t_l^{***} \right) \Delta t_l \nonumber \]
| Definição |
|
Se $C$ é uma curva suave definida pela função vetorial $\mathbf{r}$ no intervalo $[a,b]$, então o comprimento (arco) de $C$ nesse intervalo está dado por \[ s = \int_a^b \left| \dfrac{d\mathbf{r}}{dt} \right|\;\; dt \] |
Observe que para se \[ \mathbf{v}(t) = \dfrac{d\mathbf{r}(t)}{dt}\;\;\;\;\;\;t\in\left[a,\,b\right] \nonumber \] então \[ \begin{align*} s =& \int_a^b \left|\mathbf{v}(t) \right|\;\; dt\\ =& \int_a^b \sqrt{v_x^2 + v_y^2 + v_z^2}\;\; dt \end{align*} \]
Exemplo 03
Encontre o comprimento arco da curva dada por $\mathbf{r}(t) = t \,\mathbf{i} + \dfrac{4}{3}t^{3/2}\,\mathbf{j} + \dfrac{1}{2}t^{2} \,\mathbf{k}$ entre $t=0$ e $t=2$.
Exemplo 04
Encontre o comprimento do arco de uma hélice depois de completar uma volta inteira, sabendo que a parametrização da curva está dada por $\mathbf{r}(t) = a\cos t \,\mathbf{i} + a \sin t \,\mathbf{j} + \sqrt{1-a^2} t \,\mathbf{k}$
Função de comprimento de arco
Em algumas situações (como no cálculo da curvatura de uma curva) é conveniente que o parâmetro da equação vetorial represente o comprimento de arco. Por exemplo, se uma equação vetorial para a curva $C$ é \[ \mathbf{r}(t) = f(t) \,\mathbf{i} + g(t) \,\mathbf{j} + h(t) \,\mathbf{k} \nonumber \] então em lugar de $t$, podemos empregar como parâmetro o número de unidades de comprimento de arco $l$ medidos desde o ponto $P_0\left( f\left(t_0\right),\,g\left(t_0\right),\, h\left(t_0\right) \right)$ de $C$, até o ponto $P_0\left( f\left(t\right),\,g\left(t\right),\, h\left(t\right) \right)$, elegido arbitrariamente. Considere que $s$ aumenta conforme $t$ cresce, de modo que $s$ é positivo se o comprimento do arco é medido na mesma direção de crescimento de $t$ e negativo se é medido na direção oposta. Por tanto, $s$ é uma distância dirigida. A cada valor de $s$ corresponde um solo ponto $P$ de $C$. Assim, as coordenadas de $P$ são funções de $s$ e $s$, seguidamente, é uma função de $T$.
| Definição de função vetorial |
|
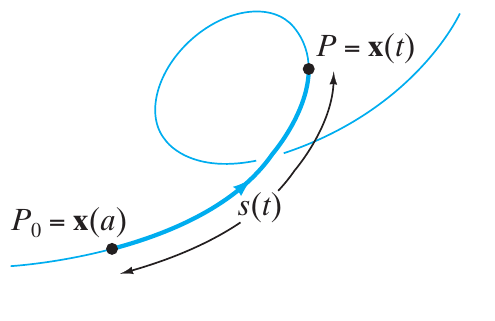
Seja $\mathbf{r}(t)$ qualquer caminho $C^1$ e assuma que a derivada é $\mathbf{r}'(t)$ nunca é zero (então suave). Fixe um ponto $P_o$ no caminho e seja $a$ tal que $\mathbf{r}(a)=P_o$. Definimos uma função $L(t)$ de uma variável que mede o comprimento do caminho entre $P_o$ e qualquer outro ponto $P$ (móvel) por \[ s(t) = \int_a^t \left| \dfrac{d\mathbf{r}}{dt} \right|\;\; dt \label{s(t)} \] |
Pelo teorema fundamental do cálculo \[ \dfrac{ds}{dt}= \left| \dfrac{d\mathbf{r}}{dt} \right| = \left| \mathbf{v} \right| \label{rel01} \] por definição o vetor tangente coincide com o vetor velocidade \[ \mathbf{T} = \mathbf{v} \nonumber \] e a partir deste definimos o vetor tangente unitário \[ \mathbf{\hat{T}} = \dfrac{\mathbf{v}}{\left| \mathbf{v} \right|} \nonumber \] Multiplicando por $\mathbf{\hat{T}}$ a relação $\ref{rel01}$ e comparando com o resultado anterior, temos \[ \mathbf{v}(t) = \dfrac{ds}{dt} \mathbf{\hat{T}} \]
Reparametrização em termos do comprimento de arco
Reparametrização
Resulta interessante traçar paralelos entre a função vetorial $\mathbf{r}(t)$ e a posição de um partícula (assim o parámetro $t$ pode ser o tempo), dado o fato de que sua derivada nos dará a velocidade com a partícula se move sobre a trajetória. Nesse sentido nos podemos entender a reparametrização da função vetorial como uma escolha de um vetor posição o qual resulta em uma nova velocidade de recorrido, como mostramos a continuação: Suponhamos que os valos de $t$ estão todos contidos no subconjunto $I=[a,\,b]\subset \mathbb{R}$ e que existe uma função $\phi:J\to I$, isto é $t=\phi(\tau)$. Reparametrizar significa construir uma nova função que resulta da composição de $\mathbf{r}(t)$ com $\phi(\tau)$, isto é \[ \mathbf{\bar{r}}(\tau) = \mathbf{r}(t) \circ \phi(\tau) = \mathbf{r}\left( \phi(\tau) \right) \nonumber \] se derivamos esta expressão obtemos \[ \mathbf{\bar{r}}'(\tau) = \mathbf{r}'\left( \phi(\tau) \right) \phi '(\tau) \nonumber \] por exemplo considere a equação vetorial $\mathbf{r}(t)=\left< t,t^2 \right>$ definida entre $[-1,1]$ e seja $\phi:[0,2\pi] \to [-1,1]$ a função definida por $t=\phi (\tau)=-\cos \tau$
Então da figura acima se observa que enquanto $\mathbf{r}(t)$ percorre a parábola uma vez, $\mathbf{r}(\tau)$ a percorre duas vezes. Outra observação importante a ser feita é que a rapidez (modulo da velocidade) com que é percorrida a curva é maior para o caso em que se parametriza com $t$ do que com $\tau$: enquanto $\mathbf{r}(t)$ leva 2 unidades de tempo em ir desde $\mathbf{r}(-1)=\left< -1,\, 1 \right>$ até $\mathbf{r}(1)=\left< 1,\, 1 \right>$, enquanto que $\mathbf{\bar{r}}(\tau)$ leva $\pi$ unidades de tempo em ir desde $\mathbf{\bar{r}}(0)=\left< -1,\, 1 \right>$ até $\mathbf{\bar{r}}(\pi)=\left< 1,\, 1 \right>$ unidades de tempo para volver desde $\mathbf{\bar{r}}(0)=\left< -1,\, 1 \right>$ até $\mathbf{\bar{r}}(\pi)=\left< 1,\, 1 \right>$ e $\pi$.
Reparametrização em termos do comprimento de arco
A ideia de se fazer esta reparametrização é obter uma parametrização tal que a velocidade com que é percorrido o trajeto da curva seja constante e igual à unidade de forma tal que o tempo dispensado em percorre a curva seja exatamente igual ao comprimento da curva, isto é, esperamos que \[ s = \int_a^b \left| \dfrac{d\mathbf{\bar{r}}(s)}{dt} \right|\;\; dt = \int_a^b 1\,dt = b - a \nonumber \]
Para obter a curva parametrizada em termos do comprimento de arco devemos seguir os seguintes passos
- Calcular a função comprimento de arco
- Encontrar a inversa da função comprimento de arco, ou seja obter $t=t(s)$, $0\leq s \leq l$
- Substituir na equação vetorial original o termos reescrito em termos o comprimento de arco.
Exemplo 05
Calcular a função comprimento de arco para a hélice $\mathbf{r}(t) = a\cos t\,\mathbf{i} + a\sin t \,\mathbf{j} + bt\,\mathbf{k}$, selecionado $P_o = a\,\mathbf{i}$
Exemplo 06
Dada uma curva $C$ representada por $\left| \mathbf{r}(t) \right|=1$, então o parâmetro $t$ é o parâmetro comprimento de arco de $C$
Exemplo 07
Calcule a curva parametrizada em termo do comprimento de arco da função vetorial $\mathbf{r}(t) = t \,\mathbf{i} + \dfrac{\sqrt{2}}{2}t^2\,\mathbf{j} + \dfrac{1}{3}t^3\,\mathbf{k}$
Funções vetoriais de varias variáveis
Em todas as situações vista ate aqui, cada umas das funções componente da função vetorial são todas definidas em $\mathbb{R}$. Mas similarmente ao que foi feito com as funções o domínio de nossas componentes pode ser $\mathbb{R}^3$, isto é \[ \mathbf{r}(x,y,z) = f(x,y,z)\,\mathbf{i} + g(x,y,z) \,\mathbf{j} + h(x,y,z) \,\mathbf{k} \nonumber \] Vejamos um exemplo \[ \mathbf{r}(x,y,z) = xz\,\mathbf{i} + xy \,\mathbf{j} + 2\sqrt{z} \,\mathbf{k} \nonumber \] outro \[ \mathbf{r}(x,y,z) = x \,\mathbf{i} + \sqrt{1-x^2-y^2} \,\mathbf{j} \nonumber \]