Área de uma superfície

Nosso objetivo desta seção é calcular a área de uma superfície suave, utilizando os conceitos estudados até aqui.

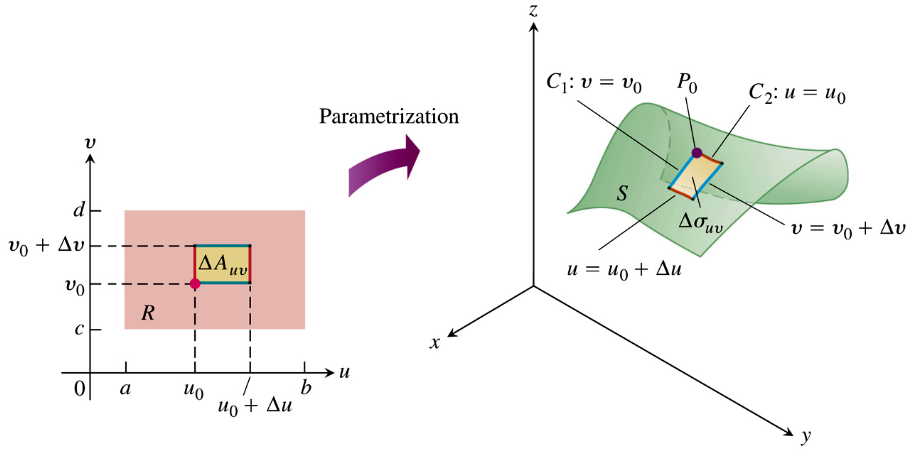
Como discutido anteriormente, quando escolhemos uma parametrização $\mathbf{r}(u,v)$ para representar uma superfície definida em $\mathbb{R}^3$ estamos na verdade mapeando pontos no espaço $\{u,v\}\in D[\mathbf{r}] \subset \mathbb{R}^2$, em pontos $\{x,y,z\} \in \mathbb{R}^3$ os quais definem a superfície $S$.

Agora, consideremos um pequeno elemento de área, $\Delta A$, definido no domínio da parametrização, $D[\mathbf{r}]$, conforme se monstra do lado direito da figura acima. Observe que as coordenadas dos pontos que definem o paralelepípedo são $\left\{ \left( u_0,\,v_0 \right),\, \left( u_0+\Delta u,\,v_0 \right),\, \left( u_0+\Delta u,\,v_0 + \Delta v\right),\, \left( u_0,\,v_0 + \Delta v \right) \right\}$. Como resultado da aplicação da parametrização sobre $\Delta A$ obteremos uma superfície $\Delta \sigma$ definida em $S$. A área $\Delta \sigma$ é delimitada por duas $u$-curvas \[ C_1:\,\mathbf{r}\left( u,\,v_0 \right)\;\;\;\;\;\;\;C_1':\,\mathbf{r}\left( u,\,v_0 +\Delta v\right), \nonumber \] e por duas $v$-curvas: \[ C_2:\,\mathbf{r}\left( u_0,\,v \right)\;\;\;\;\;\;\;C_2':\,\mathbf{r}\left( u_0+\Delta u,\,v_0\right) \nonumber \]

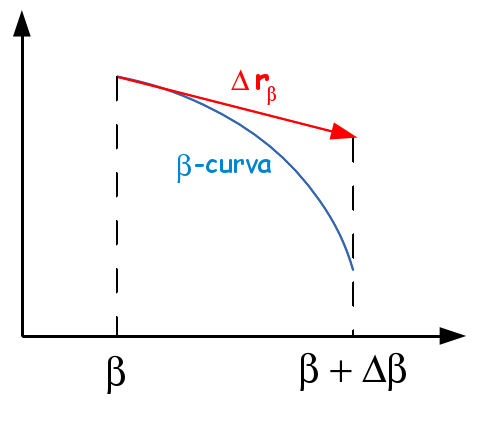
Consideremos uma $\beta$-curva (o $\beta$ pode ser $u$ ou $v$), o comprimento dessa $\beta$-curva pode ser aproximado pelo comprimento do vetor o qual por sua vez se aproxima da derivada: \[ \begin{align*} \Delta r_\beta =& \mathbf{r}\left( \beta + \Delta \beta \right) - \mathbf{r}\left( \beta \right)\\ \dfrac{\Delta r_\beta}{\Delta \beta} =& \dfrac{\left|\mathbf{r}\left( \beta + \Delta \beta \right) - \mathbf{r}\left( \beta \right)\right|}{\Delta \beta}\\ \dfrac{\Delta r_\beta}{\Delta \beta} \approx& \left|\, \dfrac{d\mathbf{r}}{d\beta} \,\right|\\ \Delta r_\beta \approx& \left|\, \dfrac{d\mathbf{r}}{d\beta} \,\right| \, \Delta \beta\\ \Delta r_\beta \approx& \left|\, \mathbf{T}_\beta \,\right| \, \Delta \beta\\ \end{align*} \] Observe que este resultado sugere que podemos definir um vetor $\Delta \mathbf{r}_\beta$ ao longo da curva $\beta$ se removemos o valor absoluto \[ \Delta \mathbf{r}_\beta \approx \, \mathbf{T}_\beta\,\Delta \beta \nonumber \]

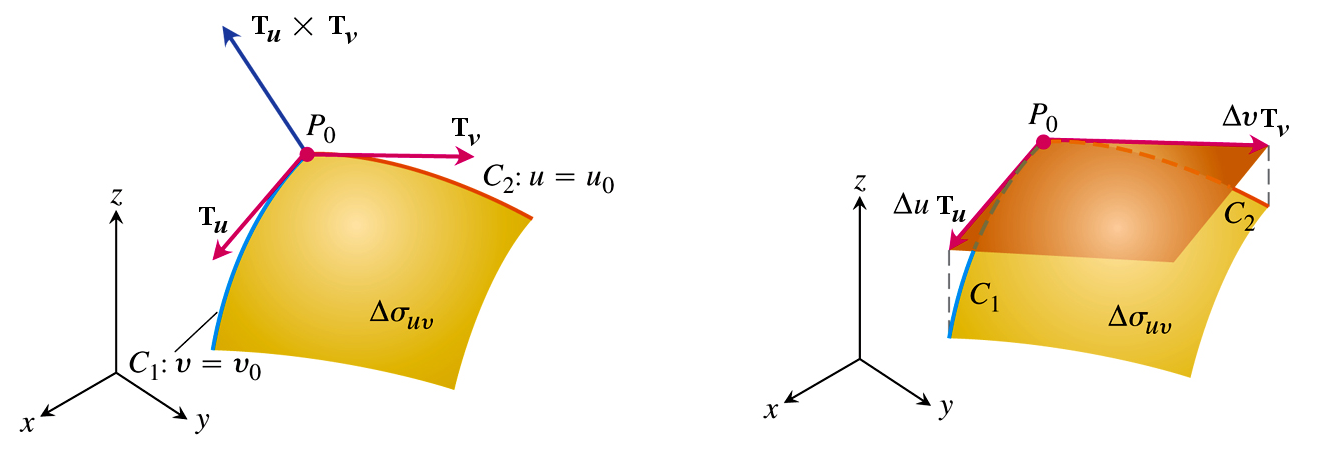
Lembrando que $\beta$ pode ser $u$ ou $v$, termos expressões similares a essa para $u$ ou $v$ \[ \Delta \mathbf{r}_u \approx \, \mathbf{T}_u\,\Delta u\;\;\;\;\;\;\;\;\;\Delta \mathbf{r}_v \approx \, \mathbf{T}_v\,\Delta v \nonumber \]

Da figura acima vemos que a área do elemento de área $\Delta \sigma$ se aproxima da área do paralelepípedo formado pelos vetores $\Delta \mathbf{r}_u$ e $\Delta \mathbf{r}_v$

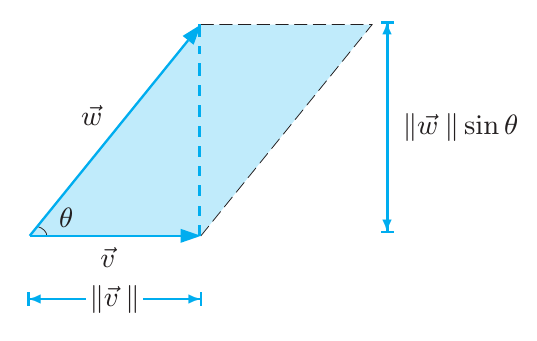
A área do paralelepípedo está dada pelo dobro da área dos dois triângulos formados, isso é \[ \begin{align*} \Delta \sigma \approx& \text{base}\,\cdot\, \text{altura}\\ \approx& \left|\, \mathbf{T}_u \,\right|\,\Delta u\, \left|\, \mathbf{T}_v \,\right|\,\Delta v \sin \theta\\ \approx& \left|\, \mathbf{T}_u \times \mathbf{T}_v \,\right|\,\Delta u\,\Delta v \end{align*} \] Assim, a área de toda a superfície será a soma de todas as pequenas áreas, no limite em que $\Delta u \to 0$ e $\Delta v \to 0$, \[ A = \lim_{\begin{align*} \Delta u \to& 0\\ \Delta v \to& 0 \end{align*}} \sum_i \Delta \sigma_i \] que é por definição (a soma de Riemman) a integral dupla:

Integral de superfície de uma função definida vetorialmente

A área de uma superfície suave está dada por \[ A_S = \iint_D d\sigma \nonumber \] onde \[ d\sigma = \left|\, \mathbf{n} \,\right|\, du\,dv = \left|\, \mathbf{T}_u \times \mathbf{T}_v \,\right|\, du\,dv \nonumber \]

Relação com a matriz Jacobiana

Suponha que nossa superfície é parametrizada da seguinte forma \[ \begin{align*} x =& x(u,v)\\ y =& y(u,v)\\ z =& z(u,v)\\ \end{align*} \] consequentemente \[ \begin{align*} \mathbf{T}_u =& \frac{\partial x}{\partial u}\,\mathbf{i} + \frac{\partial y}{\partial u} \,\mathbf{j} + \frac{\partial z}{\partial u} \,\mathbf{k}\\ \mathbf{T}_v =& \frac{\partial x}{\partial v}\,\mathbf{i} + \frac{\partial y}{\partial v} \,\mathbf{j} + \frac{\partial z}{\partial v} \,\mathbf{k} \end{align*} \] de forma que \[ \begin{align*} \mathbf{n} =& \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & \frac{\partial z}{\partial u}\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & \frac{\partial z}{\partial v} \end{vmatrix}\\ =& \left(\, \frac{\partial y}{\partial u}\, \frac{\partial z}{\partial v} - \frac{\partial y}{\partial v}\, \frac{\partial z}{\partial u}\, \right)\, \mathbf{i} - \left(\, \frac{\partial x}{\partial u}\, \frac{\partial z}{\partial v} - \frac{\partial x}{\partial v}\, \frac{\partial z}{\partial u} \, \right)\,\mathbf{j} + \left(\, \frac{\partial x}{\partial u}\, \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v}\, \frac{\partial y}{\partial u} \, \right)\,\mathbf{k}\\ =& \left(\, \frac{\partial y}{\partial u}\, \frac{\partial z}{\partial v} - \frac{\partial y}{\partial v}\, \frac{\partial z}{\partial u}\, \right)\, \mathbf{i} + \left(\, \frac{\partial z}{\partial u}\,\frac{\partial x}{\partial v} - \frac{\partial z}{\partial v}\,\frac{\partial x}{\partial u} \, \right)\,\mathbf{j} + \left(\, \frac{\partial x}{\partial u}\, \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v}\, \frac{\partial y}{\partial u} \, \right)\,\mathbf{k}\\ \end{align*} \] A continuação introduzimos o determinante Jacobiano como \[ \frac{\partial \left(\, x,y\,\right)}{\partial \left(\, u,v\,\right)} = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}\\ \end{vmatrix}= \frac{\partial x}{\partial u}\, \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v}\, \frac{\partial y}{\partial u} \nonumber \] utilizando essa expressão para escrever o vetor normal, teremos \[ \mathbf{n} = \frac{\partial \left(\, y,z\,\right)}{\partial \left(\, u,v\,\right)}\,\mathbf{i} + \frac{\partial \left(\, z,x\,\right)}{\partial \left(\, u,v\,\right)}\,\mathbf{j} + \frac{\partial \left(\, x,y \,\right)}{\partial \left(\, u,v\,\right)}\,\mathbf{k} \nonumber \] Com esta nova notação reescrevemos o diferencial de área como

\[ d \sigma = \sqrt{\left( \, \frac{\partial \left(\, y,z\,\right)}{\partial \left(\, u,v\,\right)} \, \right)^2 + \left( \, \frac{\partial \left(\, z,x\,\right)}{\partial \left(\, u,v\,\right)} \, \right)^2 + \left( \, \frac{\partial \left(\, x,y \,\right)}{\partial \left(\, u,v\,\right)} \, \right)^2\;\,\,}\,\,\,du\,dv \nonumber \]

Superfícies definidas de forma explicita

Se a superfície está definida de forma explicita, isto é \[ z=z(x,y) \nonumber \] então temos que uma parametrização para essa superfície é \[ \mathbf{r}(x,y) = x\,\mathbf{i} +y \,\mathbf{j} + z(x,y) \,\mathbf{k} \nonumber \] disso \[ \begin{align*} \mathbf{T}_x =& \dfrac{\partial \mathbf{r}}{\partial x}\\ =& \,\mathbf{i} + \dfrac{\partial z}{\partial x}\mathbf{k}\\ \mathbf{T}_y =& \dfrac{\partial \mathbf{r}}{\partial y}\\ =& \,\mathbf{j} + \dfrac{\partial z}{\partial y}\mathbf{k}\\ \mathbf{n} =& \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ 1 & 0 & \dfrac{\partial z}{\partial x}\\ 0 & 1 & \dfrac{\partial z}{\partial y} \end{vmatrix}\\ =& -\dfrac{\partial z}{\partial x}\,\mathbf{i} - \dfrac{\partial z}{\partial y} \,\mathbf{j} + \mathbf{k}\\ \left|\, \mathbf{n} \,\right| =& \sqrt{1 + \left( \dfrac{\partial z}{\partial x} \right)^2 + \left(\dfrac{\partial z}{\partial y} \right)^2\;} \end{align*} \] o que no leva a expressar

Integral de superfície de uma função definida explicitamente

A integral de uma função definida explicitamente, isto é $z=z(x,y)$ se obtém a partir de \[ A_S = \iint_D d\sigma \nonumber \] onde \[ d\sigma = \sqrt{1 + \left( \dfrac{\partial z}{\partial x} \right)^2 + \left(\dfrac{\partial z}{\partial y} \right)^2\;}\, dx\,dy \nonumber \] Similarmente, quando a superfícies é definidas como $y=y(x,z)$ teremos \[ d\sigma = \sqrt{1 + \left( \dfrac{\partial y}{\partial x} \right)^2 + \left(\dfrac{\partial y}{\partial z} \right)^2\;}\, dx\,dz \nonumber \] e quando $x=x(y,z)$, \[ d\sigma = \sqrt{1 + \left( \dfrac{\partial x}{\partial y} \right)^2 + \left(\dfrac{\partial x}{\partial z} \right)^2\;}\, dy\,dz \nonumber \]

Área das superfícies definidas de forma implícita

Para o caso em que a superfície é definida como \[ F(x,y,z)=c \nonumber \] O teorema da função explicita (tema de calculo avanzado) garante que $F(x,y,z)=c$ é o gráfico de uma função diferenciável $z=z(x,y)$, mesmo que não se conheça dita função, se isso é verdade então uma representação vetorial dessa superfície seria \[ \mathbf{r}(x,y) = x\,\mathbf{i} +y \,\mathbf{j} + z(x,y) \,\mathbf{k} \nonumber \] de onde \[ \begin{align*} \mathbf{T}_x =& \dfrac{\partial \mathbf{r}}{\partial x}\\ =& \,\mathbf{i} + \dfrac{\partial z}{\partial x}\mathbf{k}\\ \mathbf{T}_y =& \dfrac{\partial \mathbf{r}}{\partial y}\\ =& \,\mathbf{j} + \dfrac{\partial z}{\partial y}\mathbf{k} \end{align*} \] Antes de continuar, note que a função definida de forma explicita pode ser escrita como \[ F\left( x,\, y,\, z(x,y)\right)=0 \nonumber \] derivando em relação a $x$ e logo a $y$, e utilizando a regra da cadeia \[ \begin{array}{ccrc} \dfrac{\partial F}{\partial x} &=& \dfrac{\partial F}{\partial x}\cancelto{1}{\dfrac{\partial x}{\partial x}} + \dfrac{\partial F}{\partial y}\cancelto{0}{\dfrac{\partial y}{\partial x}} + \dfrac{\partial F}{\partial z}\dfrac{\partial z}{\partial x} &=& 0\\ & & \dfrac{\partial F}{\partial x} + \dfrac{\partial F}{\partial z}\dfrac{\partial z}{\partial x} &=& 0\\ & & \dfrac{\partial z}{\partial x} &=& -\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}\\ & & \dfrac{\partial z}{\partial x} &=& -\dfrac{F_x}{F_z}\\ \dfrac{\partial F}{\partial y} &=& \dfrac{\partial F}{\partial x}\dfrac{\partial x}{\partial y} + \dfrac{\partial F}{\partial y}\dfrac{\partial y}{\partial y} + \dfrac{\partial F}{\partial z}\dfrac{\partial z}{\partial y} &=& 0\\ & & \dfrac{\partial F}{\partial y} + \dfrac{\partial F}{\partial z}\dfrac{\partial z}{\partial y} &=& 0\\ & & \dfrac{\partial z}{\partial y} &=& -\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}\\ & & \dfrac{\partial z}{\partial y} &=& -\dfrac{F_y}{F_z}\\ \end{array} \nonumber \] dessa forma \[ \begin{align*} \mathbf{T}_x =& \,\mathbf{i} - \dfrac{F_x}{F_z}\mathbf{k}\\ \mathbf{T}_y =& \,\mathbf{j} - \dfrac{F_y}{F_z}\mathbf{k} \end{align*} \] e \[ \begin{align*} \mathbf{n} =& \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ 1 & 0 & - \dfrac{F_x}{F_z}\\ 0 & 1 & - \dfrac{F_y}{F_z} \end{vmatrix}\\ =& \dfrac{F_x}{F_z}\,\mathbf{i} + \dfrac{F_y}{F_z} \,\mathbf{j} + \mathbf{k}\\ =& \dfrac{F_x\,\mathbf{i} + F_y\,\mathbf{j} + F_z\,\mathbf{k}}{F_z}\\ \left|\, \mathbf{n} \,\right| =& \dfrac{\sqrt{F_x^2+F_y^2 + F_z^2}}{F_z} \end{align*} \] Como \[ \vec{\nabla}\,F = \dfrac{\partial F}{\partial x}\,\mathbf{i} + \dfrac{\partial F}{\partial y} \,\mathbf{j} +\dfrac{\partial F}{\partial z} \,\mathbf{k} = F_x\,\mathbf{i} +F_y \,\mathbf{j} + F_z \,\mathbf{k} \nonumber \] e \[ \vec{\nabla}\,F\,\cdot\,\mathbf{k} = \dfrac{\partial F}{\partial z} = F_z \nonumber \] de forma que \[ \left|\, \mathbf{n} \,\right| = \dfrac{\left|\, \vec{\nabla}F \,\right|}{\left|\, \vec{\nabla}F\cdot \mathbf{k}\,\right|} \nonumber \] Observe que no denominador temos o produto escalar do gradiente da função com $\mathbf{k}$, no entanto, se for feito outra escolha na forma implícita, teríamos resultados diferentes \[ \begin{align*} \text{Se }F\left( x,\, y(x,z),\, z\right)=0 \Rightarrow & \left|\, \mathbf{n} \,\right| = \dfrac{\left|\, \vec{\nabla}F \,\right|}{\vec{\nabla}F\cdot \mathbf{j}}\\ \text{Se }F\left(x(y,z),\, x,\, z\right)=0 \Rightarrow & \left|\, \mathbf{n} \,\right| = \dfrac{\left|\, \vec{\nabla}F \,\right|}{\vec{\nabla}F\cdot \mathbf{i}}\\ \end{align*} \] Podemos expressar estes resultados da seguinte forma genérica,

Integral de superfície de uma função implícita

Seja a superfície $S$ definida de forma explicita pela função $F(x,y,z)=c$ e seja $R$ a projeção dessa superfície em algum plano o qual é caraterizado pelo vetor normal $\,\mathbf{p}$, a área da superfície $S$ está dada por \[ A_S = \iint_D d\sigma \nonumber \] onde \[ d\sigma = \dfrac{\left|\, \vec{\nabla}F \,\right|}{\left|\, \vec{\nabla}F\cdot \mathbf{p}\,\right|}\,da \nonumber \] onde $da$ é o elemento de área no plano $R$

Observe que está forma de expressar o diferencial de área pode ser utilizada para integral mesmo para o caso em que a superfície está expressada de forma explicita.

Integrais em coordenas polares

Quando integradas superfícies que são expressadas de forma implícita ou explicita muitas vezes resulta adequado transformar a integral para coordenadas polares

A transformação de variáveis necessárias para realizar essa mudança de base é a seguinte \[ r^2=x^2+y^2\;\;\;\;\;\;x=r\cos\,\theta\;\;\;\;\;\;y=r\sin\,\theta \nonumber \] dessa forma, a integral passa a ser escrita como \[ \iint_R f(x,y)da = \int_\alpha^\beta\int_a^b f\left( r\cos\,\theta,\, r\sin\,\theta\right)\,r\,dr\,d\theta \nonumber \]

Exemplo 01

Seja o paraboloide $\displaystyle z=2\left( x^2 + y^2 \right)$, abaixo de $z=8$, calcule sua área.

Exemplo 02

Seja $S$ definida por $\displaystyle z=\sqrt{a^2-x^2-y^2}$ (semi esfera superior), calcule sua área.

Exemplo 03

Dado enunciado do exemplo 01, considere a função de forma definida explicitamente e calcule sua superfície

Exemplo 04

Encontre a área da esfera $x^2+y^2+z^2=2$ que está delimitada pelo cone $z=\sqrt{x^2+y^2}$

Exemplo 04

Seja $S$ a superfície de uma bola de futbol americano formada ao gira a curva $x=\cos\,z$, $y=0$, $\pi/2\leq z \leq \pi/2$ ao redor do eixo $z$. Encontre uma parametrização e calcule a área da superfície.

Exemplo 05

Se a parametrização de um helicoide está dada por \[ x = u\cos\,v\;\;\;\;\;\;y=u\sin\,v\;\;\;\;\;\;z=v \nonumber \] onde $0 \leq u\leq 1$ e $0\leq v \leq 2\pi$, calcule a área da sua superfície.

Exemplo 06

Encontrar a área de um toro o qual é parametrizada pela equação \[ \mathbf{r}(u,v) = \left( 2+\cos u \right) \cos v+ \,\mathbf{i} + \left( 2+\cos u \right) \sin v\,\mathbf{j} +\sin u \,\mathbf{k} \nonumber \] onde $0\leq u \leq 2\pi$ e $0\leq v \leq 2\pi$.

Exemplo 06

Calcule a área da cúpula obtida a partir da interseção da esfera $x^2+y^2+z^2=2$ e o cilindro $x^2+y^2=1$.

Exemplos