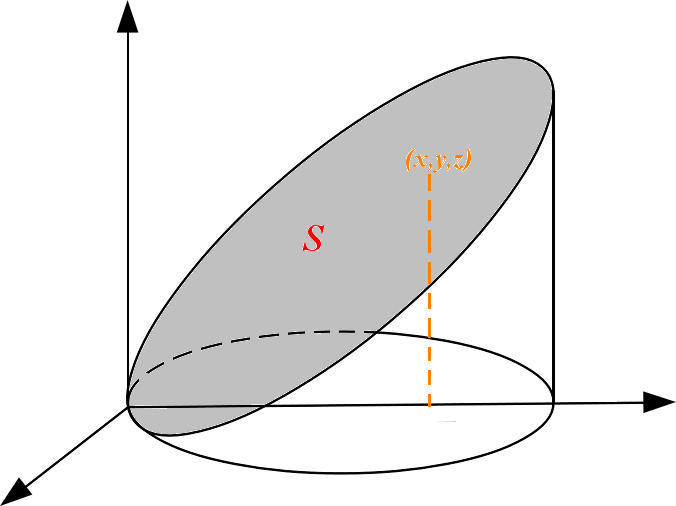
Integral de Superfície de um campo escalar

Suponhamos que desejamos calcular a massa de uma superfície, para isso será necessário conhecer o valor da densidade de massa por unidade de área , $G(x,y,z)$, e multiplicar essa densidade de massa por cada elemento diferencial de área, $\Delta \sigma$, algo como \[ \Delta \left(m_S\right)_i = G(x_i,y_i,z_i)\, \Delta \sigma_i \nonumber \] Somando todos os elementos de massa teremos que a massa total estará dada por \[ m_S = \lim_{n\to \infty} \sum_{i=1}^{n}f(x_i,y_i,z_i)\, \Delta \sigma_i = \iint_D G(x,y,z)\,d\sigma \nonumber \] onde nessa expressão entendemos que \[ \Delta \sigma_i \approx \left|\, \mathbf{T}_u \times \mathbf{T}_v \,\right|\,\Delta u\,\Delta v \nonumber \] e por tanto dizer que $n\to \infty \Rightarrow \Delta\,\sigma \to 0$ o qual se traduz para $\Delta u\to 0$ e $\Delta v\to 0$. Dessa forma podemos expressar esse resultado na seguinte definição a qual é valida para qualquer campo escalar (no lugar da massa poderiamos ter a densidade de carga ou querer calcular o centro de massa, etc)

Definição

Seja $G(x,y,z)$ uma função continua definida sobre uma superfície suave $S$, se $S$ é definida de forma vetorial como \[ \mathbf{r}(u,v) = f(u,v)\,\mathbf{i} + h(u,v) \,\mathbf{j} + g(u,v) \,\mathbf{k} \nonumber \] a integral de superfície de $G$ sobre $S$ se define como \[ \iint_D G(x,y,z)\,d\sigma = \iint_D G(x,y,z)\left|\, \mathbf{T}_u \times \mathbf{T}_v \,\right|\,du\,dv \nonumber \] se $S$ é definida de forma explicita, isto é \[ z = F(x,y) \nonumber \] a integral de superfície de $G$ sobre $S$ se define como \[ \iint_D G(x,y,z)\,d\sigma = \iint_R G(x,y,z)\, \sqrt{\left( \dfrac{\partial F}{\partial x} \right)^2 + \left( \dfrac{\partial F}{\partial y} \right)^2 + 1\,\,\,}\,\,dx\,dy \nonumber \] onde $R$ é a superfície projetada no plano $xy$ se $S$ é definida de forma implícita, mediante a equação \[ F(x,y,z) = c \nonumber \] a integral de superfície de $G$ sobre $S$ se define como \[ \iint_D G(x,y,z)\,d\sigma = \iint_R G(x,y,z) \dfrac{\left|\, \vec{\nabla}F \,\right|}{\left|\, \vec{\nabla}F\cdot \mathbf{p} \,\right|}\,da \nonumber \] onde $R$ é a superfície projetada no plano que possui norma $\mathbf{p}$

Aplicações

1. Massa $m$ de uma lamina \[ m = \iint\,\delta\,d\sigma \nonumber \] onde $\delta$ é a densidade de massa por unidade de área.
2. Centro de massas \[ \begin{align*} \bar{x} =& \dfrac{1}{m}\iint\,x\,\delta\,d\sigma\\ \bar{y} =& \dfrac{1}{m}\iint\,y\,\delta\,d\sigma\\ \bar{z} =& \dfrac{1}{m}\iint\,z\,\delta\,d\sigma\\ \end{align*} \nonumber \]
3. Momento de inercia \[ I_L = \iint\,\rho^2\,\delta\,d\sigma \nonumber \] onde $\rho$ é a distância desde o ponto $P$ até o eixo $L$, por exemplo se o eixo é $z\Rightarrow \rho^2=x^2+y^2$

Exemplo 01

Calcular $\displaystyle \iint \left(z-x^2+xy^2-1\right)\,d\sigma$, onde a superfície está definida por \[ \mathbf{r}(u,v) = u \,\mathbf{i} + v \,\mathbf{j} (u^2+1) \,\mathbf{k} \nonumber \]

Exemplo 02

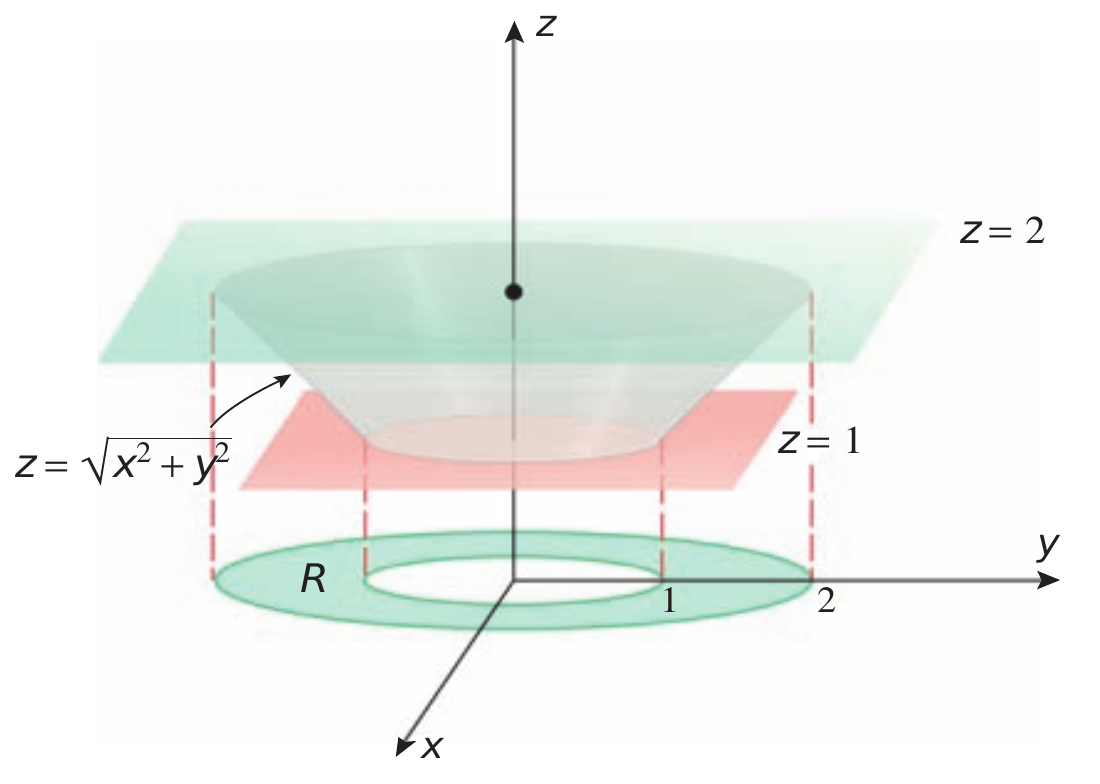
Calcular $\displaystyle \iint y^2z^2\,d\sigma$, onde $S$ é a porção cone $\displaystyle z = \sqrt{x^2+y^2}$ que está entre os planos $z=1$ e $z=2$

Exemplo 03

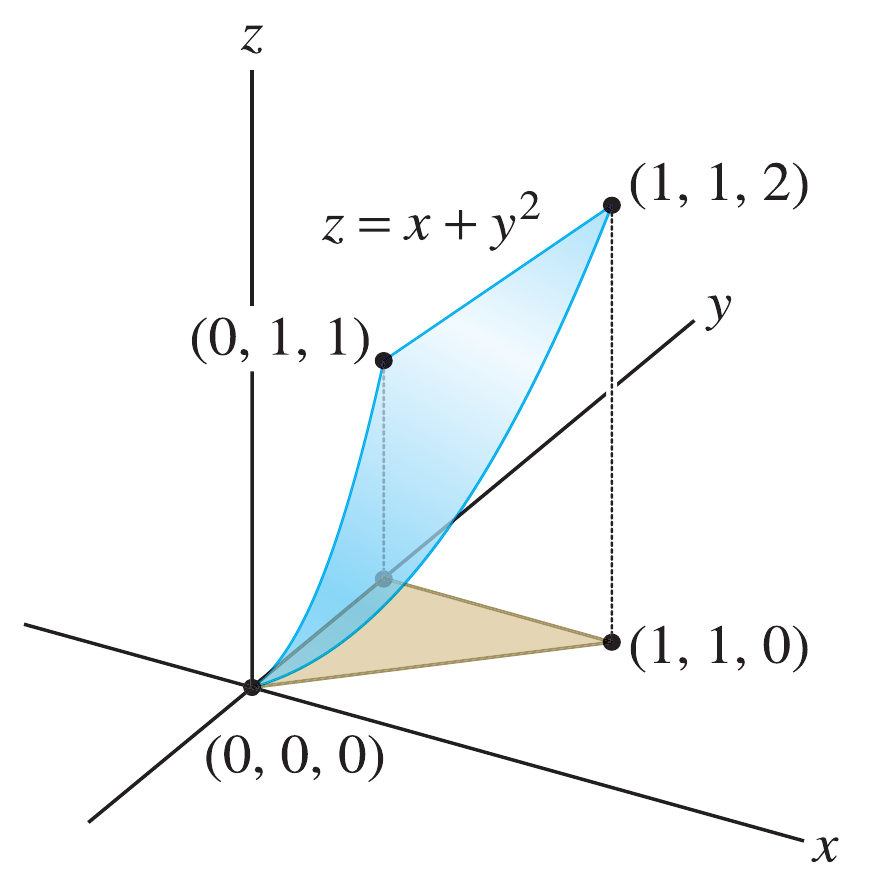
Avalie a integral $\iint \left( z-x \right) \,d\sigma$, onde $S$ é a porção do gráfico $z=x^2+y^2$, onde $0\leq x \leq y$, $0\leq y \leq 1$.

Exemplo 04

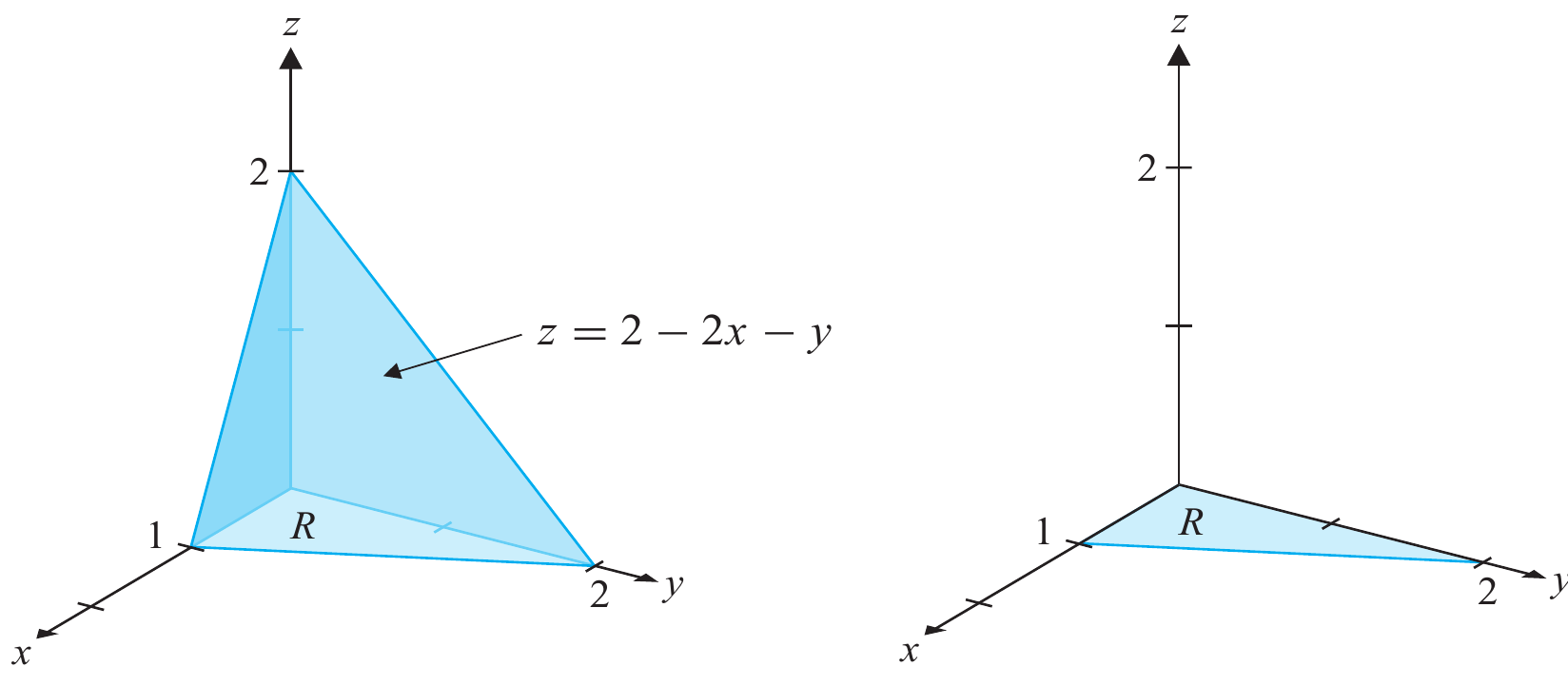
Calcular $\displaystyle \iint 3z \,d\sigma$, onde $S$ é a porção do plano $2z+y+z=2$ localizada no primeiro otante.

Exemplo 05

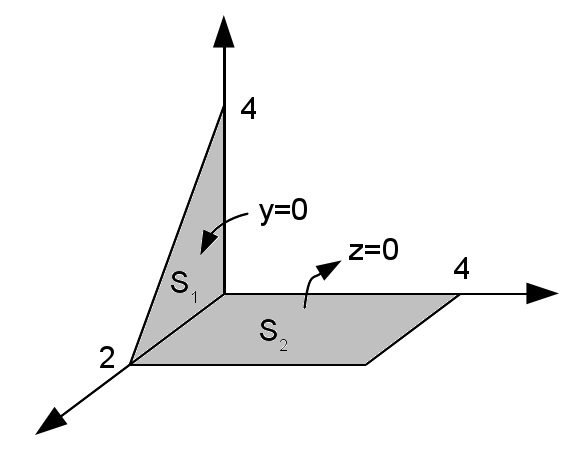
Calcular $\displaystyle \iint \left( x+y+z \right) \,d\sigma$, onde $S=S_1\cup S_2$ é a superfície

Exemplo 06

Uma lâmina ter a forma de parte do plano $z=y$ recordada pelo cilindro $x^2+\left( y-1 \right) ^2=1$. Determinar a massa dessa lâmina, se a densidade de massa é proporcional à distancia desse ponto ao plano $xy$

Exemplos