Exemplo 01
Calcular $\displaystyle \iint \left(z-x^2+xy^2-1\right)\,d\sigma$, onde a superfície está definida por
\[
\mathbf{r}(u,v) = u \,\mathbf{i} + v \,\mathbf{j} (u^2+1) \,\mathbf{k}
\nonumber
\]
para $0\leq u \leq 2$ e $0\le v \leq 5$
SOL.
\[
\begin{align*}
\mathbf{T}_u =& \,\mathbf{i} + 2u \,\mathbf{k}\\
\mathbf{T}_v =& \,\mathbf{j}
\end{align*}
\]
disso
\[
\begin{align*}
\mathbf{n} =& \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k}\\
1 & 0 & 2u\\
0 & 1 & 0
\end{vmatrix}\\
=& -2u \, \mathbf{i} + \mathbf{k }\\
\left| \, \mathbf{n} \, \right|=& \sqrt{4u^2+1}
\end{align*}
\]
de onde
\[
\begin{align*}
I =& \iint \left[\left( u^2+1 \right)-u^2+uv^2-1\right]\sqrt{4u^2+1}\,du\,dv\\
=& \int_0^5\int_0^2 \left( u^2+1-u^2+uv^2-1 \right)\sqrt{4u^2+1}\,du\,dv\\
=& \int_0^5\int_0^2 uv^2\sqrt{4u^2+1}\,du\,dv\\
\end{align*}
\nonumber
\]
seja $w=4u^2+1\Rightarrow dw=8u\,du$, e $u=0\Rightarrow w=1$, $u=2\Rightarrow w=17,$ assim
\[
\begin{align*}
I =&\int_0^5 v \,\int_1^{17} \dfrac{\sqrt{w}}{8}\,dw\,dv\\
=& \int_0^5 v\,\dfrac{\sqrt{1}}{8}\, \left[ \dfrac{2}{3} u^{3/2} \right]_1^{17}\,dv\\
=& \int_0^5 v\, \dfrac{17\sqrt{17}-1}{12}\,dv\\
=& \dfrac{17\sqrt{17}-1}{12}\,\left[ \dfrac{v^2}{2} \right]_0^5\\
=& \dfrac{125(17\sqrt{17}-1)}{24}
\end{align*}
\nonumber
\]
Exemplo 02
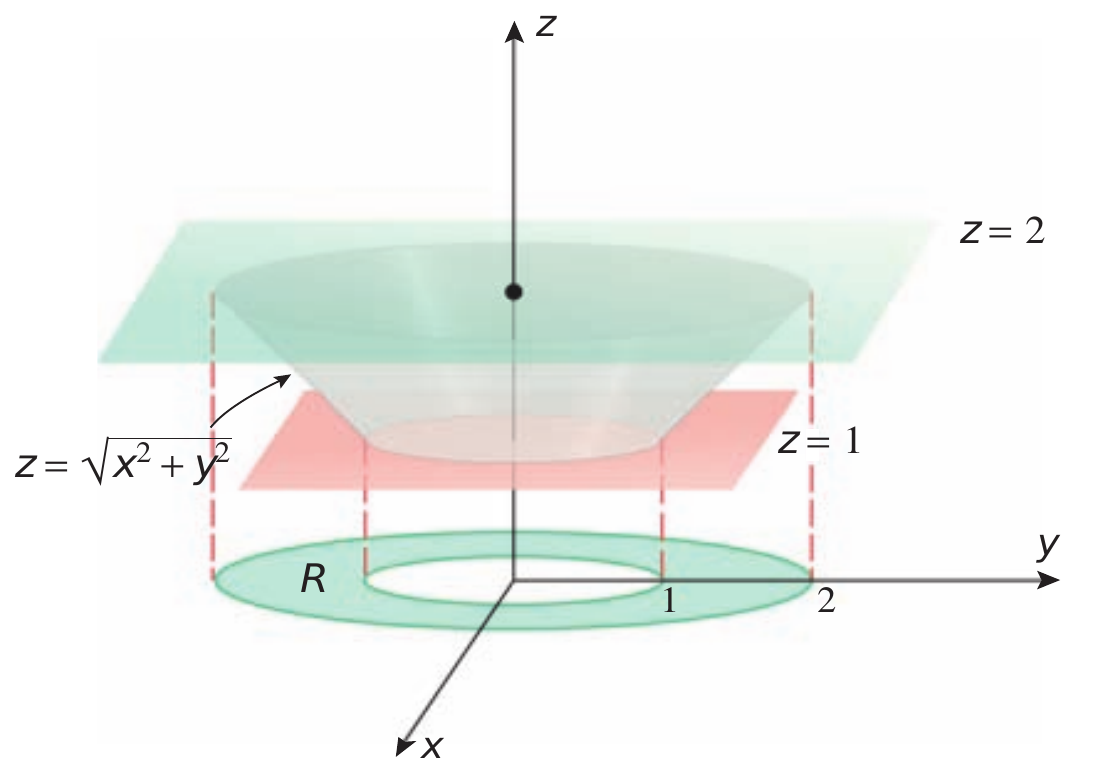
Calcular $\displaystyle \iint y^2z^2\,d\sigma$, onde $S$ é a porção cone $\displaystyle z = \sqrt{x^2+y^2}$ que está entre os planos $z=1$ e $z=2$
)
SOL.
Como a superfície está definida de forma explicita \[ \begin{align*} d\sigma =& \sqrt{\left( \dfrac{\partial F}{\partial x} \right)^2 + \left( \dfrac{\partial F}{\partial y} \right)^2 + 1\,\,\,}\,\,dx\,dy\\ =&\sqrt{\dfrac{x^2}{x^2+y^2} + \dfrac{y^2}{x^2+y^2} + 1\,\,\,}\,\,dx\,dy\\ =&\sqrt{2}\,\,dx\,dy\\ I =&\iint_{1\leq x^2+y^2\leq 4} y^2z^2\,\sqrt{2}\,\,dx\,dy\\ =&\iint_{1\leq x^2+y^2\leq 4}\sqrt{2}\, y^2 \left( x^2+y^2 \right) \,\,dx\,dy\\ \end{align*} \] passando para coordenadas polares \[ \begin{align*} I =& \sqrt{2}\int_0^{2\pi} \int_1^2 \, \left( r\,\sin\,\theta \right)^2\left( r^2 \right)\,r\,dr\,d\theta\\ =& \sqrt{2}\int_0^{2\pi} \int_1^2 r^5\,\sin^2 \theta\,dr\,d\theta\\ =& \dfrac{\sqrt{2}}{6} \int_0^{2\pi} \sin^2\theta \left[ \, r^6 \,\right]_1^2 \,d\theta\\ =& \dfrac{63\sqrt{2}}{6}\int_0^{2\pi} \sin^2\theta \,d\theta\\ \int \sin^2\theta \,d\theta =& \int \dfrac{1-\cos\,2\theta }{2}\,d\theta\\ =&\dfrac{\theta}{2} - \dfrac{\sin\,2\theta}{4}\\ I=& \dfrac{63\sqrt{2}}{6} \left[ \, \dfrac{\theta}{2} - \dfrac{\sin\,2\theta}{4} \, \right]_0^{2\pi}\\ =& \dfrac{63\sqrt{2} \,\pi}{6} \end{align*} \]
Exemplo 03
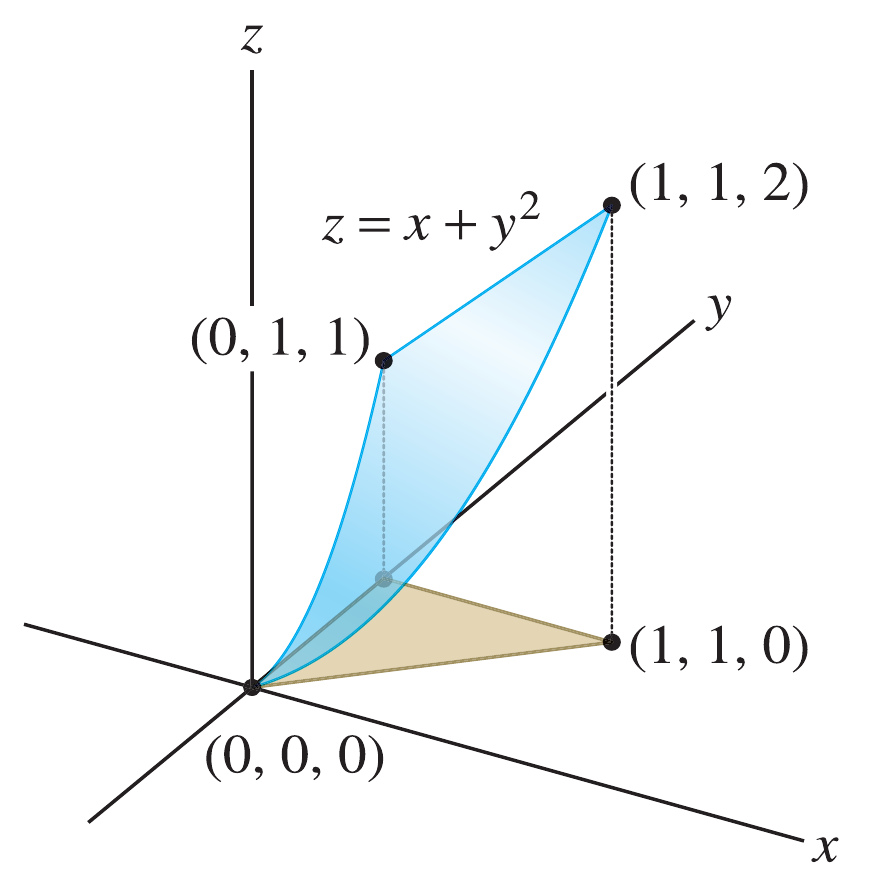
Avalie a integral $\iint \left( z-x \right) \,d\sigma$, onde $S$ é a porção do gráfico $z=x+y^2$, onde $0\leq x \leq y$, $0\leq y \leq 1$.
)
SOL.
Escrevendo de forma implícita a equação para a superfície \[ \begin{align*} \vec{\nabla}F =& \mathbf{i} + 2y \,\mathbf{j} - \,\mathbf{k}\\ \left| \, \vec{\nabla}F \, \right|=& \sqrt{1+4y^2+1}\\ \left|\vec{\nabla}F\cdot \mathbf{k} \, \right| =& 1\\ d\sigma =& \sqrt{2+4y^2}\\ I =& \iint \left( z-x \right)\sqrt{2+4y^2\,\,}\,dx\,dy\\ I =& \iint \left( x+y^2-x \right)\sqrt{2+4y^2\,\,}\,dx\,dy\\ I =& \iint y^2\sqrt{2+4y^2\,\,}\,dx\,dy \end{align*} \] Note que no plano temos que a área está delimitada pelos eixos coordenados e a reta $y=x$, de forma que nossos limites de integração serão, para $y$ desde $0$ até $1$ e para $x$, desde $0$ até $y$, assim \[ \begin{align*} I =& \int_0^x \int_0^1 y^2\sqrt{2+4y^2\,\,}\,dx\,dy\\ =& \int_0^x y^3\sqrt{2+4y^2\,\,}\,dy \end{align*} \] Aplicamos a substituição $w=2+4y^2 \Rightarrow dw = 8y\,dy$, de onde $y=0 \Rightarrow w=2$, $y=x \Rightarrow w=2+4x$ e $y^2=\dfrac{w-2}{4}$ \[ \begin{align*} I =& \int_2^6 y^2\,w^{1/2}\,\dfrac{dw}{8y}\\ =& \int_2^6 \dfrac{w-2}{4} \,w^{1/2}\,\dfrac{dw}{8}\\ =& \int_2^6 \dfrac{w^{3/2}-2w^{1/2}}{32} \,dw\\ =& \dfrac{1}{32} \left. \left( \dfrac{2}{5}u^{5/2} - \dfrac{4}{3} u^{3/2}\right) \right|_2^6\\ =& \dfrac{1}{30} \left( 6\sqrt{6} + \sqrt{2} \right) \end{align*} \]
Exemplo 04
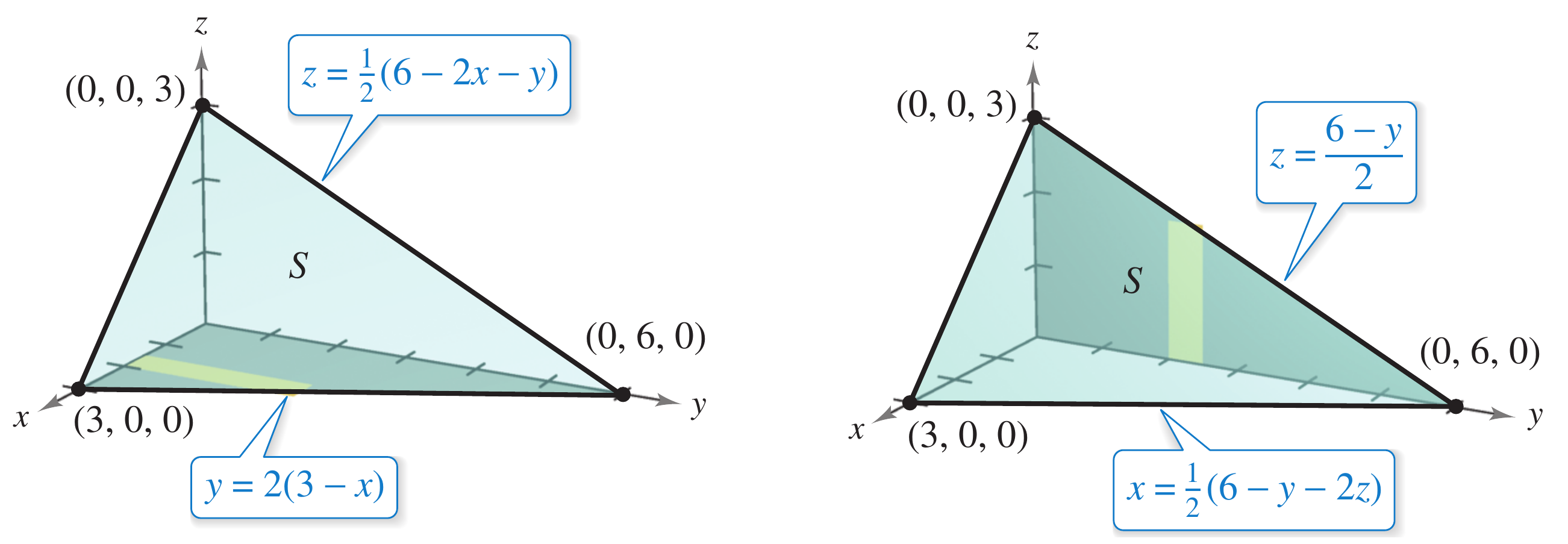
Calcular $\displaystyle \iint \left( y^2+2yz \right) \,d\sigma$, onde $S$ é a porção do plano $2x+y+2z=6$ localizada no primeiro otante.
)
SOL.
Como a equação está escrita de forma explícita \[ \begin{align*} \vec{\nabla}F =& 2\mathbf{i} + \,\mathbf{j} +2 \,\mathbf{k}\\ \left| \, \vec{\nabla}F \, \right|=& \sqrt{9}\\ =& 3\\ \left|\vec{\nabla}F\cdot \mathbf{k} \, \right| =& 2\\ d\sigma =& \dfrac{3}{2}\\ I =& \dfrac{3}{2}\iint \left( y^2+2yz \right)\,dx\,dy\\ =& \dfrac{3}{2}\iint \left( y^2+2y\left( 3-x-\dfrac{y}{2} \right) \right)\,dx\,dy\\ =& \dfrac{3}{2}\iint \left( y^2+6y-2xy-y^2 \right)\,dx\,dy\\ =& 3\iint y\left( 3-x \right) \,dx\,dy \end{align*} \] Ao projetar no plano $xy$ temos que os limites são $x=0\to 3$, $y=0\to 3\left( 3-x \right)$, assim \[ \begin{align*} I =& 3\int_0^3\int_0^{3\left( 3-x \right)} y\left( 3-x \right) \,dy\,dx\\ =& 6\int_0^3 \left( 3-x \right)^3 \,dx\\ =& -\dfrac{3}{2} \left[\left( 3-x \right)^4 \right]_0^3\\ =& \dfrac{243}{2} \end{align*} \]
SOL 2.
Vamos projetar no plano $yz$ \[ \begin{align*} \vec{\nabla}F =& 2\mathbf{i} + \,\mathbf{j} +2 \,\mathbf{k}\\ \left| \, \vec{\nabla}F \, \right|=& \sqrt{9}\\ =& 3\\ \left|\vec{\nabla}F\cdot \mathbf{x} \, \right| =& 2\\ d\sigma =& \dfrac{3}{2}\\ I =& \dfrac{3}{2}\iint \left( y^2+2yz \right)\,dy\,dz\\ =& \dfrac{3}{2}\iint \left( y^2+2yz \right)\,dy\,dz \end{align*} \] Ao projetar no plano $yz$ temos que os limites são $y=0\to 6$, $z=0\to \dfrac{1}{2}\left( 6-y \right)$, assim \[ \begin{align*} I =& \dfrac{3}{2}\int_0^6\int_0^{\left( 6-y \right)/2} \left( y^2+2yz \right)\,dz\,dy\\ =& \dfrac{3}{2} \int_0^6 \left( y^2\, \Big[ z \Big]_0^{\left( 6-y \right)/2} + 2y\,\left[\dfrac{z^2}{2} \right]_0^{\left( 6-y \right)/2} \right)\\ =& \dfrac{3}{2} \int_0^6 \left( y^2 \left( \dfrac{6-y}{2} \right) + y\,\left[\dfrac{36 - 12y + y^2}{4} \right] \right)\\ =& \dfrac{3}{8} \int_0^6 \left( 36 - y^3 \right)\\ =& \dfrac{243}{2} \end{align*} \]
Exemplo 05
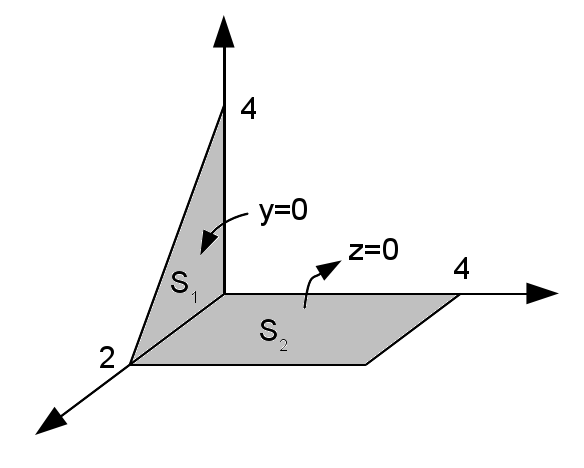
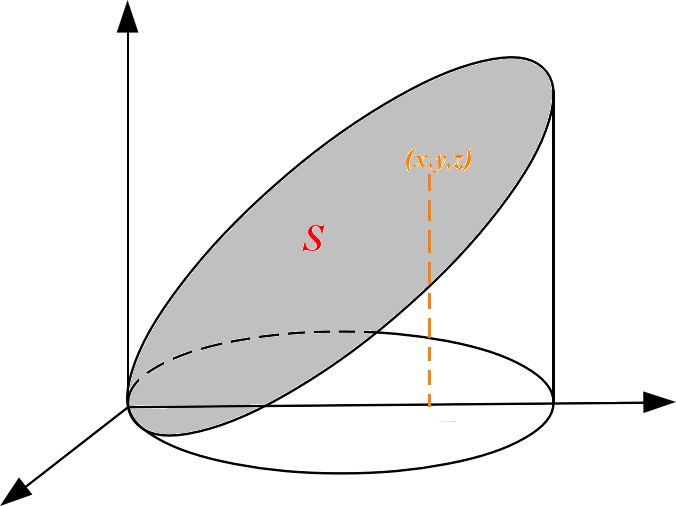
Calcular $\displaystyle \iint \left( x+y+z \right) \,d\sigma$, onde $S=S_1\cup S_2$ é a superfície
SOL.
\[ \begin{align*} I =& I_1 + I_2\\ I_1 =& \iint_{S_1} G(x,y,z)\,d\sigma\\ I_2 =& \iint_{S_2} G(x,y,z)\,d\sigma \end{align*} \] Vamos calcular $I_1$, neste caso a superfície está definida explicitamente pela equação $y = 0$: \[ \begin{align*} d\sigma =& \sqrt{\left( 1 + \dfrac{\partial y}{\partial x} \right)^2 + \left( \dfrac{\partial y}{\partial z} \right)^2 + 1\,\,\,}\,\,dx\,dz\\ d\sigma =& \sqrt{1+0+0\,\,\,}\,\,dx\,dy\\ d\sigma =& dx\,dy\\ \end{align*} \] Olhando para a figura notamos que o valor de $z$ está determinado pela escolha feita para o valor de $x$ via \[ z = 4 - 2x \nonumber \] dessa forma a nossa integral estará dada por \[ \begin{align*} I_1 & = \int_0^1 \int_0^{4-2x}\left( x+0+z \right) dx\,dy\\ &= \int_0^1 \left( 4-2x \right)\left[ x + \dfrac{1}{2}\left( 4-2x \right) \right] dx\\ &= 4\int_0^1 \left( 2-x \right) dx\\ &= 2\left. 4x - x^2\right|_0^1\\ &=8 \end{align*} \] Vamos calcular $I_2$, essa superfície está definida de forma explícita mediante a equação $z = 0$, dessa forma \[ \begin{align*} d\sigma =& \sqrt{ 1 + \left(\dfrac{\partial z}{\partial x} \right)^2 + \left( \dfrac{\partial z}{\partial y} \right)^2\,\,}\,\,dx\,dy\\ d\sigma =& \sqrt{1+0+0\,\,\,}\,\,dx\,dz\\ d\sigma =& dx\,dy\\ I_2 =& \int_0^4\int_0^2\left( x+y+z \right)\,dx\,dy\\ =& \int_0^4\int_0^2\left( x+y+0 \right)\,dx\,dy\\ =& \int_0^4 \left[\dfrac{x^2}{2} +yx\right]_0^2\,dy\\ =& \int_0^4 \left( 2 + 2y \right)\,dy\\ =&24 \end{align*} \]
Exemplo 06
Uma lâmina ter a forma de parte do plano $z=y$ recordada pelo cilindro $x^2+\left( y-1 \right) ^2=1$. Determinar a massa dessa lâmina, se a densidade de massa é proporcional à distancia desse ponto ao plano $xy$
)
SOL.
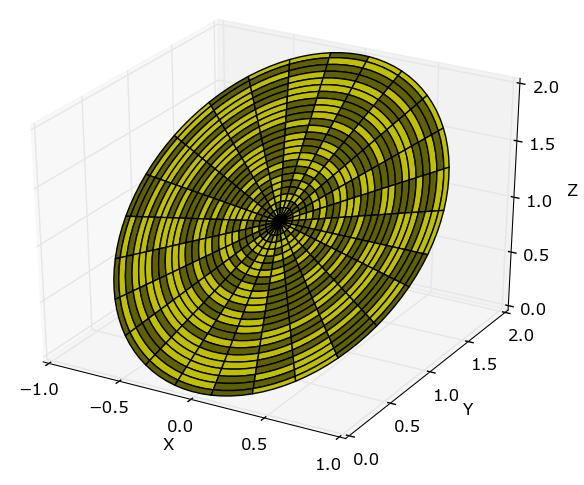
Temos pelo menos 2 abordagens para resolver esse problema, uma delas é parametrizar e a outra é considerar uma superfície definida de forma explícita. Vamos começar parametrizado
O plano, por outro lado, resulta da união de vários desses círculos, inciando com um de raio zero, até o final que tem a equação acima, isso se logra multiplicando por $v$ toda a equação e permitindo $0 \leq v \leq 1$: \[ \mathbf{r}(u,v) = v\cos u \,\mathbf{i} + v\left( 1+ \sin u \right) \,\mathbf{j} + v\left( 1+ \sin u \right) \,\mathbf{k} \nonumber \]
Dessa forma temos uma parametrização para o plano a partir da qual poderemos calcular a sua massa utilizando \[ m = \int \lambda (x,y,z) d\sigma \nonumber \] onde, para o nosso problema, $\lambda (x,y,z) = kz$. Com a escolha feita para representa a superfície, temos \[ d\sigma = \left| \, \mathbf{T}_u \times \mathbf{T}_v \, \right| dudv \nonumber \] onde \[ T_u \times T_v = \dfrac{\left( y,z \right)}{\left( u,v \right)}\,\mathbf{i} + \dfrac{\left( z,x \right)}{\left( u,v \right)} \,\mathbf{j} + \dfrac{\left( x,y \right)}{\left( u,v \right)} \,\mathbf{k} \nonumber \] com \[ \begin{align*} \dfrac{\left( y,z \right)}{\left( u,v \right)} &= v\cos u\left( 1-\sin u \right) -v\cos u\left( 1-\sin u \right) \\ & = 0\\ \dfrac{\left( z,x \right)}{\left( u,v \right)} &= v\cos u\left( \cos u \right) - \left( 1+\sin u \right)\left( -v\sin u\right)\\ &= v\cos^2u+v\sin u +v\cos^2u\\ &= v + v\sin u\\ \dfrac{\left( x,y \right)}{\left( u,v \right)} & = \left( 1+\sin u \right)\left( -v\sin u\right) - v\cos u\left( \cos u \right)\\ &=-v-v\sin u\\ \end{align*} \] dessa forma \[ d\sigma = v\sqrt{2}\sqrt{\left( 1+\sin u \right)^2}dudv = v\sqrt{2}\left( 1+\sin u \right)dudv \nonumber \] com isso podemos calcular a massa \[ \begin{align*} m &= \int_0^{2\pi} \int_0^1 v\sqrt{2}k\left( 1+\sin u \right)dudv\\ & = \sqrt{2}\,k\pi \end{align*} \]
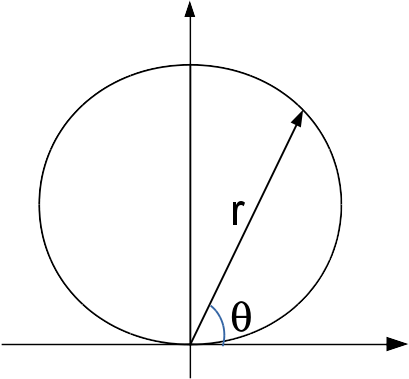
O outro método de solução é considerar a superfície definida de forma explícita, $z = y$, nesse caso \[ \begin{align*} d\sigma &= \sqrt{\left( \dfrac{\partial z}{\partial x} \right)^2 + \dfrac{\partial z}{\partial y} 1}dxdy\\ & = dxdy \end{align*} \] dessa forma, agora devemos realizar a integral respeitando os limites imposto pelo cilindro (e substituindo $z$ por $y$): \[ \begin{align*} m &= \iint_{0 \leq x^2 + \left( y -1 \right)^2 \leq 1}kzdxdy\\ & = \iint_{0 \leq x^2 + \left( y -1 \right)^2 \leq 1}kydxdy \end{align*} \] Vamos utilizar coordenadas polares, para isso devemos tentar descrever os limites imposto pelo cilindro ao plano. A figura que limita esse plano é a mostrada a seguir
)