Integral de Superfície de um campo vetorial

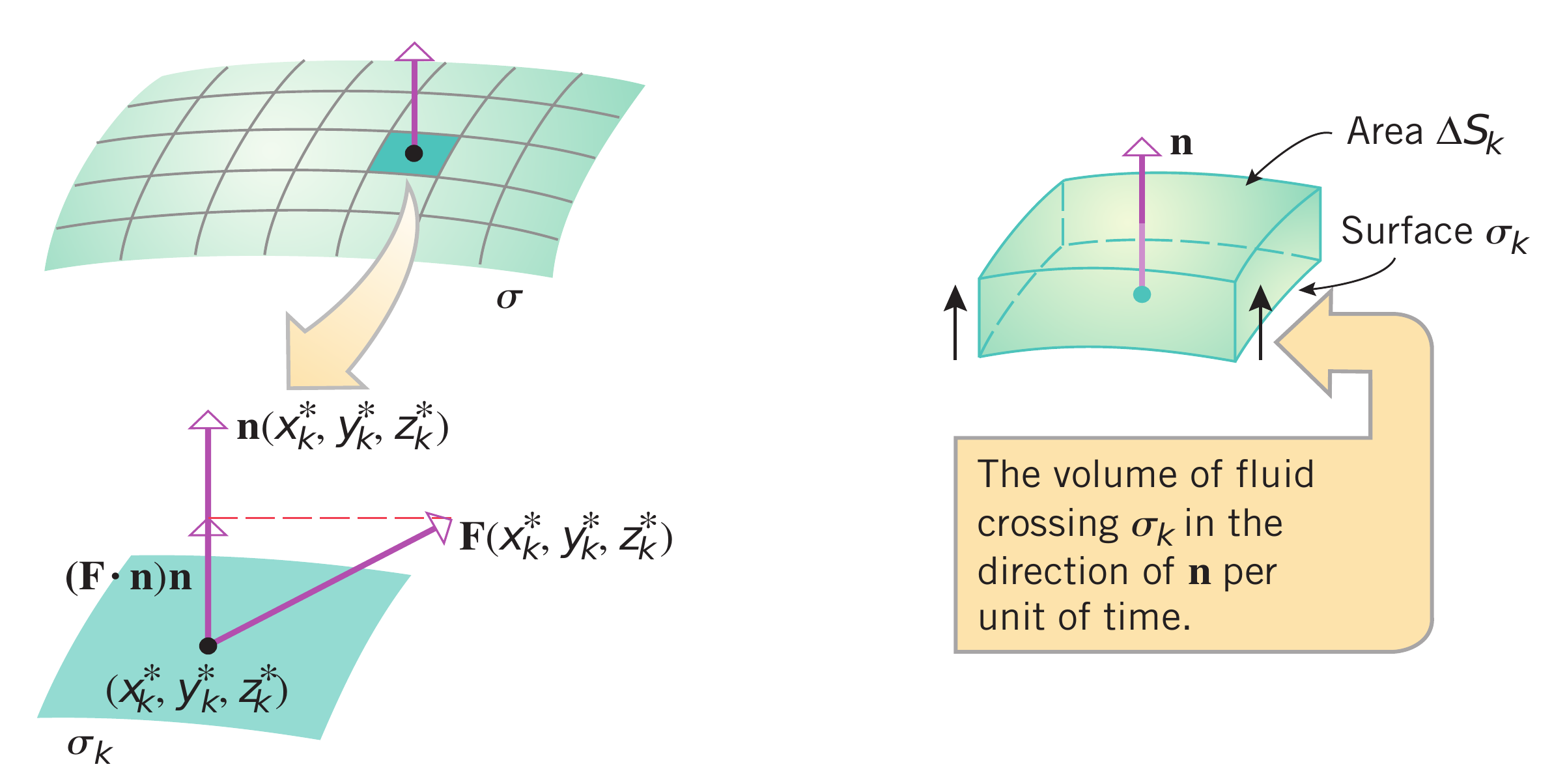
Vamos supor que $\mathbf{V}:\mathbb{R}^3\to \mathbb{R}^3$ é um campo (continuo) em $\mathbb{R}^3$ e $S$ é uma superfície simples. Se $F$ representa o campo de velocidades de um fluído (digamos que $ \mathbf{V} (\mathbf{r}_{0} )$ está dado em $m^3/s$). Queremos saber, quanto fluido por unidade de tempo atravessa a superfície $S$.

A fim de responder a essa pergunta vamos dividir a superfície $S$ em pequenos elementos de superfície de tamanho $\Delta \sigma$, observe que qualquer vetor $\mathbf{V}\left(\mathbf{r}_0\right)$ terá duas componentes, uma paralela ao plano tangente no ponto $\mathbf{r}_0$ e outra perpendicular ao plano tangente, por tanto a única componente de $\mathbf{V}$ capaz de atravessar a área $\Delta \sigma$ será \[ V_\perp = \left| \, \mathbf{V} \, \right|\, \cos \, \theta \nonumber \] onde $\theta$ é o ângulo entre $\mathbf{V}$ e o vetor normal à superfície, de fato, podemos escrever \[ V_\perp = \mathbf{V} \cdot \hat{\mathbf{n}} \nonumber \] em um intervalo de tempo $\Delta \, t$ o fluido que atravesso $S$ se deslocou uma distância de $\Delta l$ dada por \[ \Delta \, l_\perp = V_\perp \, \Delta \,t \nonumber \] se multiplicamos esse deslocamento pela área $\Delta \sigma$ teremos o volume de fluído que atravessou a superfície \[ \Delta \, Vol = V_\perp \, \Delta \,t\, \Delta \sigma \nonumber \]

dividindo tudo por $\Delta \,t$ teremos o volumem por unidade de tempo que atravessa o elemento de área $\Delta \sigma$, a essa grandeza chamaremos de fluxo, $\phi$, de forma que \[ \Delta \, \phi = \mathbf{V} \cdot \hat{\mathbf{n}} \, \Delta \sigma \nonumber \] somando todos os elementos de área e no limite em que estes são escolhidos suficientemente pequenos, teremos \[ \phi = \iint_S \,\mathbf{V} \cdot \hat{\mathbf{n}} \,d\, \sigma \nonumber \] A partir deste resultado estendemos o conceito de integral de campo vetorial para qualquer campo vetorial que atravesse a superfície $S$:

Definição

Seja $S$ uma superfície simples parametrizada por $\mathbf{r}:D[\mathbf{r}]\subset \mathbb{R}^2\to \mathbb{R}^3$, a qual proporciona uma orientação que coincide com a do campo de vetores normal $\mathbf{n}:D[\mathbf{r}] \to \mathbb{R}^3$. Seja $\mathbf{F}:D[\mathbf{F}]\subseteq \mathbb{R}^3\to \mathbb{R}^3$ um campo continuo definido no aberto $D[\mathbf{F}]$ de $\mathbb{R}^3$ o qual contem $D[\mathbf{r}]$. Se define a integral de superfície de $\mathbf{F}$ sobre $D[\mathbf{r}]$ (a qual chamaremos de fluxo de $\mathbf{F}$ através de $S$), denotada por $\displaystyle \iint_S \, \mathbf{F} \cdot d\mathbf{\sigma}$, onde \[ \phi_{\mathbf{F}} = \iint_S \, \mathbf{F} \cdot d\vec{\sigma} = \iint_{D[\mathbf{r}]} \, \mathbf{F} \cdot \hat{\mathbf{n}}\, d\sigma \nonumber \] onde, para o caso de uma superfície definida de forma vetorial temos \[ \begin{align*} d\sigma = & \left|\, \mathbf{T}_u \times \mathbf{T}_v \,\right|\,du\,dv\\ \hat{\mathbf{n}} =& \dfrac{\mathbf{T}_u \times \mathbf{T}_v}{\left|\, \mathbf{T}_u \times \mathbf{T}_v \,\right|\,du\,dv} \end{align*} \] se a superfície é definida de forma explícita, \[ d\sigma = \sqrt{\left( \dfrac{\partial F}{\partial x} \right)^2 + \left(\dfrac{\partial F}{\partial y} \right)^2 + 1\,\,\,}\,\,dx\,dy \nonumber \] e a orientação definida para cima (na direção do vetor unitário perpendicular à superfície projetada), teremos \[ \hat{\mathbf{n}} = \dfrac{-\dfrac{\partial F}{\partial x}\,\mathbf{i} - \dfrac{\partial F}{\partial y} \,\mathbf{j} + \,\mathbf{k}}{\sqrt{\left( \dfrac{\partial F}{\partial x} \right)^2 + \left(\dfrac{\partial F}{\partial y} \right)^2 + 1\,\,\,}} \nonumber \] se a orientação definida para baixo (na direção contraria do vetor unitário perpendicular à superfície projetada), teremos \[ \hat{\mathbf{n}} = \dfrac{\dfrac{\partial F}{\partial x}\,\mathbf{i} + \dfrac{\partial F}{\partial y} \,\mathbf{j} + \,\mathbf{k}}{\sqrt{\left( \dfrac{\partial F}{\partial x} \right)^2 + \left(\dfrac{\partial F}{\partial y} \right)^2 + 1\,\,\,}} \nonumber \] e se for definida de forma implícita \[ \begin{align*} d\sigma = & \dfrac{\left|\, \vec{\nabla}F \,\right|}{\left|\, \vec{\nabla}F\cdot \mathbf{p} \,\right|}\\ \hat{\mathbf{n}} =& \pm\dfrac{\vec{\nabla}F}{\left|\, \vec{\nabla}F \,\right|}\\ \end{align*} \]

Um exemplo desse tipo de integral que você já viu em Física é a Lei de Gauss \[ \iint_S \mathbf{E} \cdot d\vec{\sigma} = \dfrac{Q}{\epsilon_0} \nonumber \] onde $\mathbf{E}$ é o campo elétrico, $Q$ a carga dentro da superfície $S$, e $\epsilon_0$ é a permissividade do vácuo, dada por $8,8541878176\times 10^{-12}\dfrac{C^2}{N\,m^2}$, no SI, a qual indiretamente está relacionada com a forma com que um determinado médio ira responder à ação do campo elétrico (susceptibilidade elétrica).

Outra aplicação das integrais de superfícies sobre campos vetoriais é no estudo do fluxo de calor. Se existe uma diferencia de temperatura entre duas superfície teremos um fluxo de calor da região mais quente para aquela com menor temperatura a qual está dado por \[ \mathbf{q} = -k\,\vec{\nabla}T \nonumber \] onde $\vec{\nabla}T$ é o gradiente de temperatura que se estabelece entre as superfícies e $k$ é a condutividade térmica, a equação anterior é a equação de Fourier para a condução térmica a qual é análoga à lei de Ohm. A taxa de fluxo de calor está dada por \[ \begin{align*} \phi_q =& \iint_S \mathbf{q}\cdot d\vec{\sigma}\\ =& -\iint_S k\,\vec{\nabla}T\cdot d\vec{\sigma} \end{align*} \]

Devemos ter presente que a integral de superfície em campos vetoriais são invariante por reparametrização que não mude a orientação da superfície $S$, se a reparametrização muda a orientação da superfície o resultado será \[ \iint_{S_{\mathbf{r}_+}} \, \mathbf{F} \cdot d\vec{\sigma} = - \iint_{S_{\mathbf{r}_-}} \, \mathbf{F} \cdot d\vec{\sigma} \nonumber \] onde $\mathbf{r}_+$ é a parametrização com orientação positiva e $\mathbf{r}_-$ é a parametrização com orientação negativa.

Exemplo 01

Calcule o fluxo do campo vetorial \[ \mathbf{F}(x,y,z) =x \,\mathbf{i} + y \,\mathbf{j} + z \,\mathbf{k} \nonumber \] através da superfície de uma esfera de raio $a$ utilize coordenadas esférica para representar a superfície (parametrização do resto do mundo)

Exemplo 02

Repita o problema anterior considerando a parametrização da Diva.

Exemplo 03

Calcule o fluxo de $\mathbf{F}(x,y,z) =x\,\mathbf{k}$, se a superfície está representada pela parametrização \[ \mathbf{r}(u,v) = u^2\,\mathbf{i} + v \,\mathbf{j} + \left( u^3-v^3\right) \,\mathbf{k} \nonumber \] orientada para cima.

Exemplo 04

Calcule o fluxo do campo \[ \mathbf{F}(x,y,z) = y\,\mathbf{i} +x \,\mathbf{j} +z \,\mathbf{k} \nonumber \] e $S$ é a superfície externa da região sólida $E$ delimitada pelo paraboloide $z=1-x^2-y^2$ e o plano $z=0$

Exemplo 05

Calcule o fluxo de $\mathbf{F} = x \,\mathbf{j} $ através da superfície $S$ definida por $y=1=x^2+z^2$ para $1 \leq y \leq 5$ com $S$ orientada apontando na direção negativa de $y$.

Exemplo 06

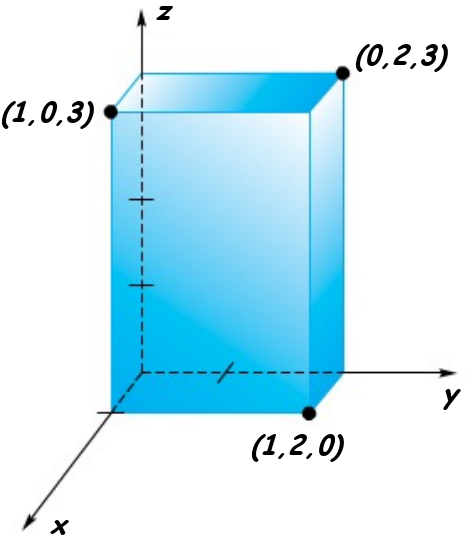
Calcule o fluxo do campo \[ \mathbf{F}(x,y,z) = x^2y\,\mathbf{i} + 2xz \,\mathbf{j} + yz^3 \,\mathbf{k} \nonumber \] através da superfície mostrada na figura ao lado.

Exemplo 07

A equação \[ z = 12,\;\;\;\;\;\;x^2+y^2\leq 25 \nonumber \] descreve um disco de raio $5$ que está no plano $z=12$. Suponha que o campo vetorial está dado por \[ \mathbf{F}(x,y,z) = x\,\mathbf{i} + y \,\mathbf{j} + z \,\mathbf{k} \nonumber \] calcule o fluxo do campo através da superfície.

Exemplo 08

A temperatura $T$ de uma esfera metálica é proporcional ao quadrado da distância ao centro da esfera. Calcule a taxa de fluxo de calor através da superfície da esfera se tem raio $a$.

Exemplos