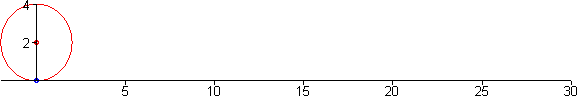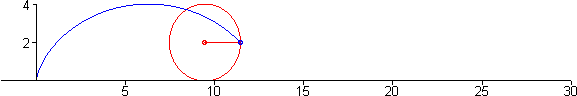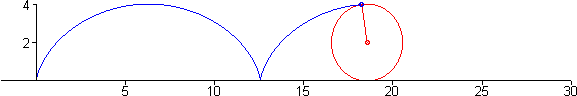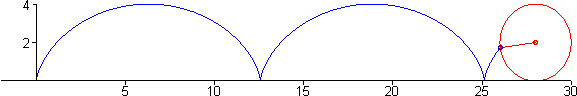Representação paramétrica de algumas curvas

Parametrização de uma Hélice

A fim de parametrizar a trajetória helicoidal devemos observar que essa curva projetada em algum plano ($xy$, $yz$ ou $zx$) forma uma circunferência, enquanto que quando projetada nos outros planos obtemos uma figura senoidal por exemplo, para o caso da figura mostrada acima temos que a figura que se forma no plano $xy$ ($z=0$) tem a seguinte equação vetorial $\mathbf{r}(t) = a \cos t \,\mathbf{i} + a \sin t\,\mathbf{j}$, onde $a$ é o raio da circunferência. No caso da projeção no plano $xz$ a equação da curva é a equação de uma função senoidal $\mathbf{r}(t) = a\sin\,t\,\mathbf{i} + m\,t \,\mathbf{k}$, por tanto, a partir destas equações obtemos que a equação da hélice circular é \[ \mathbf{r}(t) a \cos t \,\mathbf{i} + a \sin t\,\mathbf{j} + m\,t \,\mathbf{k};\;\;\;\; t\in\mathbb{R} \label{helice} \]

Parametrização de uma ciclóide

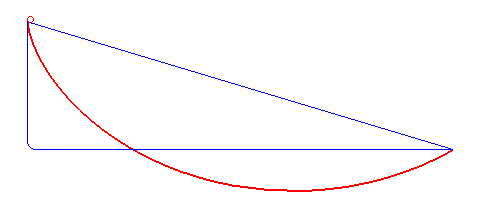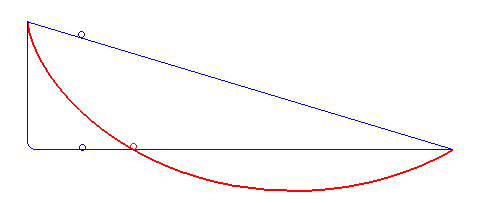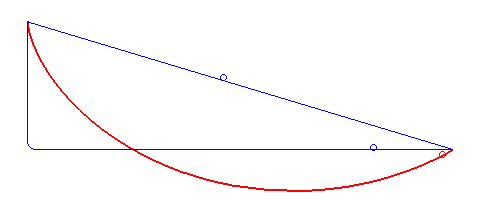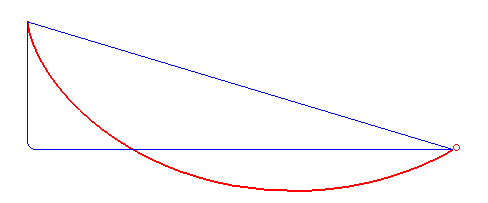
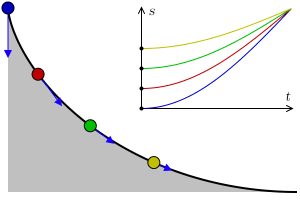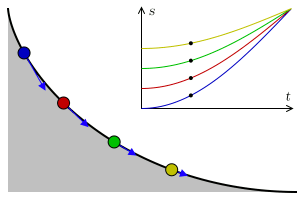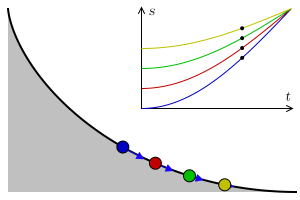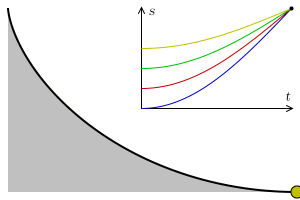
A ciclóide é a curva descrita por um ponto $P$ da circunferência de um círculo que se move ao longo de uma linha reta (ver figura acima). O ciclóide está relacionado a um dos problemas mais famosos da Física, o problema da braquistrócona

Em 1696, Johann Bernoulli apresento o problema da braquistrócona (), ele se perguntou sobre qual é a trajetória que um objeto deve seguir, sob a ação da gravidade, para que o tempo entre um ponto $A$ e outro ponto $B$ (sobre a curva) seja o mínimo dentro todas as curvas possíveis. O próprio Bernoulli mostrou que a trajetória coincide com a curva cicloide. Newton também aprentou uma solução e quando Bernoulli teve conhecimento exclamou: "conheço o leão pela pata" (figura acima retirada da Wikipedia).

Christian Huygens mostrou em 1673 que a ciclóide também é a solução ao Problema da Tautócrona: a curva descrita por uma partícula deslizando livremente sob a ação apenas da gravidade, atingindo o ponto de mínimo (o fundo da curva) no mesmo instante independente do ponto de partida na curva (figura acima retirada da Wikipedia).

Seja $a$ o raio da circunferência da figura acima. Nessa figura vemos que quando a circunferência gira um ângulo $t$, o centro se desloca uma distância $\overline{OT}$, que corresponde ao segmento de arco $\overset{\frown}{TP}$, que por definição é dado pelo produto do raio com ângulo $at$, isto é \[ \overline{OT}=\overline{PT}=at \nonumber \] note que \[ \begin{align*} x =& \overline{OT} - \overline{PA}\\ =& at - a\sin\, t\\ =& a\left(t- \sin\, t\right) \end{align*} \] igualmente \[ \begin{align*} y =& \overline{AT} \\ =& \overline{TC} - \overline{AC}\\ =& at - a\cos\, t\\ =& a\left(t- \cos\, t\right) \end{align*} \] dessa forma o vetor que descreve os pontos sobre o ciclóide está dado por \[ \mathbf{r}(t) = a\left(t- \sin\, t\right) \,\mathbf{i} + a\left(t- \cos\, t\right) \,\mathbf{j} \label{cicloide} \]

Parametrização de uma hipociclóide

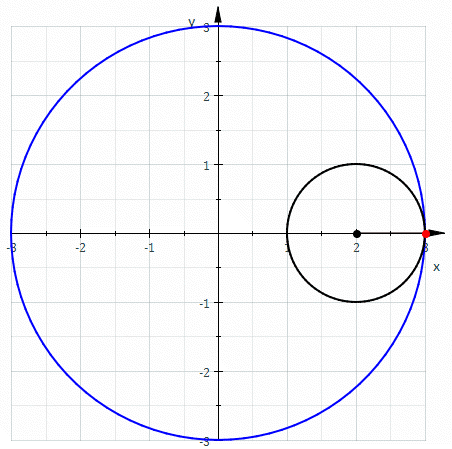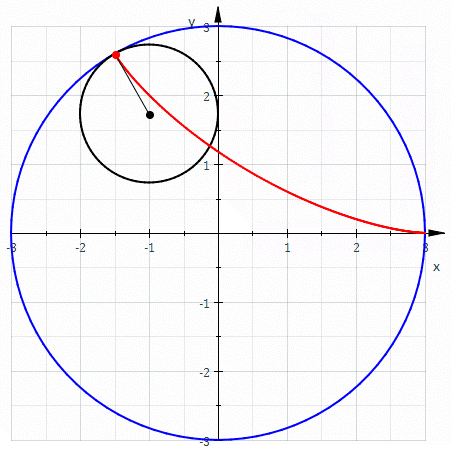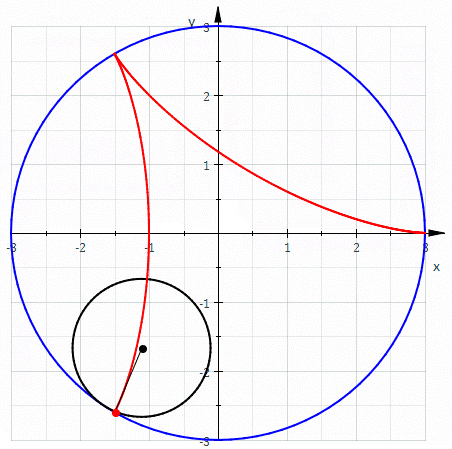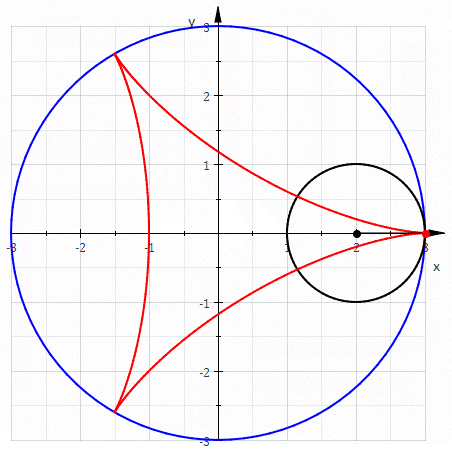
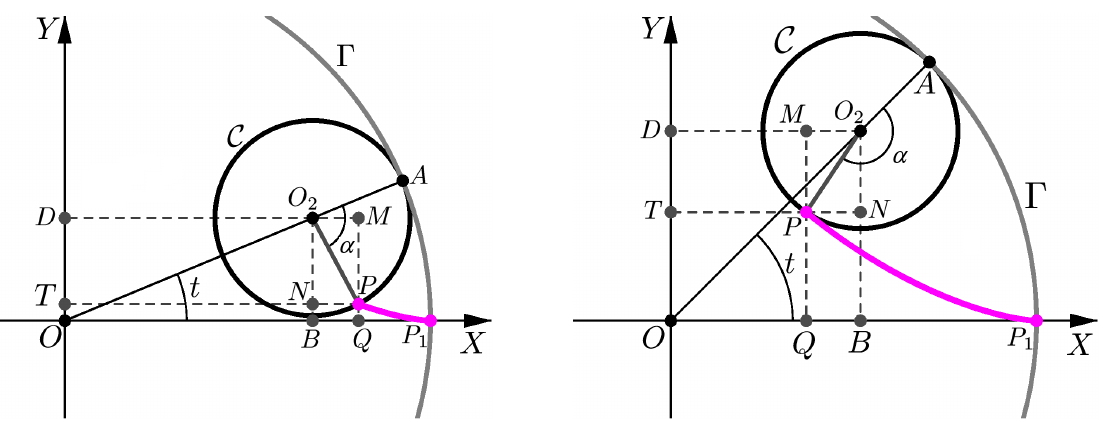
Se a trajetória seguida pela circunferência é outra circunferência de a figura resultante é um hipociclóide

A partir da figura acima temos \[ \begin{align*} x =& \overline{OQ}\\ =& \overline{OB} + \overline{QB}\\ =& \overline{OB} + \overline{O_2M} \end{align*} \] \[ \begin{align*} y =& \overline{OT}\\ =& \overline{OD} - \overline{TD}\\ =& \overline{OD} - \overline{O_2N} \end{align*} \] visto desde $O$, $O_2$ descreve uma circunferência de raio $b -a$, assim \[ \overline{OB} = \left(b-a \right)\cos\, t \nonumber \] \[ \overline{OD} = \left(b-a \right)\sin\, t \nonumber \] se $\alpha$ o ângulo entre $\overline{O_2A}$ e $\overline{O_2P}$, temos \[ \begin{align*} \widehat {NO_{2}P}&= \pi -\left[ \alpha +\dfrac {\pi } {2}-t\right]\\ &=\dfrac {\pi } {2}+\left( t-\alpha \right) \end{align*} \] Assim, no triangulo rectangulo $PNO_2$: \[ \begin{align*} \overline{O_2M} =& b \sin \, \left(\widehat {NO_{2}P} \right)\\ =& b\sin \, \left[ \dfrac {\pi } {2}+\left( t-\alpha \right) \right]\\ =& b\cos \, \left( t-\alpha \right) \end{align*} \] \[ \begin{align*} \overline{O_2N} =& b \cos \, \left(\widehat {NO_{2}P} \right)\\ =& b\cos \, \left[ \dfrac {\pi } {2}+\left( t-\alpha \right) \right]\\ =& b\sin \, \left( t-\alpha \right) \end{align*} \] Uma relação importante é que o arco descrito por $\alpha$ e $t$ são os mesmos \[ \begin{align*} b\alpha =& a\,t \alpha &= \dfrac{a}{b}t \end{align*} \] Assim \[ \widehat {O_{2}M} = b\cos \left[ \dfrac {a-b} {b}t\right] \nonumber \] \[ \widehat {O_{2}N} = b\sin \left[ \dfrac {a-b} {b}t\right] \nonumber \] de forma que \[ \begin{align*} x =& \overline{OB} + \overline{O_2M}\\ =& \left(b-a \right)\cos\, t + b\cos \left[ \dfrac {a-b} {b}t\right] \end{align*} \] \[ \begin{align*} y =& \overline{OD} - \overline{O_2N}\\ =& \left(b-a \right)\sin\, t - b\sin \left[ \dfrac {a-b} {b}t\right] \end{align*} \] de forma que a função vetorial que descreve a hipociclóide está dada por \[ \begin{align} \mathbf{r}(t) =& \left\{ \left(a - b \right)\cos\, t + b\cos \left[ \dfrac {a-b} {b}t\right] \right\} \,\mathbf{i} -\nonumber\\ &\left\{ \left(a-b \right)\sin\, t - b\sin \left[ \dfrac {a-b} {b}t\right] \right\} \,\mathbf{j} \label{hipocicloide} \end{align} \]

Aos pontos de contato da trajetória com a circunferência externa chamamos de cúpside. Para termos uma cúspide de se verificar \[ at = n\,2\pi b\;\;\;\;\;n=0,\, 1,\, 2,\, \ldots \nonumber \] de onde \[ t=2\pi n\dfrac {b} {a} \]

Um caso particular é a hipociclóide de 4 cúspides, ela acontece quando $t=2\pi$, assim \[ \begin{align*} 2\pi =& 8\pi \dfrac {b} {a}\\ b = \pi \dfrac {a} {4} \end{align*} \] para esse caso, a equação $\ref{hipocicloide}$ reduz para \[ \begin{align*} x =& \dfrac {a} {4}\left( 3\cos t+\cos 3t\right)\\ y =& \dfrac {a} {4}\left( 3\sin t-\sin 3t\right) \end{align*} \] como \[ \begin{align*} 1 - \cos \theta =& 2\cos^2 \dfrac{\theta}{2}\\ 1 - \cos 2\theta =& 2\cos^2 \theta\\ \left( 1 - \cos 2\theta \right) \cos \theta =& 2\cos^3 \theta\\ \cos \theta - \cos 2\theta \cos \theta =& 2\cos^3 \theta \end{align*} \] da mesma forma sabemos \[ \cos x\cos y=\dfrac {1} {z}\left[ \cos \left( x-y\right)+ \cos \left( x+y\right) \right] \nonumber \] aplicando este resultado na equação anterior obtemos que ($2\cos ^{2}x=1+\cos 2x$) \[ \begin{align*} \cos 2\theta \cos \theta =&\dfrac {1} {2}\left[ \cos \theta +\cos 3\theta \right]\\ \left(2\cos ^{2}x - 1 \right) \cos \theta =&\dfrac {1} {2}\left[ \cos \theta +\cos 3\theta \right]\\ 2\cos \theta +\cos \theta +\cos 3\theta =&4\cos^3 \theta\\ 3\cos \theta +\cos 3\theta =&4\cos^3 \theta \end{align*} \] como $\theta = \alpha + \dfrac{\pi}{2}$, então \[ \begin{align*} \cos \theta =& \cos \left( \alpha +\dfrac {\pi } {2}\right)\\ &=-\sin \alpha\\ \cos 3\theta =& \cos \left( 3\alpha +\dfrac {3\pi } {2}\right)\\ =& \sin 3\alpha\\ \cos ^{3}\left( x+\dfrac {\pi } {2}\right) =& -\sin ^3\alpha \end{align*} \] de forma que \[ -3\sin \alpha +\sin 3\alpha =-4\sin ^{3}\alpha \nonumber \] pelo que podemos escrever \[ \begin{align*} x =& a\cos ^3\,t\\ y =& a\sin ^3\,t \end{align*} \] de onde \[ \begin{align*} \left( \dfrac {x} {a}\right) ^{1 / 3}=\cos t \left( \dfrac {y} {a}\right) ^{1 / 3}=\sin t \end{align*} \] elevando as equações ao quadrado \[ \begin{align*} \left( \dfrac {x} {a}\right) ^{2 / 3}=\cos^2 t \left( \dfrac {y} {a}\right) ^{2 / 3}=\sin^2 t \end{align*} \] e somando, obtemos \[ \begin{align*} \left( \dfrac {x} {a}\right) ^{2 / 3} + \left( \dfrac {y} {a}\right) ^{2 / 3} =&1\\ x^{2/3} + y^{2/3} = & a^{2/3} \end{align*} \]

Parametrização de outras curvas

Como mencionado no inicio, as funções vetoriais permitem expressar diferentes tipos de curvas, em especial as curvas que resultam de interseções de superfícies, vejamos alguns exemplos de curvas que são parametrizadas utilizando funções vetoriais

exemplo 01

Escreva a equação vetorial para $y=5x+3$ no plano $z=2$.

exemplo 02

A interseção da superfície $z=x^2+y^2$ e $z=2+y$ determina uma curva, encontre a equação vetorial dessa curva.

Exemplo 03

Representar parametricamente a curva dada pela interseção das superfícies $x+y=2$ e $x^2+y^2+z^2=2(x+y)$

Exemplo 04

Esboce a curva obtida pela interseção do semi elipsoide \[ \dfrac {x^{2}} {12}+\dfrac {y^{2}} {24}+\dfrac {z^{2}} {4}=1,\;\;\;\;z\geq 0 \nonumber \] e o cilindro parabólico $\displaystyle y=x^2$. Encontre a função vetorial que descreve a curva

Exemplo 05

Parametrize a curva resultante da interseção do plano $x+2y+4z=4$ e o cilindro elítico $x^2 + 4y^2=4$

Exemplos