Derivada direcional
Conceito de Campo
Antes de introduzir o conceito de deriva direcional e gradiente devemos definir os entes matemáticos sobre os quais estes conceitos (operadores) atuaram, nos referimos aos campos, os quais pode ser vetoriais ou escalares
Campo Escalar
| Definição campo escalar |
|
Um campo escalar e um mapeamento definido por \[ f:A\subseteq \mathbb{R}^m \to \mathbb{R} \nonumber \] O que significa dado uma $m-tupla$ de conjunto $A$, $f$ é a função que associa a cada ponto do espaço $m$ dimensional um número real |
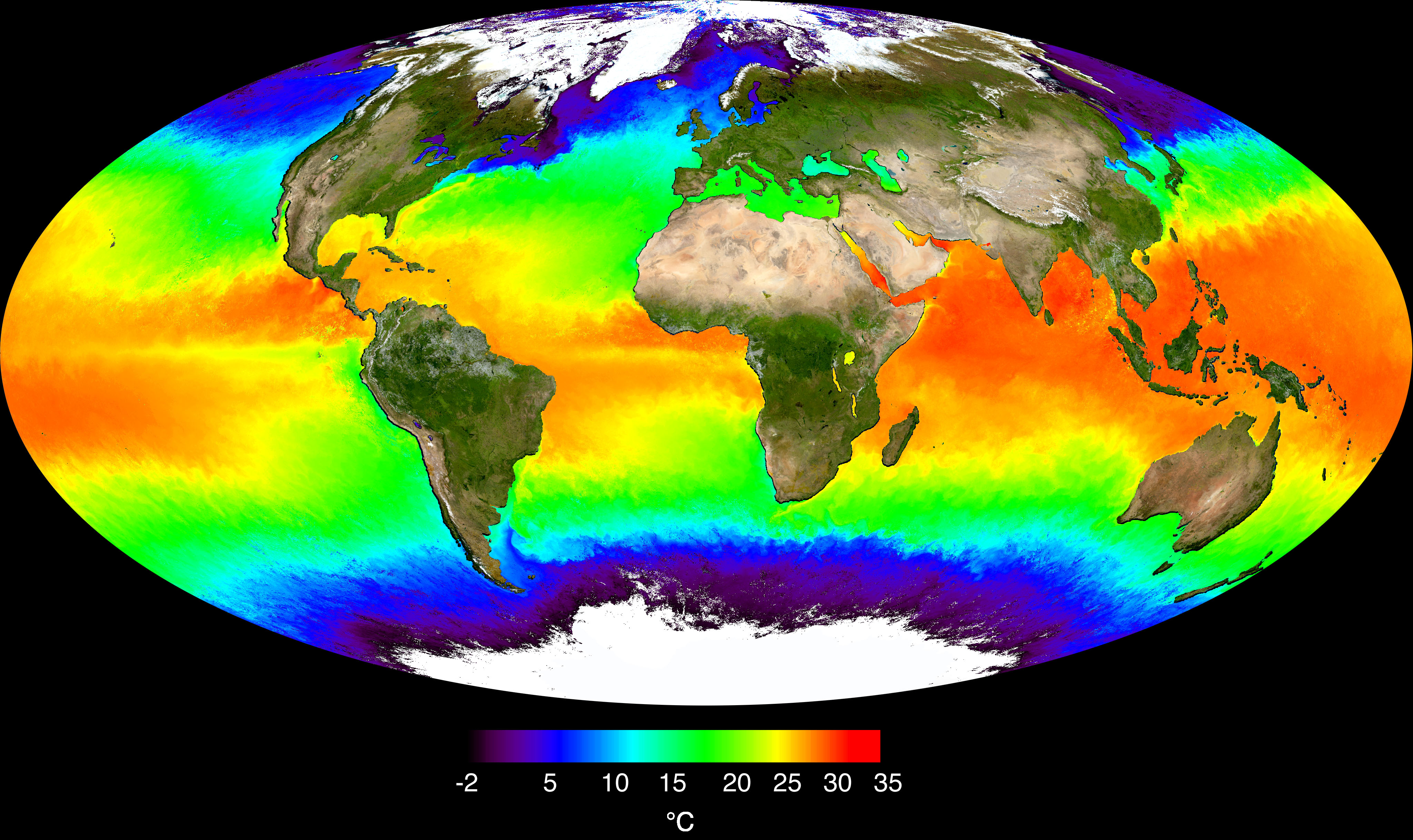
O exemplo típico são os campos de temperatura muitos utilizadas por meteorologistas.
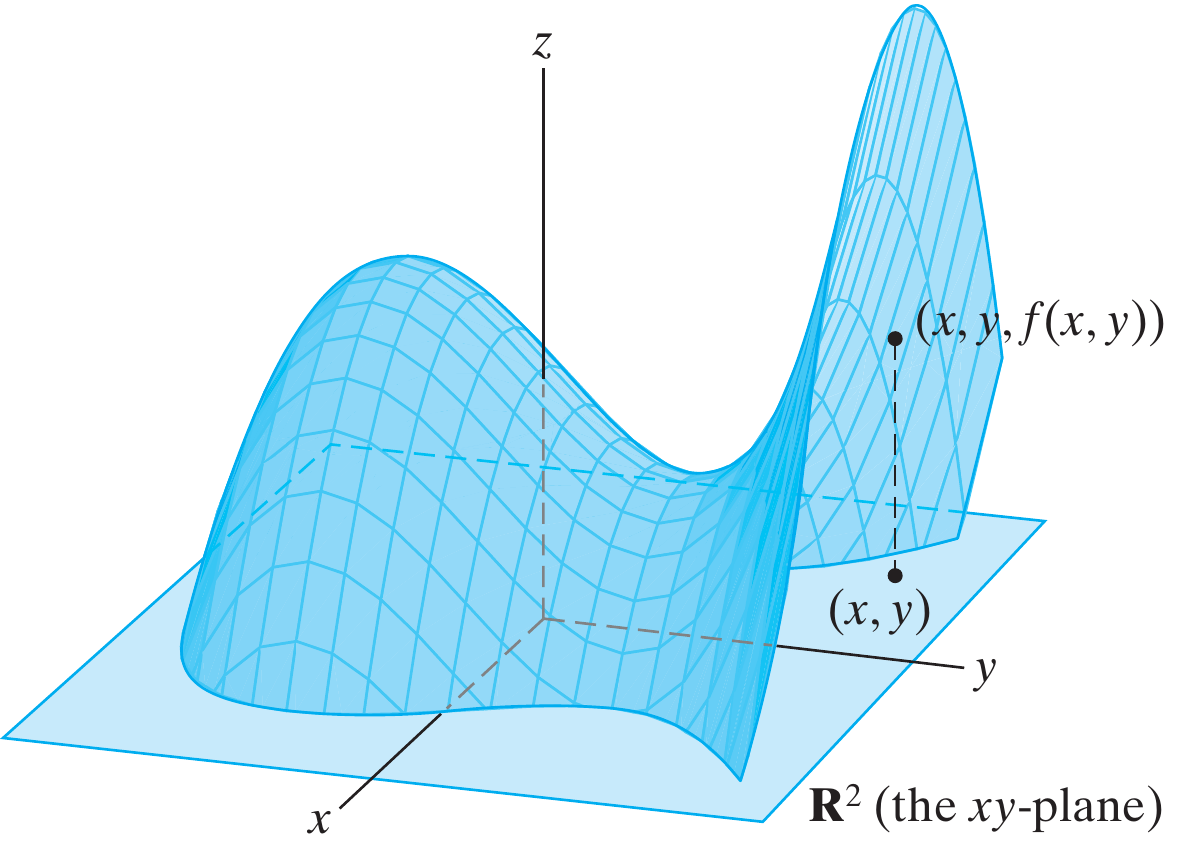
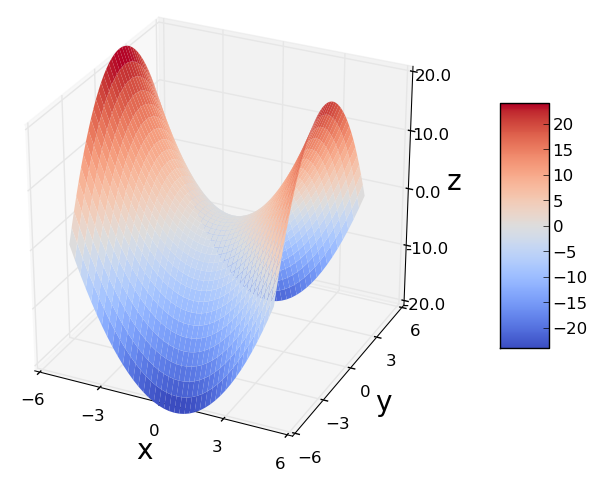
Na figura acima temos a representação gráfica do campo de temperatura da superfície dos oceanos. Então resulta evidente que este campo é um mapeamento do tipo $\displaystyle f:A\subseteq \mathbb{R}^2 \to \mathbb{R}$ onde para cada ponto da superfície dos mares ($\mathbb{R}^2$) atribuímos uma temperatura ($\mathbb{R}$). Desta figura também nos mostra uma forma os campo escalares do tipo $\displaystyle f:X\subseteq \mathbb{R}^2 \to \mathbb{R}$ via um mapa de colores, outra forma de expressar graficamente os campos escalares desse tipo é utilizando gráficos em 3D, onde o para cada par ordenado $(x,y)$ a função associa um valor $z$, isto é $f=\left\{z \in Z \,|\, z=f(x,y),\,\forall (x,y) \in A\right\}$.
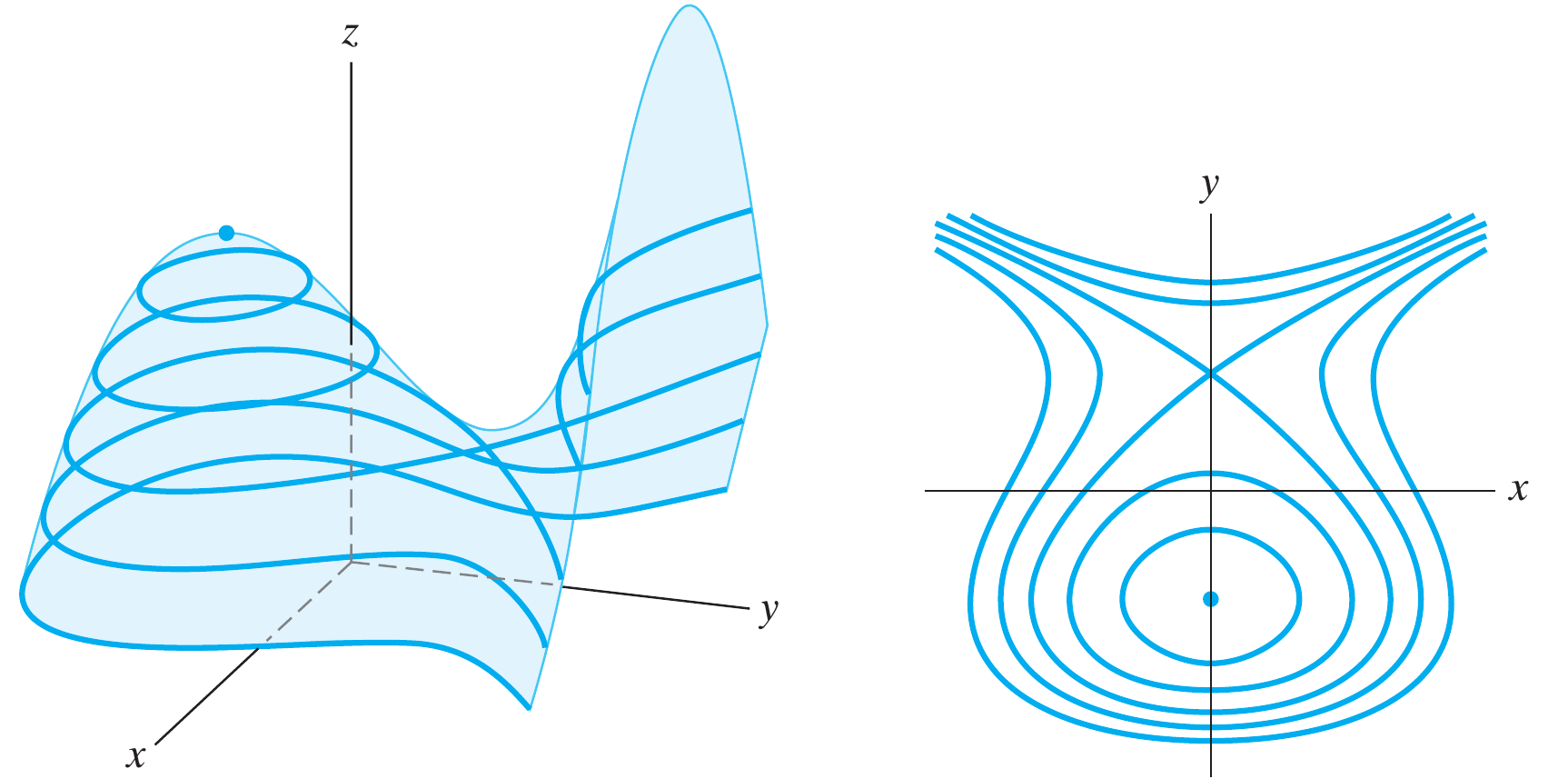
As duas últimas representações são equivalente pois o código de colores utilizado na primeira figura é escolhido segundo o valor da variável $z$. Uma outra representação equivalente é a obtida via as curvas de níveis
| Definição |
|
Seja $\displaystyle f:A\subseteq \mathbb{R}^2 \to \mathbb{R}$ uma função que representa um campo escalar. As curvas de níveis de altura $c$ de $f$ são as curvas definidas pela equação $f(x,y)=c$, onde $c$ é uma constante. Em notação matemática \[ \text{curva de nivel de altura c = }\left\{ (x,y)\in \mathbb{R}^2\,\left|\; f(x,y)=c\right. \right\} \nonumber \] A curva de contorno à altura $c$ de $f$ é a curva em $\displaystyle \mathbb{R}^3$ definida por as duas equações $z=f(x,y)$ e $z=c$: \[ \text{curva de contorno à altura c = }\left\{ (x,y,z)\in \mathbb{R}^3\,\left|\, z=f(x,y)=c\right. \right\} \nonumber \] |
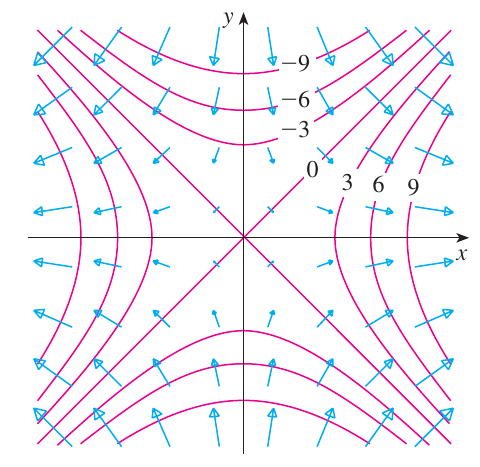
Quando as curvas de contorno são projetadas no plano $xy$ obtemos um mapa de contorno, o qual é similar ao mapa de corres mostrado na primeira figura.
Exemplo 01
Um tanque $T$ tem forma de um cilindro circular reto de raio $1\,m$ e altura de $3\,m$. O tanque está cheio de uma substancia líquida. Cada partícula dessa substância está sujeita a uma pressão que é proporcional à distância da partícula até a superfície livre do líquido. Usando coordenadas cartesianas, definir uma função escalar que descreva o campo de pressão no interior de $T$.
Campo vetorial
| Definição de campo vetorial |
|
Um campo vetorial em $\mathbb{R}^n$ é um mapeamento tal que \[ \mathbf{f}:A\subseteq \mathbb{R}^m \to \mathbb{R}^n \nonumber \] O que significa dado uma $m-tupla$ de conjunto $A$, $f$ é a função que associa a cada ponto do espaço $m$ dimensional um número vetor de $n$ componentes. |
Um exemplo típico deste tipo de campo é a descrição da velocidade das diversas partículas que conformam uma corrente de água (um rio fluindo, por exemplo). Uma observação importante a ser realizada é que as componentes do campo vetorial são campos escalares.
Exemplo 02
Dada a função $\mathbf{r}(x,y) = x \,\mathbf{i} + y \,\mathbf{j}$, desenhe o campo resultante.
Derivada direcional
Antes de introduzir o conceito de derivada direcional vamos relembrar o que é a derivada parcial de uma função escalar $z=f(x,y)$. Por definição as derivada parciais de $f$ estão dadas por \[ f_x =\dfrac {\partial f} {\partial x}=\lim _{\Delta x\rightarrow 0}\dfrac {f\left( x+\Delta x,y\right) -f\left( x,y\right) } {\Delta x},\;\;\;\;\;\;\;\;\;f_y =\dfrac {\partial f} {\partial y}=\lim _{\Delta y\rightarrow 0}\dfrac {f\left( x,y+\Delta y\right) -f\left( x,y\right) } {\Delta y} \nonumber \]
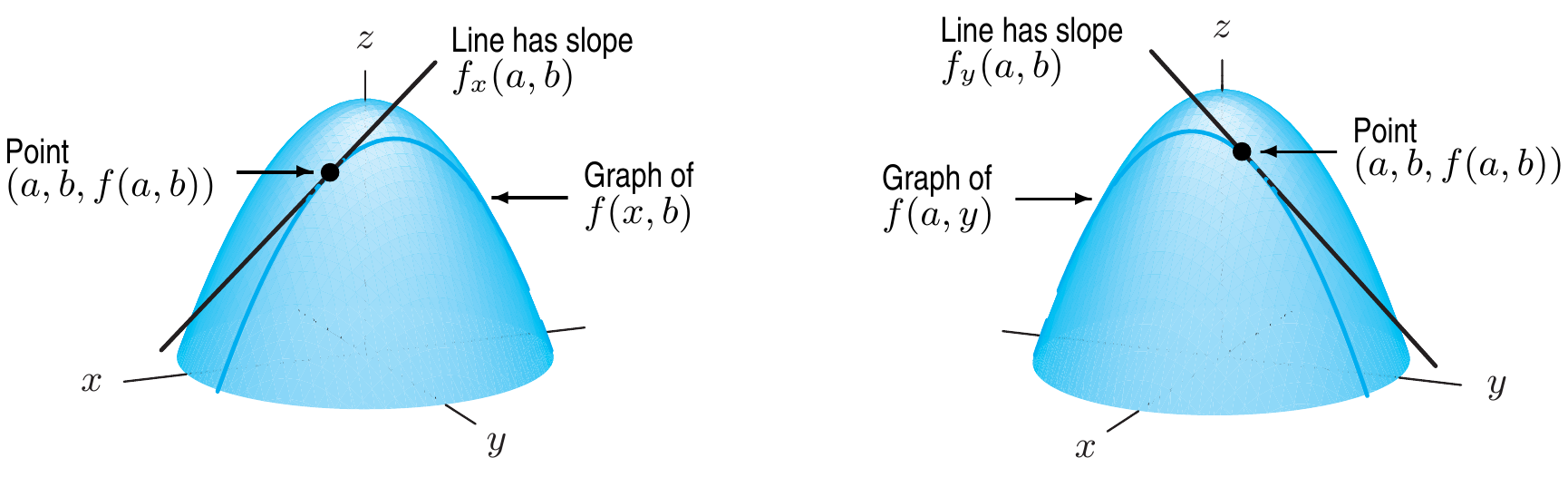
Do ponto de vista geométrico sabemos que as derivadas parciais de uma função são as inclinações das retas tangentes que estão na direção dos eixos coordenados. O problema com esta aproximação é que em varias situações devemos saber qual é a taxa de variação da curva em uma direção diferente à estabelecida pelos sistema de coordenadas.
Um exemplo dessa situação é a figura acima, suponha que está sobre uma montanha, qual é o caminho de deve ser tomado a fim de percorrer a menor distância, dito de outra forma, que direção deve ser seguida de forma que a variação $\Delta z$ seja maior. Da figura vemos que isto não acontece nem ao longo de $x$ nem ao longo de $y$, pare estar a uns $30^\circ$ do $\mathbf{x}$.
A partir da figura acima podemos dar uma definição para a derivada direcional de uma função.
| Definição |
|
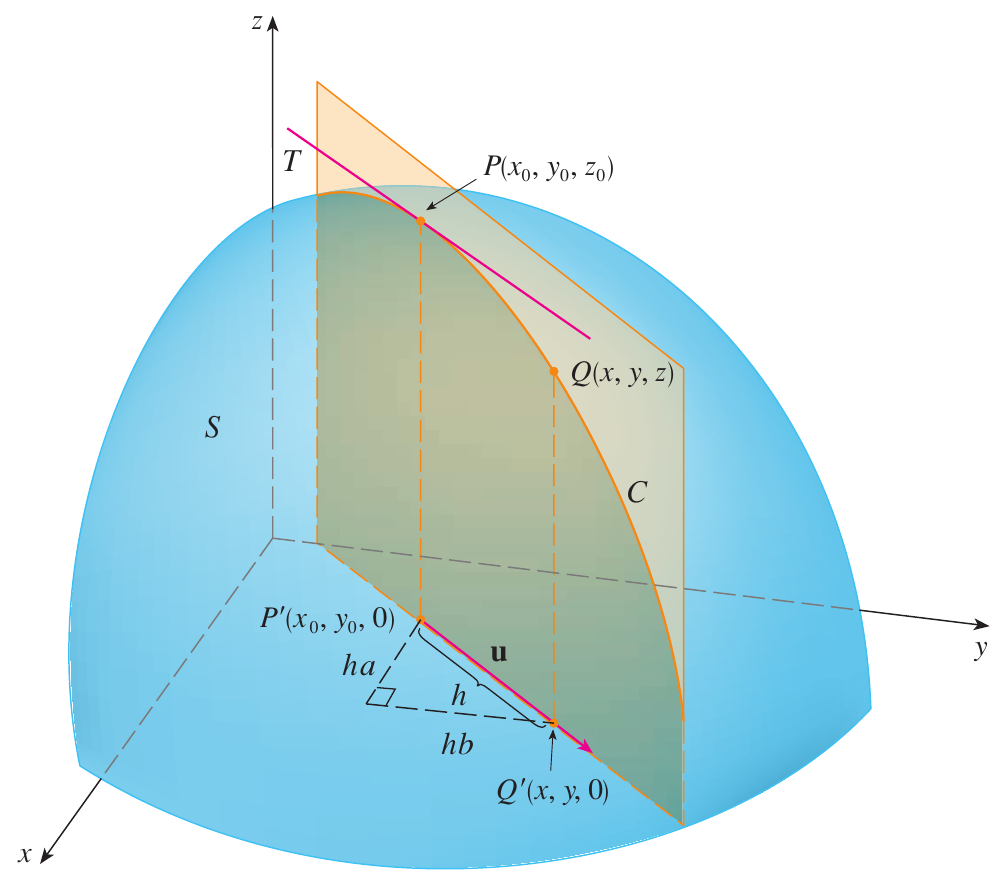
A derivada direcional de $f$ em $\left(x_0,\, y_0\right)$ na direção do vetor unitário $\mathbf{\hat{u}}=\left< a, b \right>$ é \[ D_{\mathbf{u}} = \lim _{h\rightarrow 0}\dfrac {f\left( x_{0}+ha,\,y_{0}+hb\right) -f\left( x_{0},\,y_{0}\right) } {h} \nonumber \] |
Esta não é a única definição que pode ser dada para a derivada direcional. A escolha por vetores unitários é a adequada dado que somente estamos interessados na sua direção e não na sua magnitude
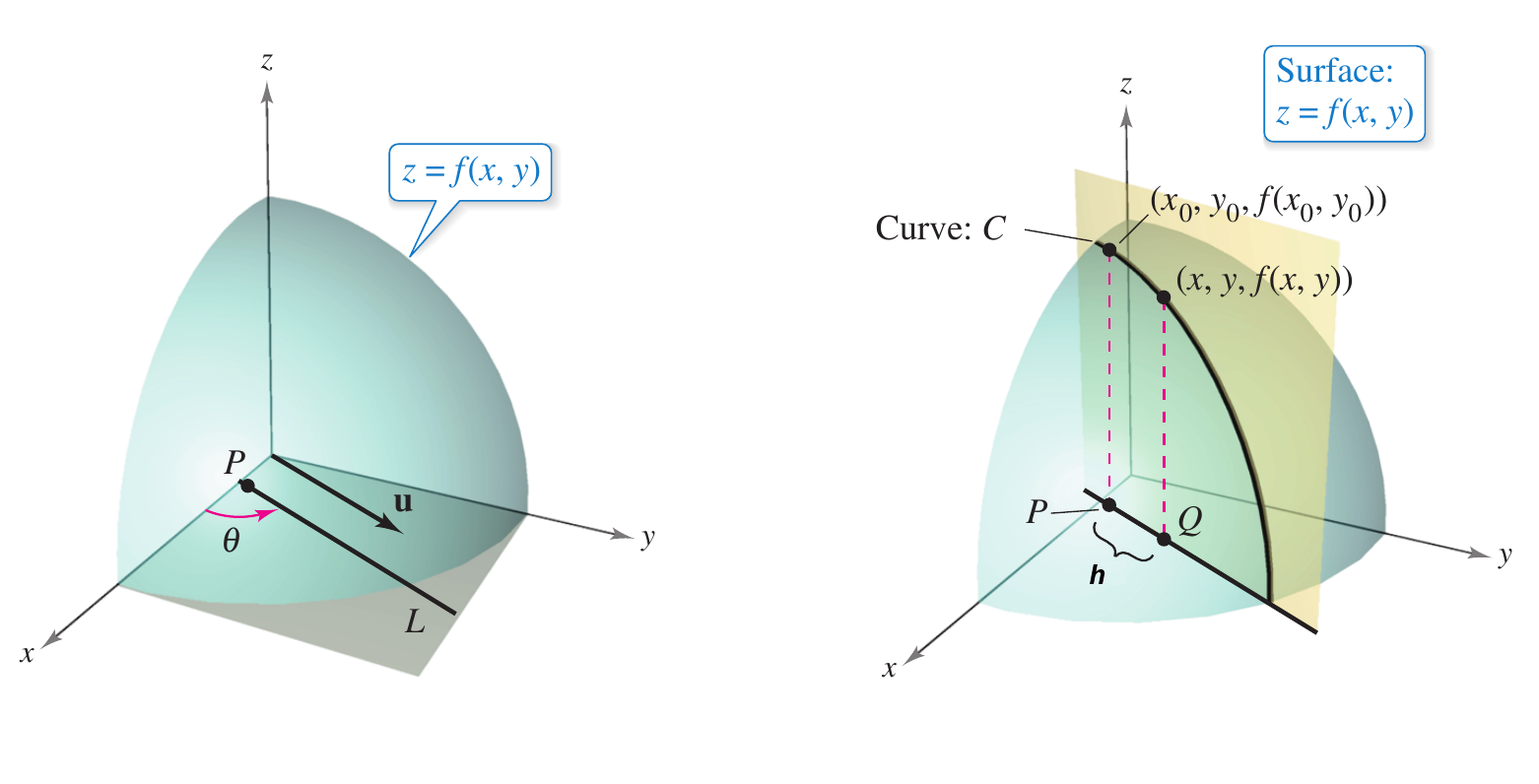
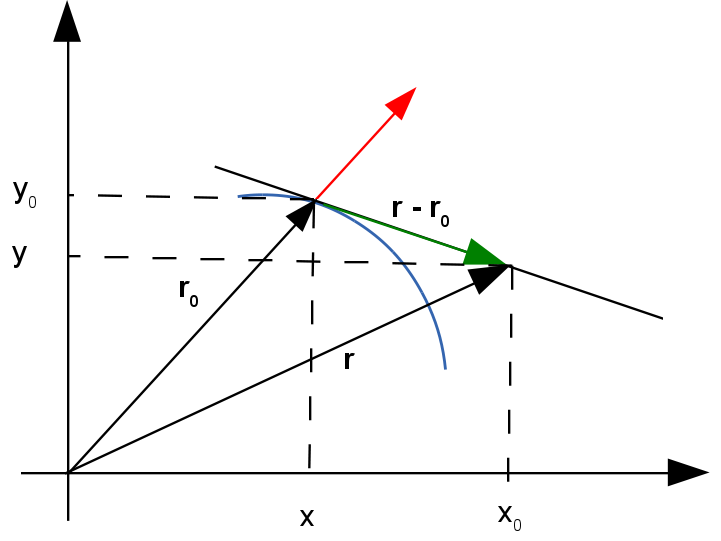
A partir de figura acima vemos que um vetor qualquer que passa pelos pontos $\left(x_0,\, y_0 \right)$ e $\left(x,\, y \right)$ define um ângulo em relação ao eixo $x$ o qual chamaremos de $\theta$, seja $c$ o comprimento do segmento $\bar{PQ}$, de forma que a posição do ponto $\left(x,\, y \right)$ está dada por \[ \begin{align*} x =& x_0 + h\,\cos \theta\\ y =& y_0 + h\,\sin \theta \end{align*} \] do anterior vemos que podemos reescrever a definição de derivada direcional como \[ D_{\mathbf{u}} = \lim _{h\rightarrow 0} \dfrac {f \left( x, \, y \right) -f\left( x_0,\,y_0 \right) } {h} = \lim _{h\rightarrow 0} \dfrac {f \left(x_0 + h\,\cos \theta ,\, y_0 + h\,\sin \theta \right) -f \left( x_0,\,y_0 \right) } {h} \nonumber \] Observe que se redefinimos $g(h) = f(x,y)$ então aplicando a regra da cadeia temos \[ \begin{array}{cclcl} g'(h) &=& f_x(x,y)\,x(h) &+& f_y(x,y)\,y(h)\\ g'(h) &=& f_x(x,y)\,\cos \theta &+& f_y(x,y)\, \sin \theta \nonumber \end{array} \] onde admitimos que quando $h=0$ então $x(0) = x_0$ e $y(0) = y_0$, a partir disso a definição de derivada da função anterior é \[ \begin{align*} g'(0) =& \lim_{h\to 0} \dfrac{g(h) - g(0)}{h}\\ =& \lim _{h\rightarrow 0} \dfrac {f \left(x_0 + h\,\cos \theta ,\, y_0 + h\,\sin \theta \right) -f \left( x_0,\,y_0 \right) } {h} \end{align*} \] o que nos leva a uma outra definição de derivada direcional
| Teorema |
|
Se $f$ é uma função diferenciável de $x$ e $y$, então a derivada direcional de $f$ na direção de $\mathbf{\hat{u}} =\cos \theta \,\mathbf{i} + \sin \theta \,\mathbf{j}$ é \[ D_{\mathbf{u}} = f_x(x,y) \cos \theta + f_y(x,y) \sin \theta \nonumber \] |
Gradiente e a derivada direcional
Dessa definição observamos que a derivada direcional pode ser escrita: \[ \begin{align*} D_{\mathbf{u}} =& f_x(x,y) \cos \theta + f_y(x,y) \sin \theta\\ =& \left[\cos \theta \,\mathbf{i} + \sin \theta \,\mathbf{j} \right] \cdot \left[ f_x(x,y) \,\mathbf{i} + f_y(x,y) \,\mathbf{j} \right]\\ =& \mathbf{\hat{u}} \cdot \mathbf{\nabla} f \end{align*} \] onde $\mathbf{\nabla}$ é o operador diferencial nabla ou del e à operação $\mathbf{\nabla} f$ se conhece como gradiente de $f$:
| Definição de Gradiente |
|
Se $f$ é uma função de 2 variáveis $x$ e $y$ e $f_x(x,y)$ e $f_y(x,y)$ existen, então o gradiente de $f$, denotado por $\mathbf{\nabla} f$ (le-se "del f" ou "grad f") está definido por \[ \mathbf{\nabla} f = \dfrac{\partial f}{\partial x} \,\mathbf{i} + \dfrac{\partial f}{\partial y} \,\mathbf{j} \nonumber \] |
De posse dessa definição podemos reescrever a derivada direcional como
|
\[ D_{\mathbf{u}} = \mathbf{\hat{u}} \cdot \mathbf{\nabla} f \nonumber \] |
O gradiente possui propriedades interessantes que serão uteis na realização de resolução de problemas relacionados com máximos e mínimos da derivada direcional
| Propriedades do gradiente |
|
Seja $f$ uma função diferenciável no ponto $(x,y)$.
|
Demonstração: Se $\mathbf{\nabla} f = \mathbf{0}$, então para qualquer direção (qualquer $\mathbf{\hat{u}}$) temos \[ \begin{align*} D_{\mathbf{u}}f(x,y) =& \mathbf{\nabla} f(x,y) \cdot \mathbf{\hat{u}}\\ =& \left(0 \,\mathbf{i} +0 \,\mathbf{j}\right) \cdot \left(\cos \theta \,\mathbf{i} + \sin \theta \,\mathbf{j} \right)\\ \mathbf{0} \end{align*} \] Se $\mathbf{\nabla} f \neq \mathbf{0}$, seja $\phi$ o ângulo entre $\mathbf{\nabla} f(x,y)$ e $\mathbf{\hat{u}}$, então, por definição \[ \begin{align*} D_{\mathbf{u}}f(x,y) =& \mathbf{\nabla} f(x,y) \cdot \mathbf{\hat{u}}\\ =& \left| \mathbf{\nabla} f(x,y) \right| \cdot \left| \mathbf{\hat{u}} \right| \cos \phi\\ =& \left| \mathbf{\nabla} f(x,y) \right|\cos \phi \end{align*} \]
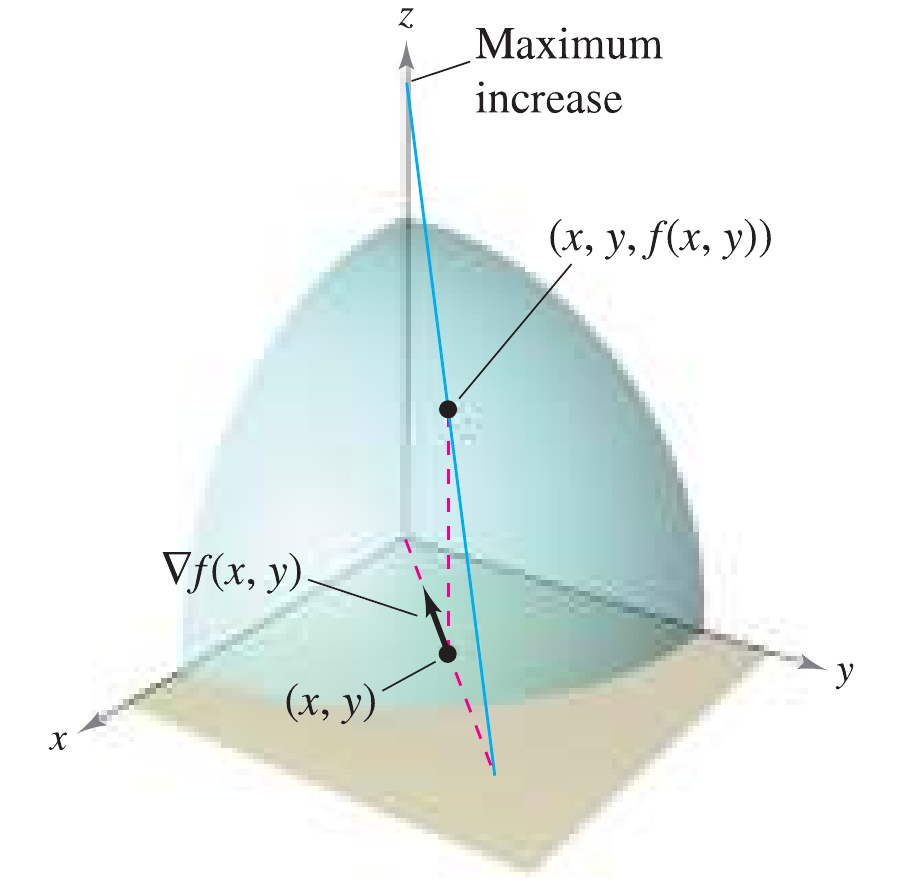
disto vemos que o máximo de $D_{\mathbf{u}}f(x,y)$ acontece quando $\cos \phi = 1$, o que implica que $\phi = 0$, dessa forma vemos que o máximo valor da derivada direcional é obtida quando o gradiente tem a mesma direção que $\mathbf{\hat{u}}$. Disto também vemos que o maior valor assumido pela derivada direcional $D_{\mathbf{u}}f(x,y)$ é precisamente \[ \left|\mathbf{\nabla} f(x,y) \right|\cos \phi = \left|\mathbf{\nabla} f(x,y) \right| \nonumber \] Isso pode ser entendido vendo a figura ao lado, note que o valor de $f(x,y)$, visto desde o plano $xy$, aumenta até atingir se máximo valor em $z=0$.Propriedades geométricas do gradiente
A definição a seguir deixa claro o significado geométrico do gradiente
| Normal |
|
Se $f$ é uma função diferenciável no ponto $(x_o, y_o)$ e $\mathbf{\nabla} f \neq \mathbf{0}$, então $\mathbf{\nabla} f(x_o, y_o)$ é normal à curva no ponto $(x_o, y_o)$. |
Demonstração: Vamos supor uma curva $S$ representada pela equação cartesiana $F(x,y)=k$. Seja $P(x_0,y_0)$ um ponto sobre $S$. Suponha que essa curva é parametrizada com o parâmetro $t$ e que o ponto $P(x_0,y_0)$ está determinado pelo vetor $\mathbf{r}(t_0) = x_0\,\mathbf{i} + y_0\,\mathbf{j}$, isto é \[ F\left(x(t),y(t)\right)=k \nonumber \] se $x$ e $y$ são funções diferenciáveis, então é verdade que (regra da cadeia) \[ \dfrac{\partial F}{\partial x}\dfrac{dx}{dt} + \dfrac{\partial F}{\partial y}\dfrac{dy}{dt} + \dfrac{\partial F}{\partial z}\dfrac{dz}{dt} = 0 \nonumber \] como \[ \mathbf{\nabla} F(x,y) = \dfrac{\partial F}{\partial x} \,\mathbf{i} + \dfrac{\partial F}{\partial y} \,\mathbf{j} \nonumber \] e \[ \mathbf{r}'(t) = \dfrac{dx}{dt}\,\mathbf{i} + \dfrac{dy}{dt}\,\mathbf{j} \nonumber \] então \[ \mathbf{\nabla} F(x,y) \cdot \mathbf{r}'(t) = 0 \nonumber \] particularmente isto é verdade para \[ \nonumber \mathbf{\nabla} F(x_0,y_0) \cdot \mathbf{r}'(t_0) = 0 \]
De fato, o gradiente nos da a direção da normal à curva no ponto $P_0$, mas como a normal é por definição perpendicular à tangente à curva podemos calcular o valor desta última utilizando o gradiente. Para ver isso analisemos a seguinte figura
Seja o vetor em vermelho o resultante do gradiente da função escalar. Da figura é claro que
| Tangente à curva |
|
Se $\mathbf{r} - \mathbf{r_0}$ é perpendicular a $\mathbf{\nabla}\,f(P_0)$, então \[ \mathbf{\nabla}\,f(P_0)\cdot\left( \mathbf{r} - \mathbf{r_0} \right) = \mathbf{0} \nonumber \] |
Interpretação Física do gradiente
Assim o gradiente de um campo escalar é um campo vetorial. Se $\phi$ for um campo escalar e $\mathbf{F}$ o campo vetorial definido por $\mathbf{F}= \mathbf{\nabla} \phi$, então $\mathbf{F}$ será chamado de campo vetorial gradiente e $\phi$ será denominado função potencial para $\mathbf{F}$. Um campo vetorial gradiente também é chamado de campo conservativo e entenderemos o porque depois.
Linhas de contorno e o gradiente
Quando trabalhamos com funções de duas variáveis, o gradiente sempre vai indicar a direção do máximo (ou mínimo), assim se nos traçamos uma projeção da figura no plano poderemos indicar em que direção as linhas de contorno aumentam, como mostrado nas figuras acima
Funções de 3 variáveis
Todo o dito até aqui referente as funções de duas variáveis pode ser estendido de forma natural para funções de 3 ou mais variáveis. O problema maior é que a interpretação da derivada direcional perde o sentido nesses casos, então vamos a fazer a extensão:
Sea $f$ uma função de $x$, $y$, $z$, com primeiras derivadas parciais contínuas. A derivada direcional de $f$ na direção do vetor unitário $\mathbf{\hat{u}} = a\,\mathbf{i} +b \,\mathbf{j} + c \,\mathbf{k}$ está dada por
\[
D_\mathbf{\hat{u}}(x,y,z) = af_x(x,y,z) + bf_y(x,y,z) + cf_z(x,y,z)
\nonumber
\]
o gradiente de $f$ está definido por
\[
\mathbf{\nabla} f (x,y,z) = f_x(x,y,z)\,\mathbf{i} + f_y(x,y,z\,\mathbf{j}) + f_z(x,y,z\,\mathbf{k})
\nonumber
\]
As propriedades do gradiente são as seguintes
Exemplos
Exemplo 03
Seja $f(x,y) = xe^y$ $P=(2,-1)$ e $\mathbf{u}=< 2,3 >$, calcule a derivada direcional de $f$ ao longo de $\mathbf{u}$ avaliada no ponto $P$.
Exemplo 04
\[ f(x,y) = \dfrac{x^2}{10} - \dfrac{y^2}{9} \nonumber \] (a) Determine o gradiente de $f$ em $R = (4,3)$. Utilize o gradiente para calcular a derivada direcional de $R$ na direção de $R$ para $Q=(5,6)$
Exemplo 05
A temperatura na superfície de um metal está dada por (em graus Celsius); \[ f(x,y) = 20 - 4x^2 - y^2 \nonumber \] onde $x$ e $y$ estão medidos em centímetros. Em que direção no ponto $(2,-3)$ a temperatura aumenta mais rapidamente. Qual é a taxa de incremento?
Exemplo 06
Uma partícula está localizada no ponto $(2,-3)$ sobre uma superfície metálica aquecida à temperatura dada por \[ T(x,y) = 20 - 4x^2 - y^2 \nonumber \] Encontre o caminho que a partícula deve seguir a fim de atingir o ponto mais quente da superfície.
Exemplo 07
Esboce a curva de nível para $c=0$ da função dada por \[ f(x,y) = y - \sin x \nonumber \] e encontre os vetores normais em vários pontos da curva
Exemplo 08
Encontrar a equação da reta tangente à curva $x^2+y^2=4$ no ponto $\left( \sqrt{3}, 1 \right)$, utilizando o gradiente.
Exemplo 09
Considere uma carga elétrica positiva $Q$, situada na origem de um plano $xy$, conforme a figura conforme a figura. Sabendo que as curvas equipotenciais são descritas por circunferências em torno da carga e tem valor dado por \[ V = \dfrac{Q}{r}, \nonumber \] calcule o campo vetorial, $\mathbf{E}$, associado ao campo escalar.