Integral de linha de campos vetoriais
Podemos estender o conceito de integral de linha estudado nas aulas anteriores para o caso em que a função peso é uma função vetorial, para esses casos definimos a integral de linha vetorial como
| Definição |
|
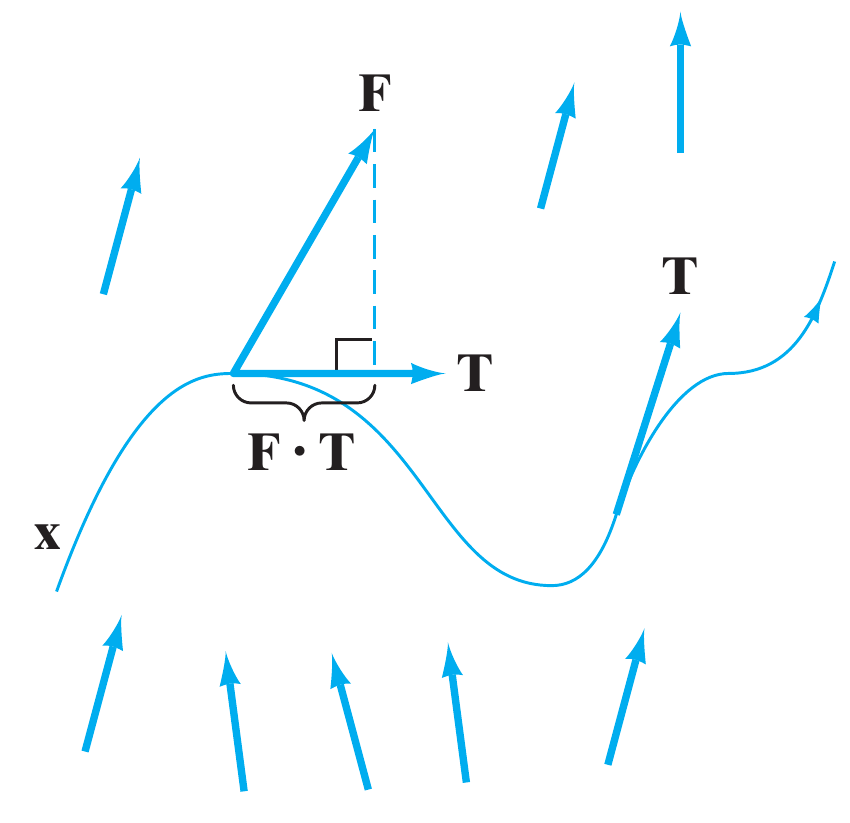
Seja $\displaystyle \mathbf{r}:[a,b]\to \mathbb{R}^n$ um campo vetorial de classe $C^1$ ($n$ é $2$ ou $3$ para nosso estudo). Seja $\mathbf{F}$ definido num conjunto $X$ de $\mathbb{R}^n$ tal que $R$ contenha as imagens $\mathbf{r}$, Assuma que $\mathbf{F}$ varia continuamente ao longo de $\mathbf{r}$. A integral de lina de $\mathbf{F}$ ao longo de $\mathbf{r}:[a,b]\to \mathbb{R}^n$, denotada por $\displaystyle \int_{C} \mathbf{F}\cdot d\mathbf{r}$, e dada por \[ \int_{C} \mathbf{F}\cdot d\mathbf{r} = \int_{C} \mathbf{F}\left( \mathbf{r}(t) \right)\cdot \mathbf{v}(t)\,dt \nonumber \] |
A integral de linha vetorial mantém as mesmas propriedades que a integral de linha escalar exceto da última propriedade que é modificada:
| Propriedades |
|
|
Uma forma alternativa de apresentar a integral de linha é a seguinte \[ d\mathbf{r} = dx\,\mathbf{i} + dy \,\mathbf{j} + dz \,\mathbf{k} \nonumber \] e \[ \mathbf{F}(x,y,z) = f(x,y,z) \,\mathbf{i} + g(x,y,z) \,\mathbf{j} + h(x,y,z) \,\mathbf{k} \nonumber \] então
| Definição |
|
\[ \begin{align*} \int_C \,\mathbf{F}(x,y,z)\cdot\,d\mathbf{r} =& \int_C \left( f(x,y,z) \,\mathbf{i} + g(x,y,z) \,\mathbf{j} + h(x,y,z) \,\mathbf{k}\right) \cdot \left( dx\,\mathbf{i} + dy \,\mathbf{j} + dz \,\mathbf{k} \right)\\ =&\int_C f(x,y,z)\, dx + g(x,y,z)\, dy + h(x,y,z)\, dz \end{align*} \] |
Aplicações
Igualmente podemos recordar que o vetor tangente está definido como \[ \begin{align*} \mathbf{\hat{T}} =& \dfrac{\mathbf{v}}{\left|\mathbf{v}\right|}\\ =& \dfrac{d\mathbf{r}}{ds} \end{align*} \] (já que $s=\int \left|\mathbf{v}\right|\, dt$) onde $\mathbf{r}$ está parametrizado em termos do comprimento de arco. Com isso em mente
\[ \begin{align*} \int_{C} \mathbf{F}\cdot d\mathbf{r} =& \int_{C} \mathbf{F}\cdot \mathbf{v}\,dt\\ &= \int_{C} \mathbf{F}\cdot \dfrac{\mathbf{v}}{\left|\mathbf{v}\right|}\,\left|\mathbf{v}\right|\, dt\\ &= \int_{C} \mathbf{F}\cdot \mathbf{\hat{T}} \,\left|\mathbf{v}\right|\, dt\\ &= \int_{C} \mathbf{F}\cdot \mathbf{\hat{T}} \, ds \end{align*} \] Dessa forma, como $\mathbf{F}\cdot \mathbf{\hat{T}}$ é uma grandeza escalar, escrevemos a integral vetorial de linha como uma integral de linha escalar.
Circulação
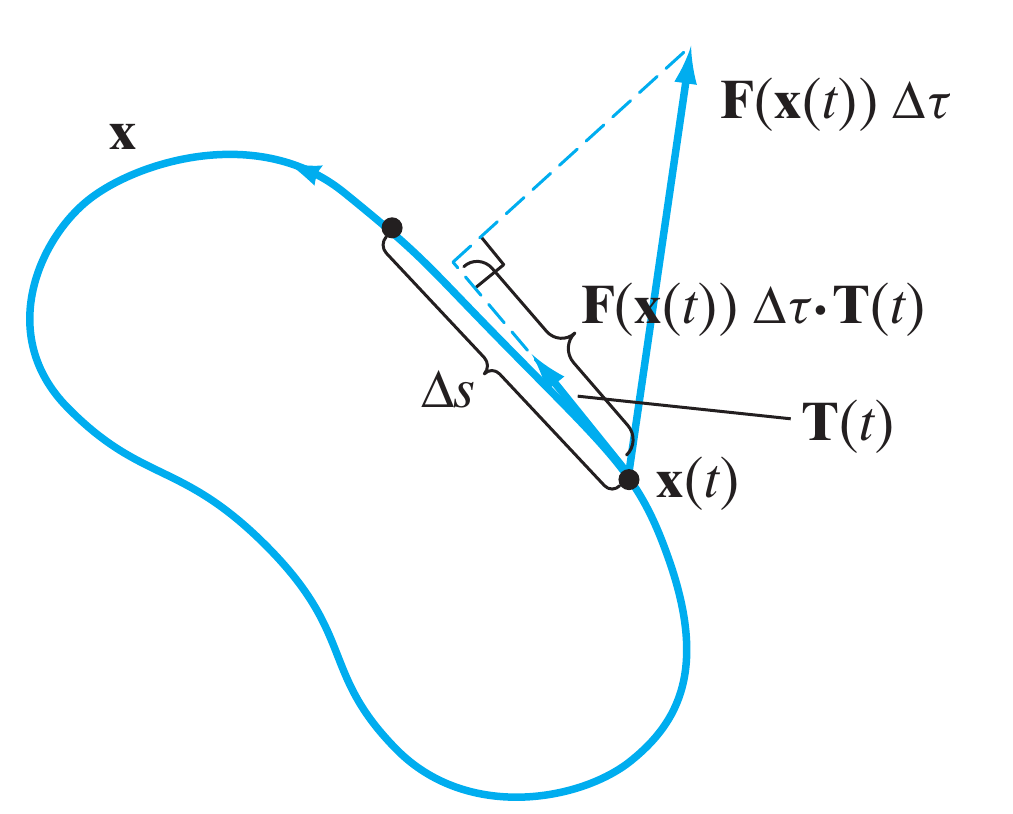
Una interpretação da integral de linha acontece quando $\mathbf{r}$ é um caminho fechado (isto é, quando $\mathbf{r}(a) = \mathbf{r}(b)$). Em esta circunstancia, a quantidade $\int_{C} \mathbf{F}\cdot d\mathbf{r}$ é chamada de circulação de $\mathbf{F}$ ao longo de $\mathbf{r}$. Para entender esta ideia melhor, suponha que $\mathbf{F}$ representa o campo de velocidades de um fluído. Considere uma quantidade de fluído que se move tangencialmente ao longo de um caminho $\mathbf{r}$ durante um breve intervalo $\Delta \tau$, como $\mathbf{F}\cdot \mathbf{\hat{T}}$ da a componente tangencial de $\mathbf{F}$, temos que
\[ \Delta L = \text{quantidade de fluído }\approx \left( \mathbf{F}\left( \mathbf{r}(t)\right)\Delta \tau \cdot \mathbf{\hat{T}}(t) \right) \Delta\, s \nonumber \] de onde \[ \dfrac{\Delta L}{\Delta \tau} \approx \left( \mathbf{F}\left( \mathbf{r}(t)\right) \cdot \mathbf{\hat{T}}(t) \right) \Delta\, s \nonumber \] Aplicando o limite em que $\Delta \tau \to 0$ e aplicando a soma de Riemman levando a partição para zero temos que \[ \dfrac{d L}{d \tau} = \int_c \left( \mathbf{F} \cdot \mathbf{\hat{T}} \right) ds = \int_c \mathbf{F} \cdot d\mathbf{s} \nonumber \]
Trabalho
Agora vamos ver as aplicações da integral de linha, esse tipo de integrais são bem conhecidas na Física: considere $\mathbf{F}$ como sendo um campo de forças no espaço, a integral $\displaystyle \int_{C} \mathbf{F}\cdot d\mathbf{r}$ representa o trabalho feito por $\mathbf{F}$ sobre a partícula quando se move ao longo $\mathbf{r}$
| Definição |
|
\[ W = \int_{C} \mathbf{F}\cdot d\mathbf{r} \nonumber \] |
Independência do caminho de integração
Existem funções que a integral de linha só depende dos pontos extremos do caminho, estas funções são funções que derivam de potenciais gradiente definidos num espaço simplesmente conexo ou seja, são campos conservativos:
| Definição |
|
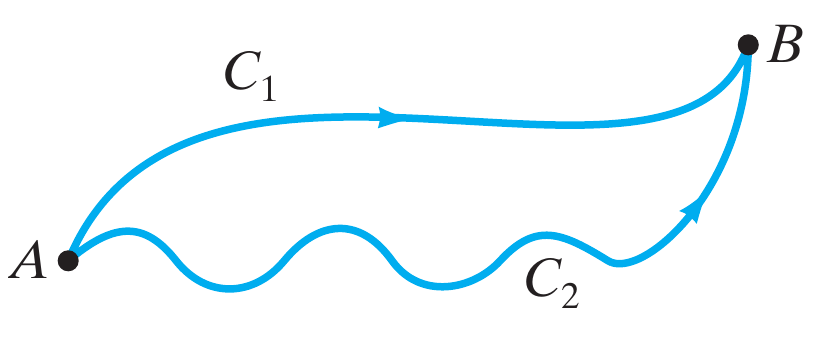
Um campo vetorial $\mathbf{F}$ tem uma integral de linha independente do caminho se \[ \int_{C_1} \mathbf{F} \cdot d\mathbf{s} = \int_{C_2} \mathbf{F} \cdot d\mathbf{s} \nonumber \] para duas curvas orientadas simples, definidas por partes de classe $C^1$, quaisquer definidas no domínio de $\mathbf{F}$ e que tem o mesmos pontos inicial e final. |
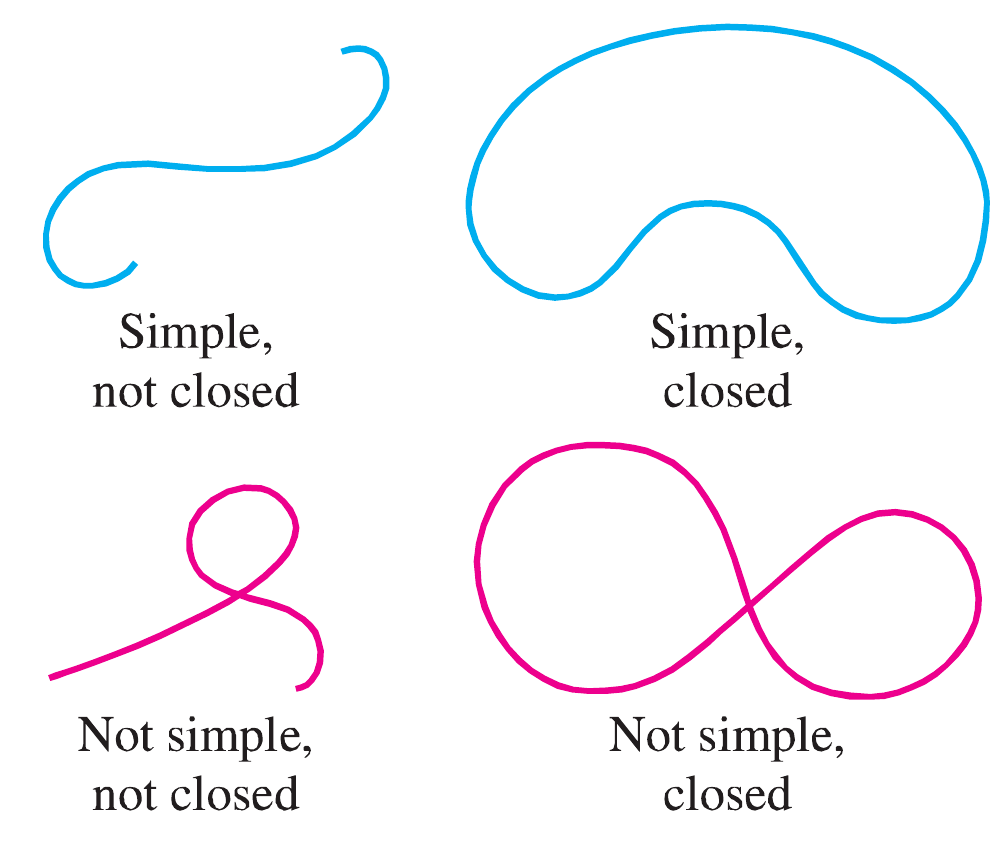
A partir dessa definição podemos dizer que qualquer campo vetorial, $\mathbf{F}$, contínuo será independente de caminho de integração se e somente se \[ \oint \mathbf{F} \cdot d\mathbf{s} = 0 \nonumber \] para toda curva simples, fechada e definida por partes de classe $C^1$, definida no domínio de $\mathbf{F}$.
Campos Conservativos
Por definição um campo conservativo é aquele que além de outras propriedades verifica \[ \mathbf{F} = \vec{\nabla} f \nonumber \] por tanto \[ \begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{s} =& \int_a^b \vec{\nabla} f\left( \mathbf{r}(t) \right) \cdot d\mathbf{s}\\ =& \int_a^b \vec{\nabla} f\left( \mathbf{r}(t) \right) \cdot \mathbf{v}\,dt\\ \end{align*} \] da regra da cadeia sabemos \[ \dfrac{d\,}{dt}f\left( \mathbf{r}(t) \right) = \vec{\nabla} f\left( \mathbf{r}(t) \right)\cdot \mathbf{v}(t) \nonumber \] por tanto \[ \begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{s} =& \int_a^b \vec{\nabla} f\left( \mathbf{r}(t) \right) \cdot \mathbf{v}\,dt\\ =& \int_a^b \dfrac{d\,}{dt}f\left( \mathbf{r}(t) \right)\,dt\\ =& \left. f\left( \mathbf{r}(t) \right) \, \right|\,_a^b\\ =& f\left( \mathbf{r}(b) \right) - f\left( \mathbf{r}(a) \right) \end{align*} \] a partir deste resultado apresentamos o seguinte teorema
| Teorema |
|
Seja $\mathbf{F}$ definida num conjunto $R$ aberto, continuo e conexo o qual é subconjunto de $\mathbb{R}^n$. Então $\mathbf{F}=\vec{\nabla} f$ (onde $f$ é uma função de classe $C^1$ definida em $R$) se e somente se $\mathbf{F}$ tem a integral de linha independe do caminho sobre curvas definidas em $R$. Além disso, se $C$ é qualquer curva orientada de classe $C^1$ definida por partes, definida em $R$ com o ponto inicial $A$ e i ponto final $B$, então \[ \int_C \mathbf{F} \cdot d\mathbf{s} = f(B) - f(A) \nonumber \] |
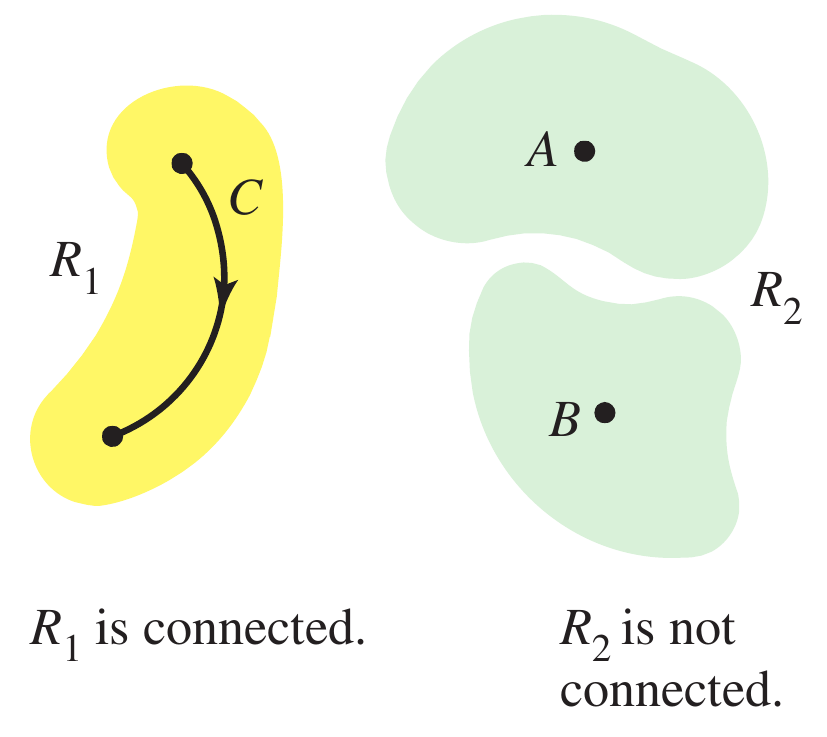
Só para lembrar que um espaço $R$ é dito conexo se dois pontos quais quer dentro de esse espaço podem ser ligado mediante uma caminho o qual tem a sua imagem definida em $R$
Da definição acima vemos que qualquer campo conservativo ($\vec{\nabla} \times \mathbf{F} = 0$ e simplesmente conexo) tem a sua integral de linha independente do caminho de integração.