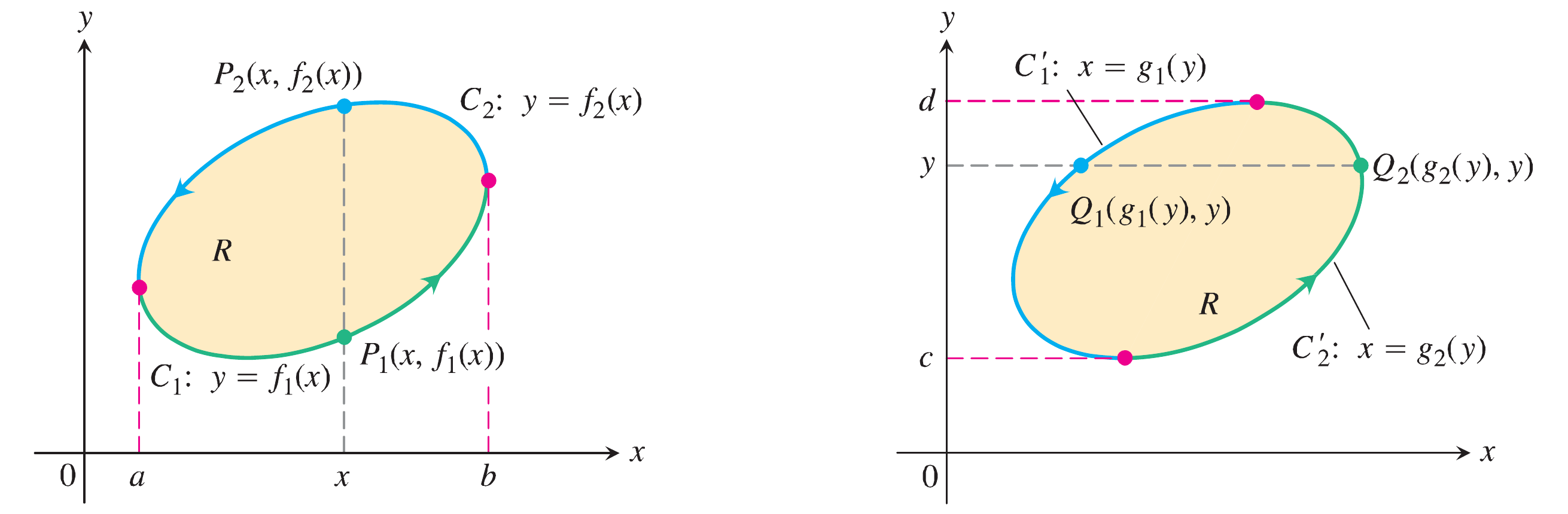O teorema de Green

Este teorema é o primeiro de três teoremas (relacionados) que amaram o cálculo vetorial diferencia e o cálculo vetorial integral. Além da sua importância intrínseca à matemática, especificamente à topologia, eles são teoremas fundamentais a serem utilizados em aplicações física, por exemplo, o teorema de Green, descoberto em 1828, aparece na teoria de potenciais (aqui se incluí os potenciais gravitacionais e elétricos); o teorema de Gauss-Ostrogradsky (ou teorema da divergência), aparece no estudo de capilaridade; o teorema de Stokes aparece na dinâmica dos fluídos e eletromagnetismo.

Antes de entrar nas especifidades do teorema devo mencionar que este teorema é uma generalização do II teorema fundamental do cálculo. O II teorema fundamental do cálculo afirma \[ \int_a^b \dfrac{\;}{dx}\,f(x)\,dx = f(b) - f(a) \nonumber \] que a integral da derivada de uma função de uma variável, calculada num intervalo $[a,\,b]$, está dada pela diferença dos valores que a função assume na fronteira do intervalo de integração.

Similarmente vimos que a integral de linha de um campo vetorial, para o caso de um campo conservativo, também é uma outra expressão similar ao teorema fundamental do cálculo, para esses casos se obtém que \[ \int_C \mathbf{F}\cdot d\mathbf{s} = f(B) - f(A) \nonumber \] onde \[ \mathbf{F} = \vec{\nabla}\,f \nonumber \] desde que $\mathbf{F}$ seja um campo conservativo.

Da mesma forma o teorema de Green é uma releitura do II teorema fundamental do cálculo para o caso de duas dimensões, se consideramos uma função $\mathbf{F}=\mathbf{F}(x,y)$, o teorema de Green relaciona a $\mathbf{k}-$essima componente do rotacional de $\mathbf{F}$ (que é uma derivada que envolve ambas coordenadas), com a integral de linha da componente tangencial de $\mathbf{F}$ ao longo da curva $C$, percorrida em sentido positivo, que limita a região $R$, isto é \[ \begin{array}{rcl} \iint_R \left( \vec{\nabla}\times\mathbf{F} \right) \cdot \mathbf{k} & = & \oint_C \mathbf{F} \cdot d\mathbf{s}\\ \iint_R \left( \dfrac{\partial F_1}{\partial x} - \dfrac{\partial F_2}{\partial y} \right) dxdy &=& \oint_C F_1(x,y)dx+F_2(x,y)dy \end{array} \nonumber \] Note que $C$ é a curva que limita a região $R$ (assim como $a$ e $b$ são os limites do intervalo no caso em que avaliamos a integral tradicional).

Antes de mostrar como o teorema de Green é uma outra forma do teorema fundamental do Cálculo, vamos dar a definição formal do teorema e dar uma demostração desse teorema para um caso bem específico.

Teorema de Green-Ostrogradsky

Seja $D$ uma região fechada definida em $\mathbb{R}^2$ com fronteira $C=\delta D$ a qual é formada por um número finito de curvas simples fechadas seccionalmente continuas, com orientação da curva $C$ definida de forma a ter $D$ sempre à direita enquanto $C$ é percorrida. Seja $\mathbf{F}(x,y) = M(x,y)\,\mathbf{i} + N(x,y) \,\mathbf{j}$ um campo vetorial de classe $C^1$ definido em todo $D$. Então \[ \oint_C Mdx + Ndy = \iint_D \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y} \right)\,dxdy \nonumber \]

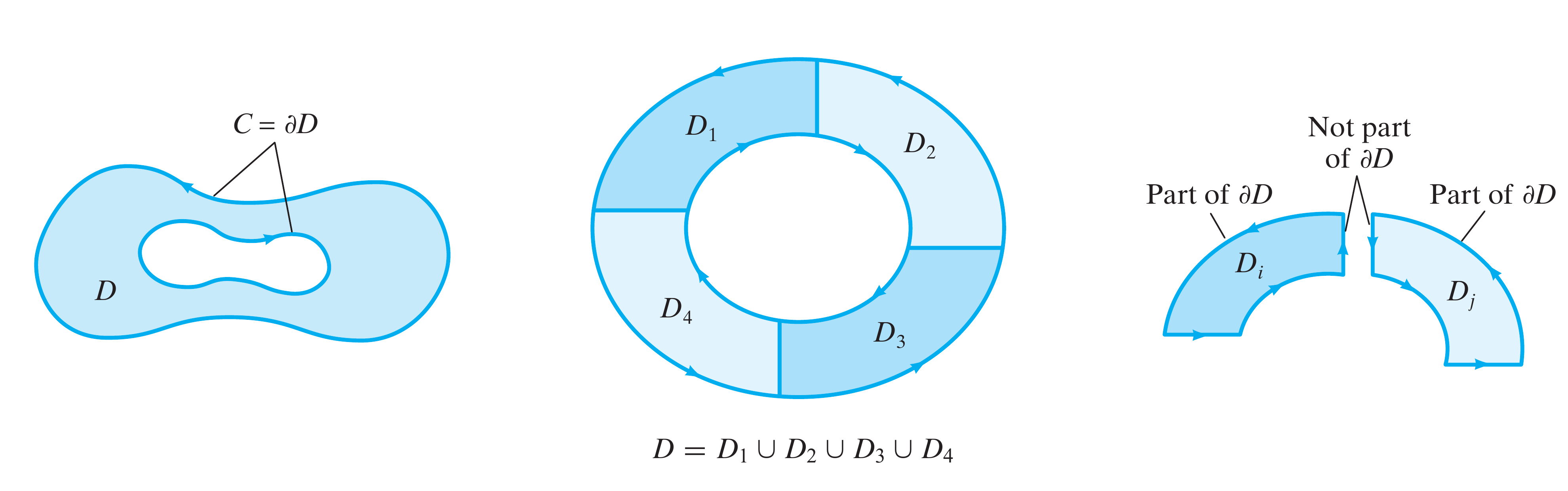
Nessa definição temos algum pontos que devem se ter em conta na hora de aplicar. O primeiro ponto é que nossa superfície pode conter uma quantidade finita de buracos

Como se mostra na figura acima (figura b), redefinindo o caminho de integração transformamos nossa região de integração em duas regiões, $D_1$, $D_2$, $D_3$, e $D_2$, que somadas dão a região original, $D$. O outro ponto a ser considerado é o fato de que a orientação da curva fonteira, $\delta D$, é tal que ao percorrer a curva a região que ela delimita fica sempre à esquerda, como mostra a figura

Um fato histórico curioso é que esse teorema foi proposto pelo matemático auto didata Inglês George Green, Green publicou um livro que posteriormente foi divulgado por Lord Kelvin. Simultaneamente o matemático Russo Mihail Ostrogradsky apresento este teorema.

Vamos apresentar uma verificação da validade do teorema para o caso de superfícies simples, vamos considerar para isso a superfícies definidas na figura embaixo, primeiro consideremos a superfície à esquerda.

Para figura verificamos que a curva $C = \delta R$ resulta da união de duas outras curvas, a curva $C_1$ (parte inferior) e a curva $C_2$ (parte superior), onde \[ C_1: y=f_1(x),\;\;\;a \leq x \leq b,\;\;\;\;\;\;\;\;\;C_2: y=f_2(x),\;\;\;b \geq x \geq a \nonumber \] Consideremos uma função $M$ definida em $R\in \mathbb{R}^2$, derivável. Para essa função (e qualquer outra função similar) se verifica \[ M\left(x,\,f(x)\right) - M\left(x,\,f(x)\right) = \int_{f_1(x)}^{f_2(x)}\,\dfrac{\partial M}{\partial y}\,dy \nonumber \] Essa expressão pode ser integrada em relação a $x$ e entre os limites $a$ e $b$, \[ \begin{align*} \int_a^b \int_{f(x)}^{f(x)}\,\dfrac{\partial f}{\partial y}\,dy\,dx& = \int_a^b \left[ M\left(x,\,f(x)\right) - M\left(x,\,f(x)\right) \right] \,dx\\ &= -\int_b^a M\left(x,\,f(x)\right)\,dx - \int_a^bM\left(x,\,f(x)\right)\,dx \end{align*} \] Observe que podemos pensar a expressão $\displaystyle \int_a^b M\left(x,\,f(x)\right)\,dx$ como sendo a integral de linha do campo escalar $M$ ao longo da cuva parametrizada como $y = f(x)$, sendo $x$ o parâmetro; desde que $\left| \mathbf{v}\right|=1$ (dessa forma parametrizado em termos do comprimento de arco). Uma analise similar pode ser realizada para o termo $\displaystyle \int_b^a M\left(x,\,f(x)\right)\,dx$, de forma que \[ \begin{align*} \int_a^b \int_{f_1(x)}^{f_2(x)}\,\dfrac{\partial M}{\partial y}\,dy\,dx& = -\oint_C M\left(x,\,f(x)\right)\,dx\\ \iint_R\dfrac{\partial M}{\partial y}\,dy\,dx& = -\oint_{\delta R} M\left(x,\,y\right)\,dx \end{align*} \]

Da figura à direita verificamos que a curva $C' = \delta R$ resulta da união de duas outras curvas, a curva $C_1'$ (lado esquerdo) e a curva $C_2'$ (lado direito), onde \[ C_1': x=g_1(y),\;\;\;c \leq y \leq d,\;\;\;\;\;\;\;\;\;C_2: x=g_2(x),\;\;\;d \geq x \geq c \nonumber \] Agora considere a função $N$ definida em $R\in \mathbb{R}^2$, derivável. Para essa função (e qualquer outra função similar) se verifica \[ N\left(g(y),\,y\right) - N\left(g(y),\,y\right) = \int_{g_1(y)}^{g_2(y)}\,\dfrac{\partial N}{\partial x}\,dx \nonumber \] seguindo a metodologia proposta previamente, \[ \begin{align*} \int_c^d \int_{g_1(y)}^{g_2(y)}\,\dfrac{\partial N}{\partial x}\,dx\,dy& = \int_c^d \left[ N\left(g_2(y),\,y\right) - N\left(g_1(y),\,y\right) \right] \,dy\\ & = \int_c^d N\left(g_2(y),\,y\right)\,dy + \int_d^c N\left(g_1(y),\,y\right) \,dy\\ &= \oint_{C'} N\left(x,\,y\right)\,dy \end{align*} \] de forma que \[ \iint_R\dfrac{\partial N}{\partial x}\,dx\,dy = \oint_{\delta R} N\left(x,\,y\right)\,dy \nonumber \] somando ambos resultados obtemos \[ \iint_R \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y} \right)\,dx\,dy = \oint_{\delta R} N\left(x,\,y\right)\,dy + M\left(x,\,y\right)\,dx \nonumber \]

Regiões multiplamente conexas

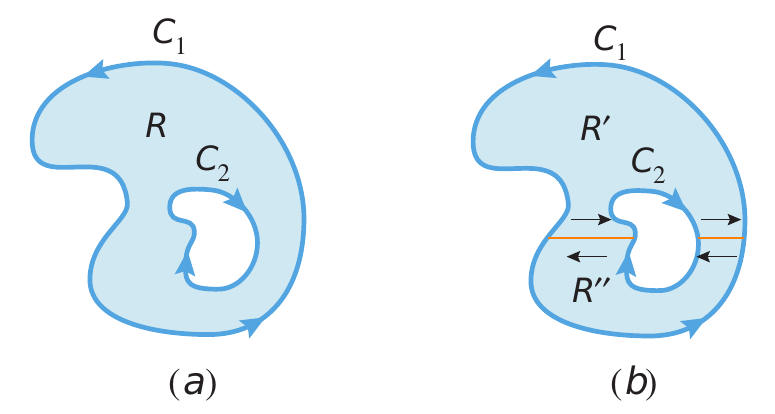
A demonstração previa utilizou-se de um método que é fundamental para a resolução de certo tipo de problemas caraterizados pelo fato de termos um número finito de regiões conexas como as mostradas abaixo

Observe que o nosso objetivo é obter o valor da integral \[ I = \iint_R \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y}\right)dxdy \] como a nossa região é composta por duas regiões então \[ I = \iint_{R'} \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y}\right)dxdy + \iint_{R''} \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y}\right)dxdy \] aplicando green \[ I = \int_{\text{Fronteira de }R'} M(x,y)dx + N(x,y)dy + \int_{\text{Fronteira de }R''} M(x,y)dx + N(x,y)dy \] como ao longo dos cortes (linhas laranjas na figura) a integral referente a $R'$ é percorrida de esquerda para direita e a integral referente a $R''$ é percorrida de direita para esquerda então estas duas integrais se cancelam resultando unicamente em as integrais referentes à curva $C_1$ e $C_2$, isto é \[ \iint_R \left( \dfrac{\partial N}{\partial x} - \dfrac{\partial M}{\partial y}\right)dxdy = \oint_{C_1} M(x,y)dx + N(x,y)dy + \oint_{C_2} M(x,y)dx + N(x,y)dy \] note, no entanto, que a segunda integral é realizada no sentido horário (e não anti horário).

Exemplos