Superfícies paramétricas

Na área anterior utilizamos uma descrição vetorial para definir curvas no espaço $\mathbb{R}^3$. Nesta área vamos tratar de superfícies no espaço, isto é, objetos de dimensão $2$ que habitam $\mathbb{R}^3$

Uma definição precisa de superfície é a seguinte

Definição de superfície

Uma superfície $S$ em $\mathbb{R}^3$ pode ser descrita como um conjunto de pontos $\left( x,y,z \right)$ que satisfaz uma equação da forma \[ f\left( x,y,z \right) = 0 \label{defsup} \] sendo $f$ uma função continua

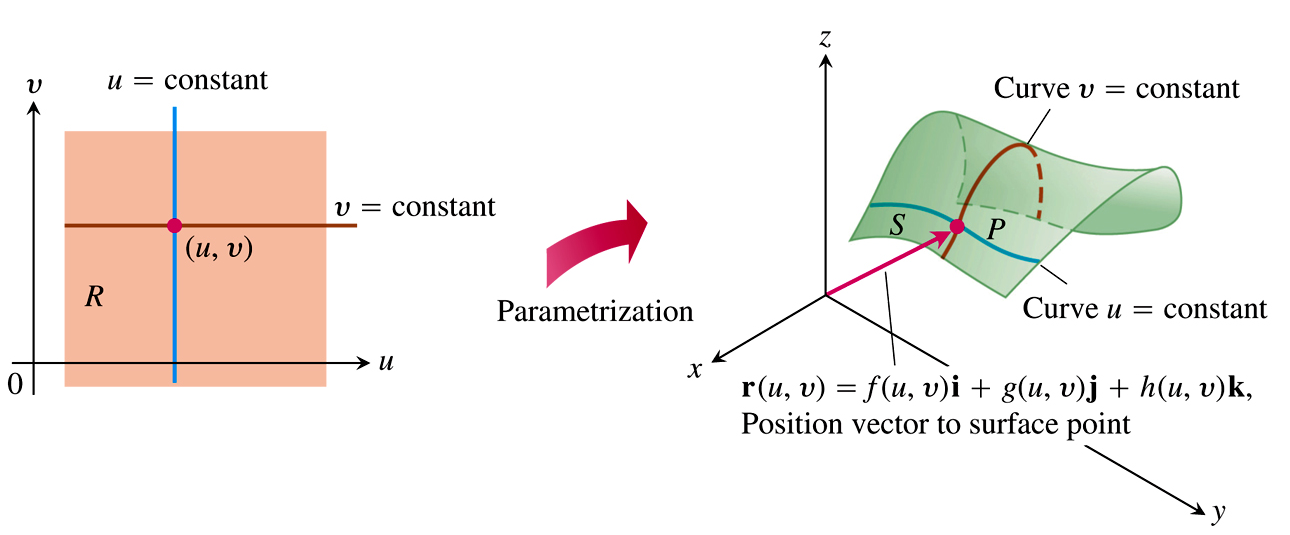
A forma da expressão matemática da equação $\ref{defsup}$ é conhecida como representação implícita da superfície. Se for possível expressar alguma das variáveis em termo das outras variáveis, como em \[ z = f(x,y) \nonumber \] chamaremos a esse tipo de representação de forma explicita da superfície. Veremos mas adiante que é possível localizar os pontos utilizando uma representação vetorial para isso, algo do tipo \[ \mathbf{r}(u,v) = f(u,v)\,\mathbf{i} + g(u,v) \,\mathbf{j} + h(u,v) \,\mathbf{k} \nonumber \] Obviamente podemos ter também uma representação paramétrica constituída pelas componentes do vetor.

A representação paramétrica ou vetorial nos permitira expressar de forma simples equações que nem sempre são funções mas que expressam a superfície $S$, lembre que numa função não podemos ter mais de um ponto $f(\vec{r})$ para um dado $\vec{r}$:

Exemplos

1. A equação \[ x + \dfrac{1}{2}y + \dfrac{1}{3}z = a,\;\;\;a > 0 \nonumber \] é uma representação implicita do plano inclinado que corta os eixos coordenados $x$, $y$, $z$, nos pontos $\left( a,\,0,\,0 \right)$, $\left( 0,\,2a,\,0 \right)$ e $\left( 0,\,0,\,3a \right)$. A partir dessa equação podemos obter uma expressão que seja uma representação explícita desse planos: \[ x = a - \dfrac{1}{2}y - \dfrac{1}{3}z\;\;\;\;\;\text{ ou } \;\;\;\;\; y = 2\left( a - x - \dfrac{1}{3}z \right) ;\;\;\;\;\text{ ou } \;\;\;\;\; z = 3\left( a-x-\dfrac{1}{2}y \right) \nonumber \] Vale ressaltar que cada equação representa toda a superfície, por tanto não temos "perda de informação" quando expressamos explicitamente a função.
2. A equação \[ \displaystyle x^2 + y^2 + z^2 = a^2 \nonumber \] é uma representação implícita da esfera de raio $a$ com centro na origem. Essa equação não é uma função. A partir dessa equação obtemos duas funções que representam parte da diferentes da esfera, \[ z = \sqrt{a^2 - x^2 - y^2}\;\;\;\;\;\text{ e } \;\;\;\;\; z = -\sqrt{a^2 - x^2 - y^2} \nonumber \] Expressões similares podem ser obtidas isolando as outras variáveis. Note que sempre teremos 2 equações para representar
3. A equação \[ x-z+z^3=0 \nonumber \] é uma representação implícita de uma superfície que não pode ser escrita como uma única função, existe até $3$ valores de $z$ para alguns $x$.

Nos exemplos acima vemos que em algumas situações podemos expressar as superfícies de forma funcional, mas em outros não, a pergunta que surge é como representar esses casos de outra forma a fim de ficar simples a construção do gráfico, para isso utilizaremos a representação paramétrica.

Representação paramétrica

Quando estudamos a representação paramétricas das curvas no espaço utilizamos um único parâmetro para isso, dado o fato de que o objeto a ser descrito era em essência unidimensional. No entanto, se queremos parametrizar uma superfície será necessário a utilização de dois parâmetros para identificar cada ponto, já que o objeto a ser descrito é bidimensional.

Definição

Uma parametrização de uma superfície $S \subset \mathbb{R}^3$ é uma função $\displaystyle \mathbf{r}:D\subset \mathbb{R}^2 \to \mathbb{R}^3$, onde $D$ é algum domínio em $\mathbb{R}^2$. A imagem da função $\displaystyle \mathbf{r}$, corresponde à superfície $S$, isto é, $S=Im\left( \mathbf{r} \right)=\mathbf{r}\left( D \right)$. A expressão geral para $\displaystyle \mathbf{r}$ é \[ \mathbf{r}(u,v) = x(u,v) \,\mathbf{i} + y(u,v) \,\mathbf{j} +z(u,v) \,\mathbf{k} \nonumber \] Se $\displaystyle \mathbf{r}$ é diferenciável ou de classe $C^1$ (o que significa que $x(u,v)$, $y(u,v)$ e $z(u,v)$ são diferenciáveis ou de classe $C^1$) então diremos que a superfície é diferenciável ou de classe $C^1$

Representação paramétrica de algumas superfícies

Esfera

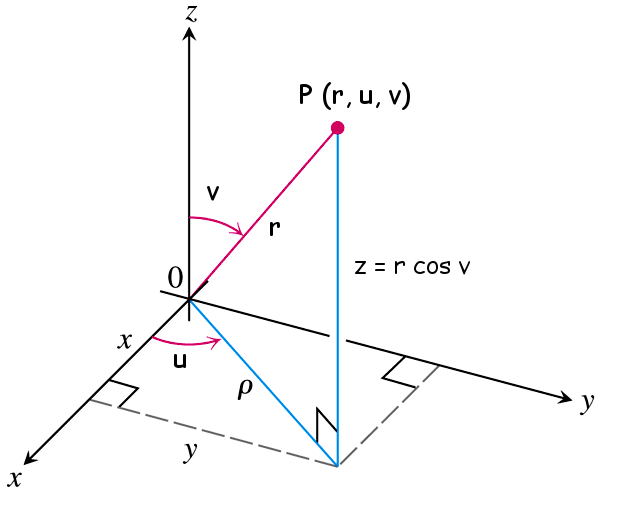
A grande maioria dos autores prefere parametrizar a esfera utilizando coordenas esféricas, $\left(\rho, \phi, \right)$, as quais são facilmente obtidas a partir da figura embaixo

\[ \begin{align*} x =& r \cos \,u\;\sin\, v\\ y =& r \sin \,u\;\sin\, v\\ z =& r \cos\, v \end{align*} \] onde $\displaystyle 0 \leq u \leq 2\pi$ e $\displaystyle 0 \leq v \leq \pi$

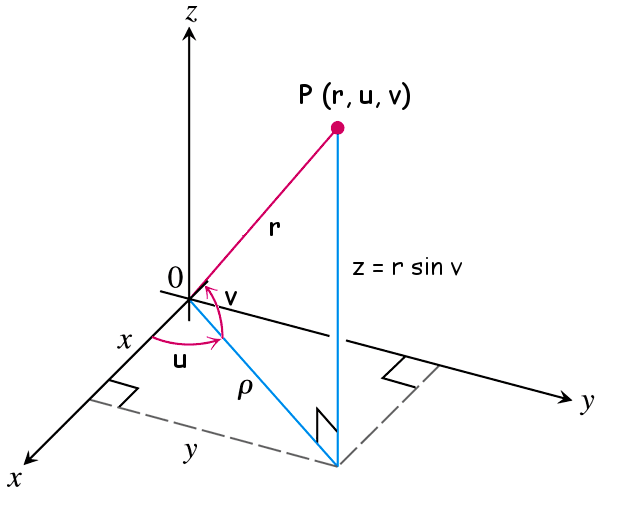
No livro da Diva temos uma outra parametrização alternativa à anterior

\[ \begin{align*} x =& r \cos \,u\;\cos\, v\\ y =& r \sin \,u\;\cos\, v\\ z =& r \sin\, v \end{align*} \] onde $\displaystyle 0 \leq u \leq 2\pi$ e $\displaystyle -\pi/2 \leq v \leq \pi/2$

Exemplos

1. Parametrize $\displaystyle x^2+y^2+z^2=a^2$, que está no primeiro octante.
2. Determine a parametrização de $\displaystyle x^2 + y^2+z^2=16$, para $z \geq 2$
3. Seja $\displaystyle ^2-2x+y^2-4y+z^2+1=0$, encontre uma parametrização.

Parametrização de um cilindro

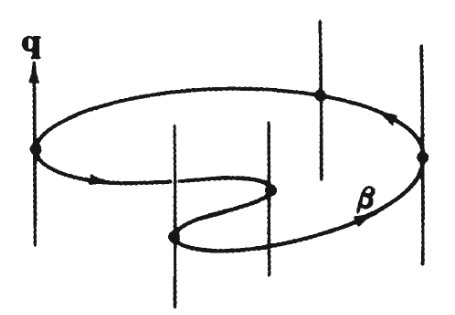
Seja $C$ uma curva plana e $L$ é uma reta que não está situada no mesmo plano da curva $C$. O conjunto de retas paralelas a $L$ que interceptam $C$ é chamado de cilindro.

A curva $C$ é chamada de diretriz e a cada reta que passa por $C$ e é paralela a $L$ é chamada de geratriz do cilindro.

Para parametrizar um cilindro, parametrizamos a curva $C$ utilizando o parâmetro $u$ e as geratrizes são parametrizadas com o parâmetro $v$.

Assim, se $\beta$ é a diretriz e $\mathbf{v}$ é a geratriz, então uma equação geral para um cilindro é \[ \mathbf{r}(u,v) = \beta(u) + v\mathbf{q} \nonumber \] onde $\beta(u)$ é a parametrização da diretriz.

Como exemplo temos o cilindro circular reto, cujas geratrizes são perpendiculares às diretrizes, as quais são círculos. Sabemos que a parametrização do círculo, localizado no plano $xy$, está dada por \[ \mathbf{r}(u) = a\cos \,u\,\mathbf{i} + a\sin\, u \,\mathbf{j} \nonumber \] Para a geratriz podemos considerar o vetor $\mathbf{q}$ que está entre os pontos $P_0=(0,0,1)$ e $P_1=(0,0,2)$, por tanto \[ \mathbf{q} = (0,0,2) - (0,0,1)= (0,0,1) = \mathbf{k} \nonumber \] assim a parametrização do cilindro será \[ \mathbf{r}(u,v) = a\cos \,u\,\mathbf{i} + a\sin\, u \, \mathbf{j} + v\,\mathbf{k} \nonumber \]

Exemplos

1. Obter uma parametrização da parte $x^2+y^2=4$, $0\leq z \leq 5$, delimitada pelos semiplanos $y=x$ e $y=2x$, com $z \geq 0$.
2. Obter uma parametrização do cilindro $x^2+y^2=a^2$
3. Indique um conjunto de eqs. paramétricas do cilindro com diretriz dada por uma elipse.
4. Se a diretriz de um cilindro dado é $y=ax^2$, obter uma parametrização para o cilindro.
5. Se $y=a\sin\, x$, parametrize o cilindro resultante.

Parametrização do Cone generalizado

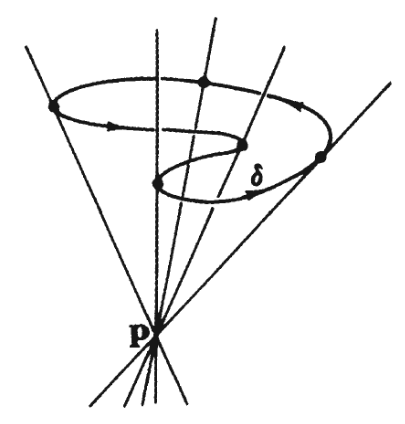
Um cone (generalizado) é uma união de retas passando por um dado ponto $P_0$ (chamado de vértice do cone) e pelos pontos de uma dada curva $\delta$. As retas que passam pelo vértice e pela curva $\delta$ são chamadas de diretrizes e a curva $\delta$ é a geratriz.

Se a geratriz é definida pela curva $\delta(u)$, e o vértice está localizado no ponto $\mathbf{r}_0=(x_0,y_0,z_0)$, então a equação genérica dos cones generalizados tem a forma \[ \mathbf{r}(u,v) = \mathbf{r}_0 + v\, \left( \, \delta(u) - \mathbf{r}_0 \, \right) \nonumber \]

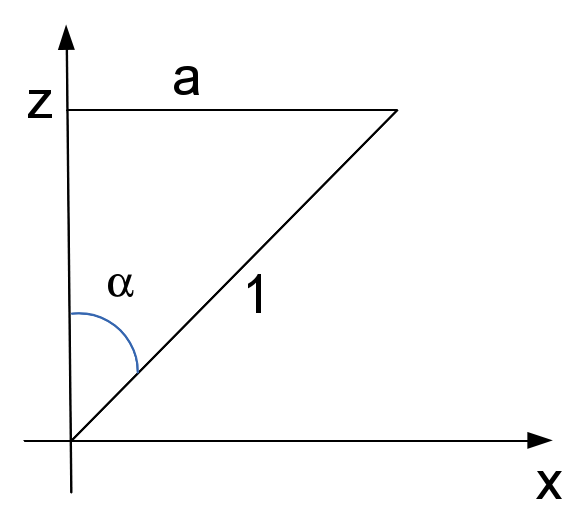
O exemplo mais caraterístico dos cone generalizado é o cone simples: suponhamos que o cone tem seu eixo de simetria ao longo do eixo $z$, nessa circunstância a geratriz está dada pela curva descrita pela equação \[ \mathbf{r}(u) = a\cos \,u\,\mathbf{i} + a\sin\, \,\mathbf{j} + z \,\mathbf{k} \nonumber \] e o vértice está colocado no ponto $\mathbf{r}_0=(0,0,0)$, de forma que a equação genérica para o cone é \[ \mathbf{r}(u,v) = a\,v\,\cos \,u\,\mathbf{i} + a\,v\,\sin\, \,\mathbf{j} + z\,v \,\mathbf{k} \nonumber \] Observe a figura embaixo, a partir dela definimos arbitrariamente como podemos escolher o valor do $z$

Da trigonometria obtemos \[ \sin \alpha = \dfrac{a}{1},\;\;\;\;\;\;\;\;\;\cos \alpha = \dfrac{z}{1} \nonumber \] por tanto, podemos reescreve a equação do cone circular como \[ \mathbf{r}(u,v) = v\,\sin \,\alpha\,\cos \,u\,\mathbf{i} + v\,\sin \,\alpha\,\sin\, \,\mathbf{j} + v\,\cos \,\alpha\, \mathbf{k} \nonumber \]

Vale lembrar que a equação de um cone elíptico está dada por \[ \left( \dfrac{x}{a} \right)^2 + \left( \dfrac{y}{b} \right)^2 = \left( \dfrac{z}{c} \right)^2 \nonumber \]

Exemplo

1. Obter uma parametrização do cone gerado pela semi-reta $z=\sqrt{3}y$, $y>0$, quando está gira em torno do eixo positivo $z$
2. Obter uma parametrização do cone $z=-\sqrt{x^2+y^2}$
3. Obter uma parametrização do cone $4x^2+9z^2=9y^2$
4. Determinar as equações paramétricas do cone $C$ com vértice no ponto $V=(-1,1,1)$ e que tem como diretriz a curva dada por $\displaystyle x^2-4z-4=0$, $y=0$
5. Consideremos a curva de Lissajous, parametrizada por \[ \delta(u) = \left( 4\sin u, 4 \sin \dfrac{u}{4}, 0 \right) \nonumber \] no plano $z=3$ é a diretriz e o ponto $V=(0,0,0)$ é o vértice do cone, indique uma parametrização para o cone.
   

Superfícies de rotação

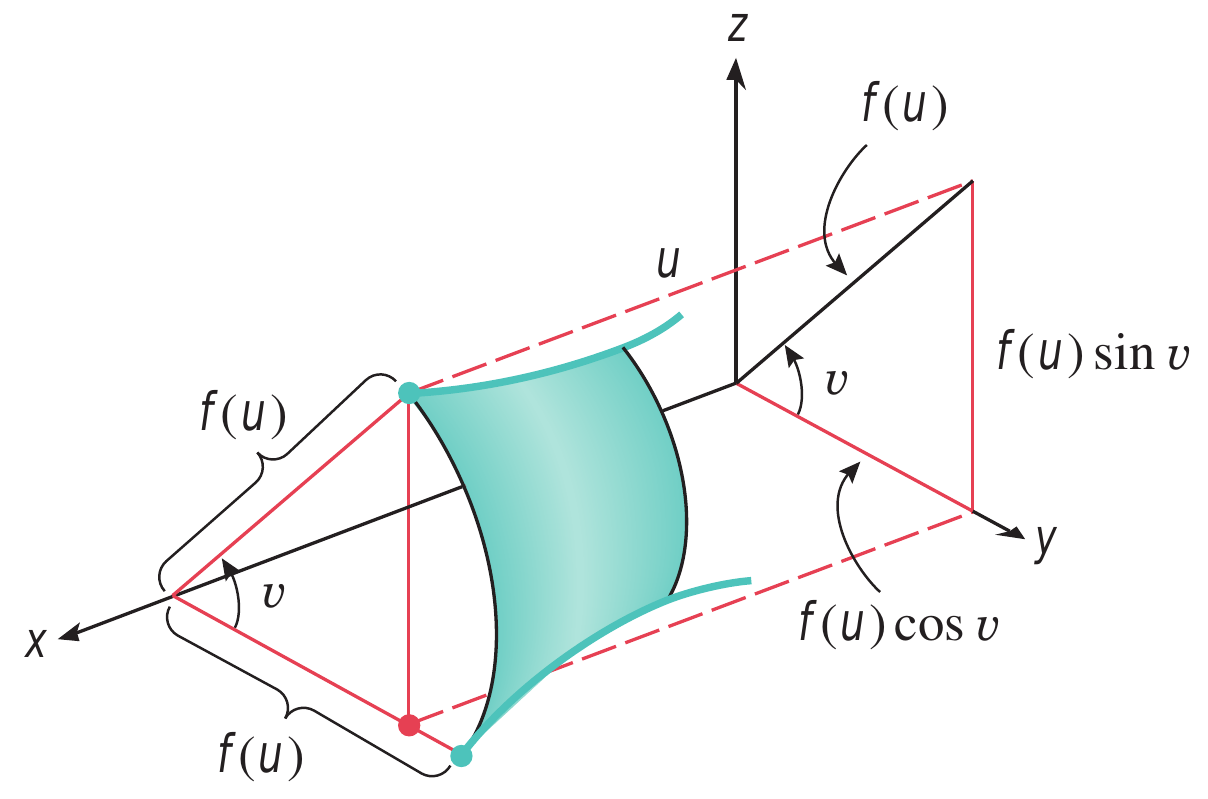
Uma superfície de rotação (ou revolução) é uma superfície obtida pela rotação de uma curva plana, chamada de geratriz, em torno de uma reta nesse plano, a qual chamamos de eixo de rotação. Exemplo dessas superfícies são a esfera, o toro, o paraboloide, o elipsoide (quando dois de seu eixos são iguais), etc.

As circunferências obtidas pela rotação de um ponto fixo da geratriz em torno do eixo de rotação chamam-se paralelos da superfície de rotação e as curvas obtidas pela rotação da geratriz segundo um ângulo fixo chamam-se de meridianos.

Cada ponto $p$ da superfície é obtido pela rotação, de ângulo $v$, de algum ponto $q$ da geratriz. Se a geratriz está dada por $y=f(x)$, então a superfície obtida pela revolução da curva em torno do eixo $x$ está dada por \[ x = u,\;\;\;\;\;\;\;\;\;\;\ y = f(u)\, \cos\, v,\;\;\;\;\;\;\;\;\;\;\ z = f(u)\,\sin\, v \nonumber \]

Exemplos

1. Determine equações paramétricas para a superfície gerada pela revolução da curva $y=1/x$ em torno do eixo $x$
2. Determine equações paramétricas para a superfície gerada pela revolução da curva $y=x$ (cone circular reto)
3. Dada a hipérbole \[ \left(\dfrac{x}{a}\right)^2 - \left(\dfrac{y}{b}\right)^2=0 \nonumber \] expresse de forma paramétrica a superfície resultante da rotação dessa curva em torno eixo $y$.

Paraboloide

A equação cartesiana de uma paraboloide elíptico é \[ \left(\dfrac{x}{a}\right)^2 + \left(\dfrac{y}{b}\right)^2= \dfrac{z}{c'} \nonumber \]

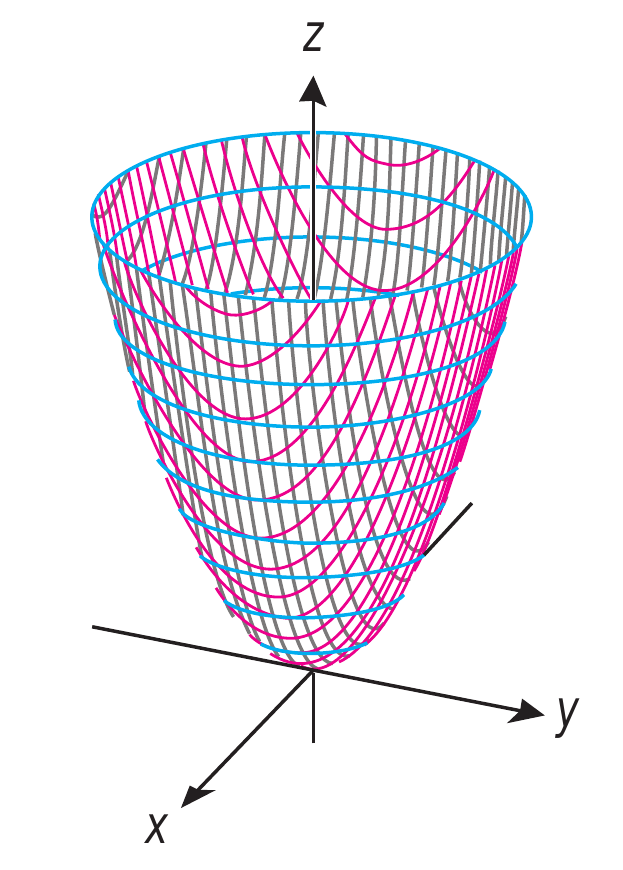
Consideremos o caso especial onde $a=b$ o que resulta em um paraboloide circular \[ z = c\left(x^2 + y^2\right) \nonumber \] Note que se fizermos $y=0$ teremos uma parábola no plano $xz$ dada por $z=cx^2$, similarmente teremos uma parábola no plano $yz$ quando $x=0$, isto é, $z=y^2$.

Mesmo que o paraboloide seja uma superfície de revolução a escolha do eixo de rotação deve ser a adequada. A equação $z=cx^2$ aponta para se escolher $x=u$, similarmente a equação $z=cy^2$ aponta para se escolher $y=u$, contudo nenhuma dessa escolhas é adequada, observe na figura acima, o eixo de rotação é o eixo $z$, por tanto a escolha certa é $z=u$, nesse caso nos não devemos considera as equações anteriores e sim $x = \sqrt{z/c}$ e $y = \sqrt{z/c}$, feita essa escolha nossa seguimos a receita dada para a parametrização de superfícies de revolução \[ \begin{align*} x =& \sqrt{\dfrac{u}{c}}\cos \,v\\ y =& \sqrt{\dfrac{u}{c}}\sin \,v\\ z =& u \end{align*} \] onde $0\leq u < \infty$ e $0\leq v \leq 2\pi$

Parametrização de outras curvas

Quando temos uma superfície definida de forma explica, tipo \[ z = f(x,y) \nonumber \] podemos recorrer à parametrização trivial, isto é, definimos $x=u$ e $y=v$, dessa forma obtemos uma curva superfície definida por $z=f(u,v)$. Um exemplo típico deste fato é o paraboloide o qual está definido de forma explicita \[ z = c\left(x^2 + y^2\right) \nonumber \] e que podemos parametriza como \[ \begin{align*} x =& u\\ y =& v\\ z =& c\left(u^2 + v^2\right) \end{align*} \] neste caso os limites ficam definidos como $u\in \mathbb{R}$ e $v\in \mathbb{R}$.

Sendo mais específicos podemos repetir o exemplo 1 do paraboloide como \[ \begin{align*} x =& u\\ y =& v\\ z =& 2\left(u^2 + v^2\right) \end{align*} \] Como $z_{max} = 8\Rightarrow u^2 + v^2 \leq 8$

Além das superfícies aqui apresentadas podemos explorar a parametrização dos tubos, muito estudada em outras universidades.

Exemplos